Ускорение и СТО

2025-10-08 в 9:19, admin, рубрики: задача, космос, релятивистская кинематика

Многим людям нравится научная фантастика, я тоже люблю иногда почитать "Автостопом по галактике" или посмотреть "Интерстеллар". Во время потребления подобного контента возникает один и тот же вопрос: как они путешествуют на такие далекие расстояния за такое короткое время? Я хочу попробовать ответить на этот вопрос с точки зрения релятивистской механики. В данной статье мы рассмотрим полет ракеты с Земли до ближайшей к Солнцу звезды - Проксиме Центавра.

Условия

В СТО абсолютное большинство задач сводится к задачам с постоянной скоростью, однако для реального мира это будет слишком упрощенная модель, так как чтобы эту скорость набрать, надо для начала двигаться с ускорением. Задача, которую мы рассмотрим сегодня именно про это.

Сразу оговорюсь, что я не буду ставить ограничение на конечную скорость, ракета просто будет постоянно ускоряться. Верхнее ограничение на скорость поставит СТО. Это значит, что в какой-то момент для дальнейшего ускорения нам нужна будет энергия больше той, которая содержится во всей вселенной, но мы закроем глаза на такие мелочи.

Условие: ракета летит с Земли до Проксимы Центавра с нулевой начальной скоростью с ускорением g.
Ускорение возьмем равным 10 м/с
Расстояние между Землей и Проксимой Центавра: световых года или $4,015*10^{13}$ км

Решение задачи

Возьмем систему K, связанную с Землей, и систему K', связанную с ракетой. Мы не можем использовать СТО для случая, когда система отсчета ускоряется, поэтому мы будем брать новую систему K' в каждый момент времени.

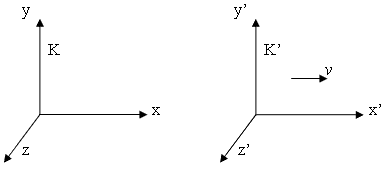
Вывод формулы для скорости

Из преобразований Галилея следует, что в классической механике ускорение не зависит от системы отсчета:

$begin{cases} V'=V-U \ t'=t \ a=frac{dV}{dt}end{cases} Rightarrow a'=a$

В случае релятивистской механики ускорение для разных систем отсчета будет разное. Для системы K' - собственной системы ракеты - ускорение будет равно g:

$frac{dV_x'}{dt}=g$

Найдем, какое ускорение будет в системе K. Выведем это из формулы для сложения скоростей в случае СТО:

$V_x=frac{V_x'+U}{1+frac{V_x'U}{c^2}}Rightarrow dV_x=frac{dV_x'(1+frac{V_x'U}{c^2})-(V_x'+U)frac{U}{c^2}dV_x'}{(1+frac{V_x'U}{c^2})^2}=frac{1-frac{U^2}{c^2}}{(1+frac{V_x'U}{c^2})^2}dV_x'$

Система отсчета K' - система отсчета корабля, значит скорость корабля в этой системе отсчета равна 0:

$begin{cases} dV_x=frac{1-frac{U^2}{c^2}}{(1+frac{V_x'U}{c^2})^2}dV_x'\ V_x'=0end{cases} Rightarrow dV_x=(1-frac{U^2}{c^2})dV_x'$

Выведем формулу для ускорения в лабораторной системе отсчета, используя формулу, полученную выше, и формулу для релятивистского замедления времени:

$begin{cases} dV_x=(1-frac{U^2}{c^2})dV_x'\dt=frac{dt'}{sqrt{1-frac{U^2}{c^2}}}\ frac{dV_x'}{dt}=gend{cases}Rightarrowfrac{dV_x}{dt}=(1-frac{U^2}{c^2})^{frac{3}{2}}frac{dV_x'}{dt'} Rightarrowfrac{dV_x}{dt}=g(1-frac{U^2}{c^2})^{frac{3}{2}}$

Из-за невозможности использования СТО для случая, когда система отсчета ускоряется, мы будем в каждый момент времени брать новую систему отсчета K', связанную с ракетой, поэтому в каждый момент времени будет равно :

$frac{dV_x}{dt}=g(1-frac{U^2}{c^2})^{frac{3}{2}}Rightarrowfrac{dV_x}{dt}=g(1-frac{V_x^2}{c^2})^{frac{3}{2}}$

Получили дифференциальное уравнение. Его можно решить с помощью замены $beta=frac{V_x}{c}$ :

$frac{dbeta}{dt}=frac{g}{c}(1-beta^2)^{frac{3}{2}}Rightarrowfrac{dbeta}{(1-beta^2)^{frac{3}{2}}}=frac{g}{c}dt$

Теперь сделаем еще одну замену, теперь тригонометрическую :

$frac{dbeta}{(1-beta^2)^{frac{3}{2}}}=frac{dsin(tau)}{(1-sin^2(tau))^{3/2}(tau)}=frac{cos(tau)dtau}{(1-sin^2(tau))^{3/2}(tau)}=frac{cos(tau)dtau}{cos^3(tau)}=frac{dtau}{cos^2(tau)}=$ $tg(tau)=sqrt{frac{1}{cos^2(tau)}-1}=sqrt{frac{1}{1-sin^2(tau)}-1}=|sin(tau)=beta|=sqrt{frac{1}{1-beta^2}-1}$

Тогда мы получим следующее уравнение:

$frac{beta}{sqrt{1-beta^2}}=frac{gt}{c}+A$

Подставим начальные условия, чтобы найти константу (в начальный момент времени скорость равна 0):

$frac{0}{sqrt{1-0^2}}=frac{0}{c}+ARightarrow A=0$

Решим такое уравнение, чтобы найти скорость в лабораторной системе отсчета:

$frac{beta}{sqrt{1-beta^2}}=frac{gt}{c}Rightarrowbeta^2(1+(frac{gt}{c})^2)=(frac{gt}{c})^2Rightarrow beta=frac{frac{gt}{c}}{sqrt{1+(frac{gt}{c})^2}}$

Сделаем обратную замену $beta=frac{V_x}{c}$ . Тогда формула для скорости будет выглядеть так:

$V_x=frac{gt}{sqrt{1+(frac{gt}{c})^2}}$

*График зависимости скорости ракеты от времени*

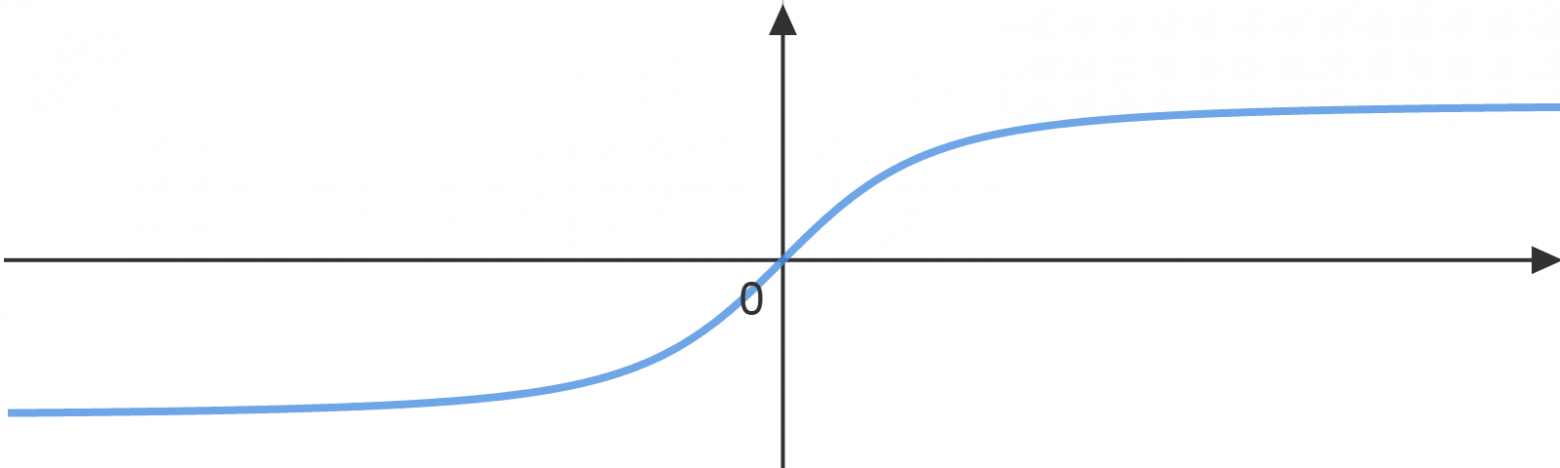
Рассмотрим граничные случаи:

$begin{cases}lim_{trightarrow0}V_x(t)=gt\lim_{trightarrowinfty}V_x(t)=cend{cases}$

В самом начале пути ракета будет двигаться практически по законам классической механики, однако с набором скорости на нее все больше будет действовать релятивистская механика. Если она будет ускоряться бесконечно долго, то ее скорость в лабораторной системе не превысит скорость света, а значит мы не нарушили постулаты СТ.

Вывод формулы для координаты

Найдем зависимость координаты от времени:

$frac{dx}{dt}=V_x(t)=frac{gt}{sqrt{1+(frac{gt}{c})^2}}Rightarrow dx=frac{gt}{sqrt{1+(frac{gt}{c})^2}}dt$ $int dx=int frac{frac{c^2}{g}d(1+(frac{gt}{c})^2)}{sqrt{1+(frac{gt}{c})^2}}Rightarrow x=frac{c^2}{g}sqrt{1+(frac{gt}{c})^2}+A$

Подставим начальные условия, чтобы найти константу (в начальный момент времени координата равна 0):

$0=frac{c^2}{g}sqrt{1+(frac{0}{c})^2}+ARightarrow A=-frac{c^2}{g}$

Таким образом формула для координаты будет выглядеть так:

$x=frac{c^2}{g}sqrt{1+(frac{gt}{c})^2}-frac{c^2}{g}$

Приведем это уравнение к виду, в котором мы сможем определить вид зависимости:

$frac{g^2}{c^4}(x+frac{c^2}{g})^2-t^2frac{g^2}{c^2}=1$

Графиком функции в данном случае будет являться гипербола.

*График зависимости координаты ракеты от времени*

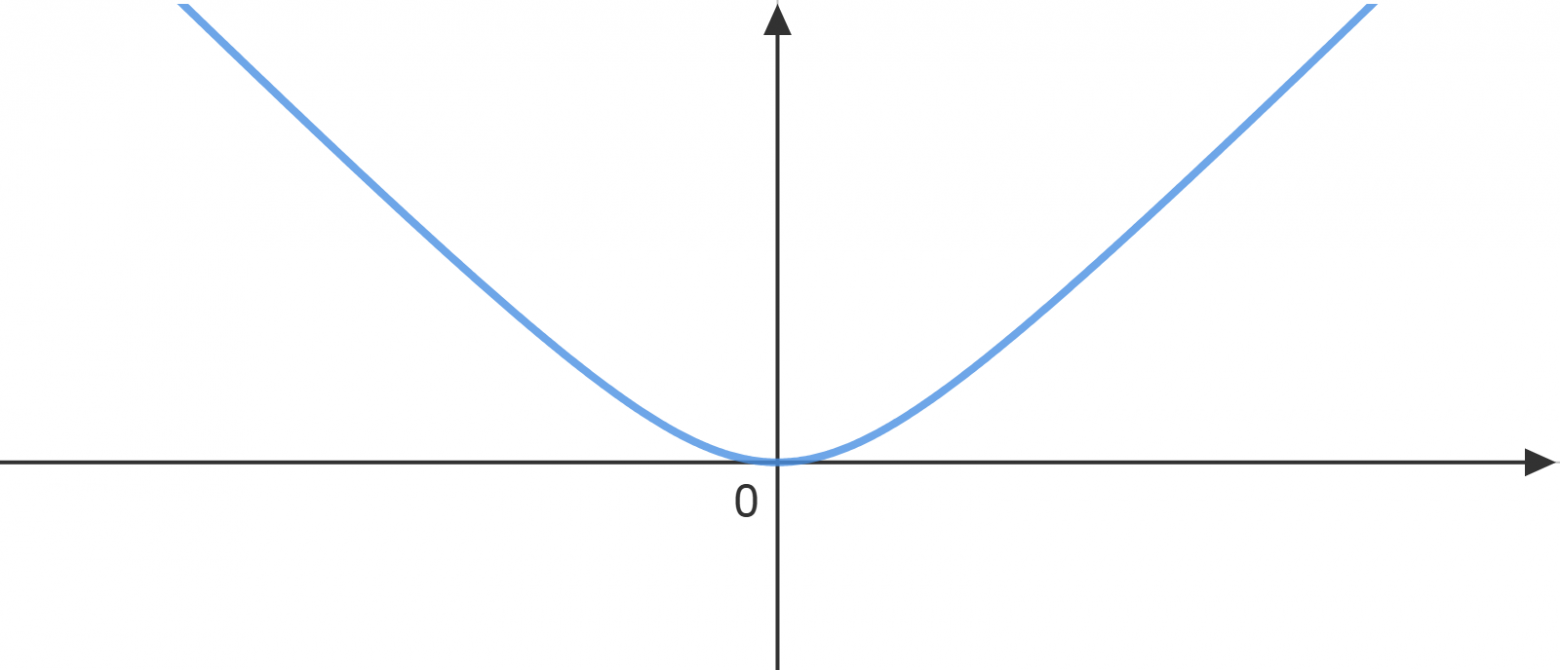
Рассмотрим граничные случаи:

$begin{cases}lim_{trightarrow0}x(t)=frac{gt^2}{2}\lim_{trightarrowinfty}x(t)=ct-frac{c^2}{g}end{cases}$

Координаты также, как и скорость тоже сначала меняется по законам классической механики, а с увеличением скорости увеличивается влияние СТО.

Вывод формулы для времени

Найдем зависимость времени, которое прошло в лабораторной системе отсчета, от пройденного пути.

$c^2t^2=(x+frac{c^2}{g})^2-frac{c^4}{g^2}Rightarrow t=frac{c}{g}sqrt{frac{g^2}{c^4}(x+frac{c^2}{g})^2-1}$

Для того, чтобы найти собственное время, выразим интервал в обеих системах отсчета. При этом , так как ракета не двигается в собственной системе отсчета:

$begin{cases}dS=sqrt{c^2dt^2-dx^2}=cdtsqrt{1-frac{dx^2}{c^2dt^2}}=cdtsqrt{1-frac{V^2}{c^2}}\ dS'=sqrt{c^2dt'^2-dx'^2}=cdt'end{cases}$

Так как интервал - инвариантная величина, и части будут равны:

$cdtsqrt{1-frac{V^2}{c^2}}=dS=dS'=cdt'Rightarrow dt'=sqrt{1-frac{V^2}{c^2}}dt$ $begin{cases} t'=intsqrt{1-frac{V^2}{c^2}}dt \ V_x=frac{gt}{sqrt{1+(frac{gt}{c})^2}}end{cases}Rightarrow t'=intsqrt{1-frac{g^2t^2}{c^2(1+(frac{gt}{c})^2)}}dt=frac{c}{g}intfrac{d(frac{dt}{c})}{sqrt{1+(frac{gt}{c})^2}}$ $t'=frac{c}{g}ln|frac{gt}{c}+sqrt{1+(frac{gt}{c})^2}|+A$

Подставим начальные условия, чтобы найти константу ():

$0=frac{c}{g}ln|frac{0}{c}+sqrt{1+(frac{0}{c})^2}|+A=0+ARightarrow A=0$

Таким образом формула для времени в собственной и лабораторной системе отсчета будет выглядеть так:

$begin{cases} t=frac{c}{g}sqrt{frac{g^2}{c^4}(x+frac{c^2}{g})^2-1} \ t'=frac{c}{g}ln|frac{gt}{c}+sqrt{1+(frac{gt}{c})^2}| end{cases}$

Рассмотрим граничные случаи для и :

$begin{cases} lim_{xrightarrow0}=t(x)lim_{xrightarrow0}t'(x)=0 \ lim_{xrightarrowinfty}t(x)=frac{x}{c} \ lim_{xrightarrowinfty}t'(x)=frac{c}{g}ln|frac{2gt}{c}|=frac{c}{g}ln|frac{2gx}{c^2}|end{cases}$

Время в лабораторной и собственной системе отсчета получилось разное. Посмотрим, насколько оно отличается в случае реального в ближайшее время полета к звезде.

Подстановка значений

Теперь, когда мы знаем все зависимости для скорости и времени, посмотрим, за сколько ракета долетит до ближайшей к Солнцу звезде - Проксиме Центавра.

Сначала найдем время в собственной и лабораторной системе отсчета:

$t=frac{3*10^8}{10}sqrt{frac{10^2}{(3*10^8)^4}(4,015*10^{16}+frac{(3*10^8)^2}{10})^2-1}=5,11text{ года}$ $t'=frac{3*10^8}{10} ln|frac{10*t}{3*10^8}+sqrt{(frac{10*t}{3*10^8})^2+1}|=4,14text{ года}$

Разница между собственным временем и временем в лабораторной системе отсчета составила практически целый год.

Теперь найдем скорость, которую она разовьет при подлете к звезде:

$V_x=frac{gt}{sqrt{1+(frac{gt}{c})^2}}=frac{10*t}{sqrt{1+(frac{10*t}{3*10^8})^2}}=0,98c$

Таким образом, ракета пролетит Проксима Центавру со скоростью, равной 0,98 от скорости света.

Вывод

Специальная теория относительности является незаменимым инструментом для анализа задач, в которых тело движется с релятивистскими скоростями и при этом изменяет свою скорость.

Однако применение СТО в таких сценариях требует особой аккуратности и глубокого понимания ее постулатов, поскольку интуиция, сформированная в рамках классической механики, здесь часто оказывается обманчивой и приводит к принципиальным ошибкам. Вот ключевые моменты, на которые следует обращать внимание:

Отказ от классического правила сложения скоростей. В СТО скорости складываются нелинейно, и простое арифметическое сложение или вычитание недопустимо. Необходимо использовать релятивистскую формулу сложения скоростей, которая гарантирует, что результирующая скорость никогда не превысит скорость света.
Релятивистский импульс и энергия. Второй закон Ньютона в его привычной форме () в СТО не работает. Сила приводит к изменению релятивистского импульса (), где — лоренц-фактор, растущий с увеличением скорости. Это объясняет, почему разогнать массивное тело до скорости света невозможно — потребовалась бы бесконечная энергия (). В нашей задаче мы решили не учитывать это, однако в случае реальных запусков это естественно стоит учесть.
Относительность одновременности и замедление времени. Процессы, происходящие с ускоряющимся объектом (например, ход часов в его системе отсчета), с точки зрения неподвижного наблюдателя будут замедляться. Это не абстрактный эффект, а реальное физическое явление, которое необходимо учитывать, например, при расчете времени жизни быстро движущихся частиц.
Корректный выбор системы отсчета. Анализ задачи кардинально меняется в зависимости от того, с точки зрения какой инерциальной системы отсчета он проводится. Часто для решения задачи, связанной с ускорением, используется метод мгновенно сопутствующей инерциальной системы отсчета, которая в каждый момент времени движется с той же скоростью, что и ускоряющееся тело. Только такой тщательный и осознанный подход позволяет успешно применять мощный математический аппарат СТО для решения нестандартных задач в области релятивистской кинематики и динамики.

В данной статье мы разобрали только простейший случай - бесконечное ускорение, которое не соответствует реальности из-за очень большого количества энергии, необходимого для такого ускорения. В дальнейшем можно ввести изменение ускорения с изменением скорости, потому что в каждый момент времени дальнейшее ускорение будет требовать все больше энергии. Ну и конечно стоит рассмотреть замедление в какой-то момент времени, чтобы не просто пролететь какую-то звездную систему, а сесть на планету и т.д.

Пишите в комментариях, если хотите разбор такой задачи, и предлагайте свои решения.

Подготовлено сообществом

Автор: izuuuuuum

Источник