Из квантовой механики в гидродинамику

2025-09-22 в 16:50, admin, рубрики: гидродинамика, квантовая механика, потенциал Бома, система Моделунга, уравнение навье-стокса, уравнение Шрёдингера

Здравствуйте, дорогие друзья! Иногда в голову приходят интересные идеи. Например, можно ли свести уравнение Шрёдингера к чему-то другому, уже известному нам? Оказалось - да!

И вариантов таких преобразований безумно много, но сегодня мы остановимся на одном конкретном. Звучит безумно, но оказывается, уравнение Шрёдингера эквивалентно уравнению Навье-Стокса. И сейчас вы увидите, как перейти от одного к другому.

Переход от Шредингера к Навье-Стоксу

Ну, во-первых, запишем наше любимое уравнение Шрёдингера:

$i hbar frac{partialPsi}{partial t}=-frac{hbar^2}{m}Delta Psi + UPsi$

Думаю, что наши читатели и так знают, что в нём к чему, но для новичков поясню: первое слагаемое - это эволюция состояния во времени, второе отвечает за импульс, а третье - за потенциальную энергию.

Ну и никто нам не запретит переписать комплексную функцию в виде амплитуды и фазы. Тут любители калибровок уже понимают, к чему я веду.

$Psi=A(vec{r})e^{iPhi (vec{r})}$

- это уже вещественная функция амплитуды, а - отвечает за фазу функции.
Подставим этот вид в уравнение Шрёдингера, для этого вычислим производные:

$frac{partialPsi}{partial t}=left(frac{partial A}{partial t} + i Afrac{partialPhi}{partial t}right)e^{iPhi}$

Градиент и лапласиан:

$nablaPsi=big(nabla A + i AnablaPhibig)e^{iPhi}$ $DeltaPsi=e^{iPhi}Big(Delta A + 2inabla AcdotnablaPhi + i ADeltaPhi - A(nablaPhi)^2Big)$

Подставляем в уравнение и сокращаем общий множитель $e^{iPhi}$ .
Подстановка даёт:

$ihbarBig(frac{partial A}{partial t} + i Afrac{partialPhi}{partial t}Big)=-frac{hbar^2}{2m}Big(Delta A + 2inabla A!cdot!nablaPhi + i ADeltaPhi - A(nablaPhi)^2Big) + U A$

Мнимая часть - уравнение непрерывности

Равенство мнимых частей даёт:

$hbarfrac{partial A}{partial t}=-frac{hbar^2}{2m}Big(2nabla AcdotnablaPhi + ADeltaPhiBig)$

Умножаем на и используем :

$frac{partialrho}{partial t}=-frac{hbar}{m}left(nablarhocdotnablaPhi + rhoDeltaPhiright)=-frac{hbar}{m}nablacdot(rhonablaPhi)$

Определим скорость как:

$mathbf v=frac{hbar}{m}nablaPhi$

Получаем уравнение непрерывности:

$frac{partialrho}{partial t} + nablacdot(rhomathbf v)=0$

Действительная часть квантовое уравнение Гамильтона–Якоби

Сравниваем действительные части:

$-hbarfrac{partialPhi}{partial t}=-frac{hbar^2}{2m}frac{Delta A}{A} + frac{hbar^2}{2m}(nablaPhi)^2 + U$

Введём , тогда :

$-frac{partial S}{partial t}=-frac{hbar^2}{2m}frac{Delta A}{A} + frac{1}{2m}(nabla S)^2 + U$

Выделим квантовый потенциал, он называется потенциалом Бома:

$Q=-frac{hbar^2}{2m}frac{Delta A}{A}=-frac{hbar^2}{2m}frac{Deltasqrt{rho}}{sqrt{rho}}$

Итоговое уравнение:

$frac{partial S}{partial t} + frac{(nabla S)^2}{2m} + U + Q=0$

Уравнение Эйлера для скорости

Берём градиент:

$mleft(frac{partialmathbf v}{partial t} + (mathbf vcdotnabla)mathbf vright) + nabla U + nabla Q=0$

Разделим на :

$frac{partialmathbf v}{partial t} + (mathbf vcdotnabla)mathbf v=-frac{1}{m}nabla U - frac{1}{m}nabla Q$

Подставим :

$frac{partialmathbf v}{partial t} + (mathbf vcdotnabla)mathbf v=-frac{1}{m}nabla U + frac{hbar^2}{2m^2}nablaleft(frac{Deltasqrt{rho}}{sqrt{rho}}right)$

Система Маделунга

Мы получили Систему Маделунга — это эквивалентная форма уравнения Шрёдингера, записанная через:

- плотность вероятности (как плотность жидкости).
$mathbf v=frac{hbar}{m}nablaPhi$ - поле скорости «квантовой жидкости».
- квантовый потенциал, порождающий интерференцию, туннелирование и другие квантовые эффекты.

Уравнение Шрёдингера превращается в систему уравнений гидродинамического типа:

$begin{aligned} &frac{partialrho}{partial t} + nablacdot(rhomathbf v)=0,\[6pt] &frac{partialmathbf v}{partial t} + (mathbf vcdotnabla)mathbf v=-frac{1}{m}nabla U + frac{hbar^2}{2m^2}nablaleft(frac{Deltasqrt{rho}}{sqrt{rho}}right). end{aligned}$

Левая часть второго уравнения — так называемая конвективная производная:

$frac{Dmathbf v}{Dt}=frac{partialmathbf v}{partial t} + (mathbf vcdotnabla)mathbf v$

Она описывает перенос не только за счёт конвекции, но и за счёт переноса массы жидкости, а градиент в правой части нужно сначала скалярно умножить на вектор перед применением - и получится новый оператор с разным весом в разные направления.

Сравнение с уравнением Навье–Стокса

Уравнение Навье–Стокса для сжимаемой жидкости:

$frac{partialmathbf v}{partial t} + (mathbf vcdotnabla)mathbf v=-frac{1}{rho}nabla p + nuDeltamathbf v + mathbf f$

, где: - давление, - коэффициент вязкости, - внешние силы.

Сходство:

В системе Маделунга роль давления играет градиент квантового потенциала .
В отличие от классической жидкости здесь нет вязкости (), поток идеален.
Появляется чисто квантовая нелинейная «добавка» , связанная с кривизной плотности вероятности.

Дискретная форма

Переходим от полей к дискретным частицам с индексами и траекториями $vec{r}_n(t)$ :

$vec{v}_n(t)=vec{v}(vec{r}_n, t)$

Уравнения для частиц:

$frac{dvec{v}_n}{dt}=-frac{1}{m}nabla U + frac{hbar^2}{2m^2}nablaleft(frac{Deltasqrt{rho}}{sqrt{rho}}right)Bigg|_{vec{r}=vec{r}_n}$

Плотность вдоль траектории изменяется как:

$frac{drho_n}{dt}=-rho_nnablacdotvec{v}Big|_{vec{r}=vec{r}_n}$

Мы получили лагранжевую систему, где частицы движутся по полю скоростей.

Это не просто красивая аналогия, она позволяет:

Моделирования токов электронов в транзисторах, где поток электронов можно рассматривать как квантовую жидкость. В нанотранзисторах волновая природа тока критична. Система Маделунга позволяет описывать транспорт электронов на уровне плотности и скорости без решения всей квантовой задачи напрямую.
Дает возможность комбинировать с методами молекулярной динамики.

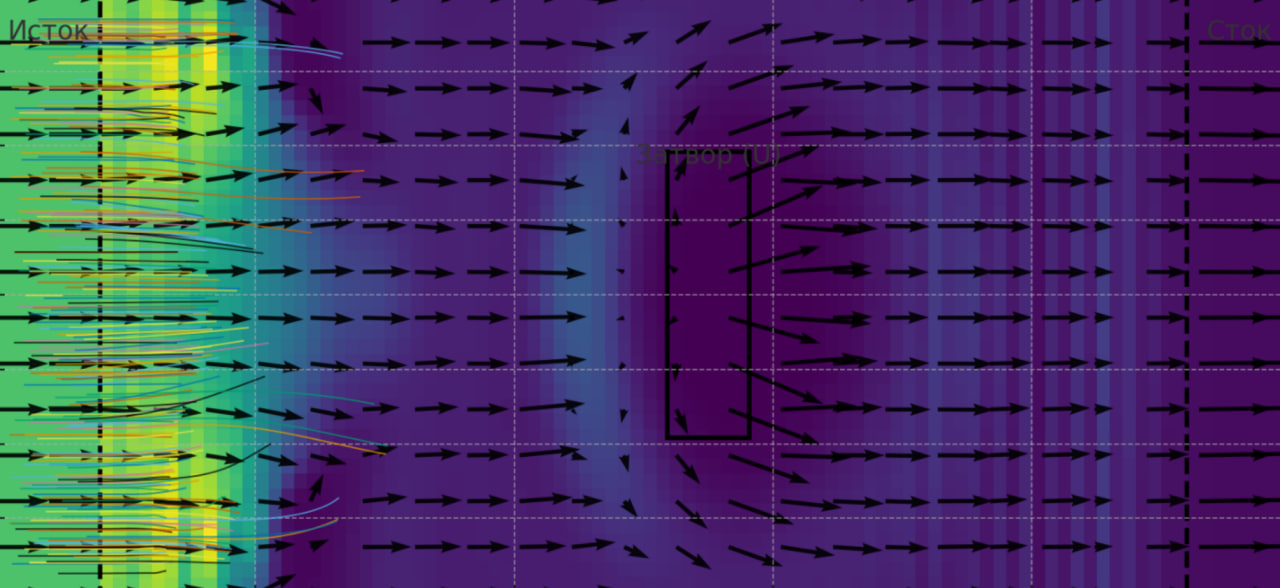
Пример симуляции течения электронов в транзисторе с помощью этой системы

Применение в компьютерной графике

В статье Гидродинамика Шрёдингера на пальцах показано, что систему Маделунга можно использовать для симуляции потоков жидкости в графике игр и фильмов:

Волновая функция дискретизируется на сетке.
Решение уравнения Шрёдингера на шаг времени даёт эволюцию плотности.
Интерференция и вихри появляются автоматически, без ручной настройки.

Визуализация данного метода

Заключение

Мы начали с простого вопроса: можно ли переписать квантовую механику так, чтобы она выглядела как классическая гидродинамика? И шаг за шагом увидели, что уравнение Шрёдингера в полярной форме действительно приводит нас к системе, формально эквивалентной уравнениям Навье–Стокса для идеальной жидкости. При этом привычная волновая функция распадается на плотность и фазу, а квантовые эффекты аккуратно прячутся в виде «квантового потенциала».

Эта формулировка не просто красива математически — она открывает дорогу к практическому применению. И всё это — результат одного аккуратного преобразования.

Так что, возможно, квантовая механика и не так уж далека от классической физики, просто смотреть на неё нужно под другим углом.

P.S. Перед публикацией статьи, увидел на Хабре шикарную статью с похожей темой, всем, кто захотел больше практических примеров, советую ознакомиться.

Кстати если хотите увидеть как перейти от уравнения Шредингера к уравнению Ньютона, пишите в комментариях, может напишу и про это.

Подготовлено сообществом

Автор: LeonidBad

Источник