Математика даёт нам точное представление о почти точных ответах

Используя плотную бумагу и прозрачную ленту, Крэйг Каплан собирает красивый округлый объект, напоминающей творение Бакминстера Фуллера или модный новый тип футбольного мяча. Он состоит из четырёх правильных додекагонов (12-угольников с одинаковыми углами и сторонами) и 12 декагонов (10-сторонних многогранников) с 28 небольшими проёмами в виде равносторонних треугольников. Есть только одна проблема – эта фигура не может существовать. Такой набор полигонов не совпадёт вершинами, и фигура не закроется.
Модель Каплана работает лишь потому, что когда вы собираете её из бумаги, у вас есть небольшая свобода манёвра. Стороны могут почти незаметно изгибаться. «Запас на ошибку, возникающий из-за работы в реальном мире с бумагой, означает, что те вещи, которые не должны быть возможными, в реальности получаются», – говорит Каплан, специалист по информатике из Университета Ватерлоо в Канаде.

Это новый пример из класса неожиданных математических объектов, на которые в 1960-х случайно наткнулся американский математик Норман Джонсон. Джонсон работал над завершением проекта, начатого более 2000 лет назад Платоном – он создавал каталог идеальных геометрических фигур. Из всего бесконечного многообразия трёхмерных фигур только пять можно создать из одинаковых правильных многоугольников: тетраэдр, октаэдр, гексаэдр, икосаэдр, додекаэдр. Если смешать различные правильные многоугольники, можно составить ещё 13 фигур, в которых все многоугольники встречаются вершинами – архимедовы тела – а также призмы (два одинаковых многоугольника, соединённые квадратами) и «антипризмы» (два одинаковых многоугольника, соединённые равносторонними треугольниками).
В 1966 году Джонсон, работая в Университете штата Мичиган, обнаружил ещё 92 тела, состоящих только из правильных многоугольников, которые сейчас [в США] называют джонсоновыми телами. И это исчерпало все возможности, что доказал несолькими годами позже русский математик Виктор Абрамович Залгаллер, работавший тогда в Ленинградском государственном университете. Никакую другую закрытую фигуру из правильных многоугольников составить невозможно.
Но во время инвентаризации многогранников Джонсон заметил нечто странное. Он находил свои формы, составляя их модели из картона и резинок. Поскольку возможных многогранников довольно мало, он ожидал, что новые формы проявятся довольно быстро. Если начать составлять грани вместе, то фигура обязательно должна совпасть. Но этого не происходило. «При сборке кучи многоугольников было не всегда очевидно, собрал ли я допустимую фигуру», – вспоминает Джонсон.
Может казаться, что модель собралась, но «если провести подсчёты, оказывается, что это не совсем так», – говорит он. При тщательном изучении оказывалось, что то, что казалось квадратом, было не совсем квадратом, или стороны были не совсем плоскими. Можно было бы слегка подрезать грани, и они совпали бы идеально, но тогда это были бы уже не правильные многоугольники.
Вознамерившись подсчитать все идеальные фигуры, Джонсон не придавал значения таким «близким попаданиям». «Я отложил их, и сконцентрировался на допустимых», – говорит он. Но эти почти идеальные фигуры не только привлекли внимание Каплана и других любителей математики, они стали частью более крупного раздела почти идеальной математики.
Точного определения «почти точного» попадания не существует. Строгие правила не работают в позволяющем допуски мире. Сейчас Каплан в поиске почти правильных фигур руководствуется приближённым методом: «реальная, математическая ошибка, присущая фигуре, сравнима с практической ошибкой, возникающей из-за работы с материалами реального мира и несовершенными руками». Иначе говоря, если вам удалось собрать невозможный многогранник – если он настолько близок к возможному, что вы можете выдать его за настоящий – тогда это и будет почти точная фигура. В других разделах математики почти точные результаты оказываются так близко к реальным, что могут обмануть или удивить вас – своего рода математическая шутка.
Некоторые такие математические курьёзы нельзя назвать чем-то большим, чем простой забавой, другие же могут иметь глубинные значения в математике и физике.
Древние задачи квадратуры круга и удвоения куба попадают в категорию почти правильных решений. Они кажутся соблазнительно открытыми для нахождения правильного решения, но в итоге оказываются невозможными – как геометрическая фигура, которая выглядит закрытой, но ею не является. Некоторые конструкции, нарисованные Леонардо да Винчи и Альбрехтом Дюрером, слегка искривляли углы, выдавая почти правильные пятиугольники за настоящие.
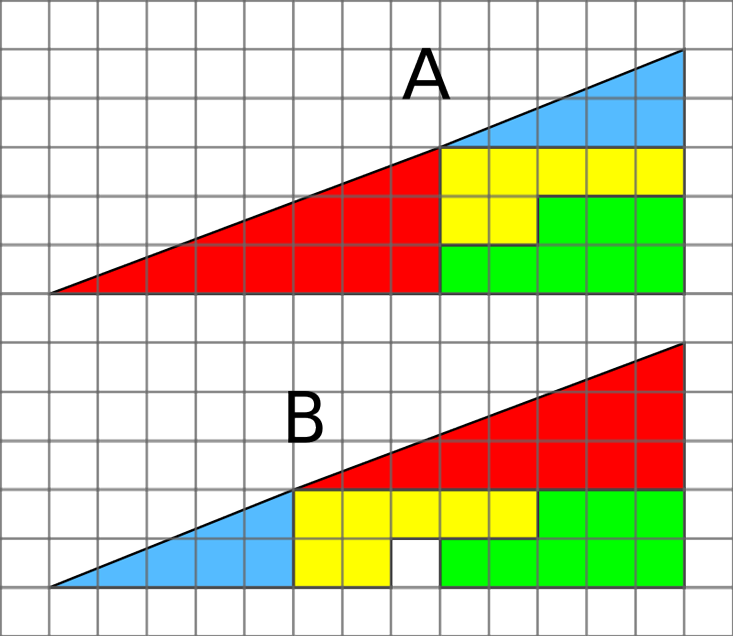
А ещё есть загадка с пропавшим квадратом. На рисунке прямоугольный треугольник разрезан на четыре части. Если переставить их местами, в нём появляется разрыв. Откуда он взялся? Это тоже почти правильное решение. Ни один из треугольников на самом деле не треугольник. Их гипотенузы искривлены, и это почти невозможно заметить, из-за чего иллюзия настолько убедительна.
Цифровое совпадение – это одно из самых полезных в обычной жизни почти правильных решений. 27/12 почти равно 3/2. По схожей причине у фортепьяно есть 12 клавиш в октаве и в основе равномерно темперированного строя западной музыки. Это компромисс между двумя самыми важными музыкальными интервалами: октавой (частотой 2:1) и квинтой (частотой 3:2). Численно невозможно разделить октаву так, чтобы все квинты были идеальными. Но можно подойти к этому достаточно близко, разделив октаву на 12 полутонов, семь из которых дадут вам частоту в 1,498. Для большинства людей этого достаточно.
Иногда почти точные попадания возникают в математике так, будто она сама себя обманывает. В эпизоде Симпсонов «Treehouse of Horror VI» интересующиеся математикой зрители заметили нечто необычное: уравнение 178212 + 184112 = 192212. На первый взгляд может показаться, что сценаристы опровергли Великую Теорему Ферма, постулирующую, что у уравнения xn + yn = zn не существует целочисленных решений при n > 2. Если ввести эти числа в карманный калькулятор, результат покажется вам верным. Но если провести вычисления с точностью, недоступной для большинства карманных калькуляторов, окажется, что корень 12 степени от левой части уравнения равен 1921,999999955867 а не 1922, и Ферма может быть спокоен. Удивительно маленький промах – менее, чем на 10 миллионных частей.
Но такие почти точные попадания – не просто шутки. «Те, что более других интригуют меня, это случаи, намекающие на наличие чего-то более значительного», – говорит Джон Баез, математик из Калифорнийского университета в Риверсайде. Таков случай величины, которую иногда называют константой Рамануджана. Это число eπ √163, равное примерно 262 537 412 640 768 743.99999999999925 – удивительно близко к целому. Мы не можем ожидать, что эти три иррациональных числа – e, π, и √163 – каким-то образом скомбинируются и дадут нам рациональное число, не говоря уже о целом. Но есть причина тому, что они так хорошо совпадают. «Это не простое совпадение, о котором мы не имеем понятия, – говорит Баез. – Это ключ к глубинам математики». Точное объяснение довольно сложное, но основывается на том, что 163 – это наибольшее из чисел Хегнера. Экспоненты, связанные с этими числами, очень близки к целым.
Или взять математическую связь, известную как «Гипотеза монструозного вздора» (monstrous moonshine). История такая: в 1978 году математик Джон Маккей сделал насколько тривиальное, настолько же и интересное наблюдение: 196 884 = 196 883 + 1. Первое число было коэффициентом важного полинома, j-инварианта, а второе возникло в связи с огромным математическим объектом из теории групп под названием "Монстр". Многие люди пожали бы плечами и пошли дальше, но это наблюдение заинтересовало многих математиков, решивших изучить его поближе. Они обнаружили связь между двумя вроде бы несвязанными темами: теорией чисел и симметрией групп Монстр. Эта связь может обладать ещё более широкими, пока не открытыми, последствиями для других тем. Физик Эдвард Уиттен считает, что группа Монстр может быть связанной с квантовой гравитацией и структурой пространства-времени.
Математические почти правильные попадания показывают как игривость, так и мощь человеческого подхода к математике. Джонсон, Каплан и другие делали открытия при помощи проб и ошибок – изучая область, как биолог, продирающийся через джунгли в поисках новых видов. Но в математике проще бывает вести систематический поиск. К примеру Джим Макнил, интересующийся математикой в качестве хобби и собирающий коллекцию почти правильных попаданий на своём сайте, и Роберт Уэбб, программист, создали ПО для создания и изучения многогранников.
Почти точные попадания живут на размытой границе между идеалистической, жёсткой математикой и нашими снисходительными и практическими чувствами. Они выворачивают наизнанку логику приближения. Обычно реальный мир считается несовершенной тенью мира Платона. Совершенство лежащей в основе математики теряется при её реализации. Но в случае почти точных попаданий реальный мир – это идеальная тень неидеального мира. Аппроксимация – это «неправильное приближение правильного ответа», говорит Каплан, а «почти точное попадание – это точное представление почти точного ответа».
Таким способом почти точные ответы меняют связь математиков и математических физиков с природой. «Я благодарен за несовершенства реального мира, поскольку они позволяют мне достигать квазиидеала, работая с объектами, по сути своей неидеальными, – говорит Каплан. – Они позволяют мне преодолевать ограничения математики благодаря красоте сломанной реальности».
Автор: SLY_G





