Несколько дней назад я провел онлайн-контест по игре.
В онлайн-контесте приняло участие 1199 человек, а решений набралось больше 5000, среди которых 61 решение — попытки обойти систему с помощью нахождения уязвимостей. Это очень круто, спасибо всем, кто принял участие.
Эта игра представляет собой тип “игр полковника Блотто”. В ней принимают участие два игрока. У каждого одинаковое кол-во ресурсов, которое нужно разместить на поле NxM. Побеждает тот, кто займет больше клеток (т.е. кол-во ваших ресурсов на ней больше, чем у оппонента). Так выглядит условие для нашей задачи
2. Поле игры представляет собой доску размера 3 на 3.
3. Каждый игрок располагает армией в 100 космодесантников.
4. Перед битвой ночью каждая сторона втайне размещает свои отряды произвольным способом на 9-и клетках. На каждую клетку можно поставить любое целое число космодесантников от 0 до 100.
5. Утром начинается сражение за очередную планету. На каждой из 9 клеток побеждает тот игрок, у кого на этой клетке стоит больше астартес. За победу на каждой из 9 клеток дается 1 очко. Если на некоторой клетке стоит одинаковое число, то сражение на этой клетке заканчивается вничью, и оба игрока получают 0,5 очка.
6. Сражение выигрывает тот, кто выиграл больше полей. Если оба игрока выиграли по 4,5 поля, сражение заканчивается вничью.
Когда я запустил этот эксперимент, я еще не знал, что у этой игры нет идеального решения, но благодаря комментариям я смог лучше разобраться в этой теме.
Начнем с победителей этой игры
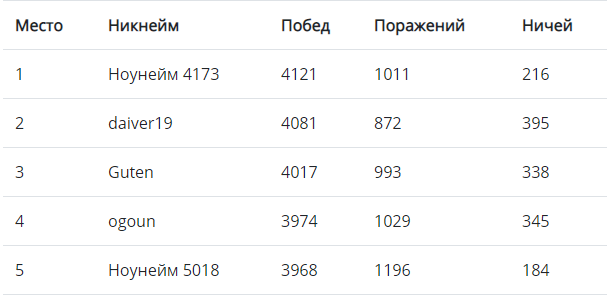
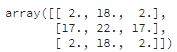
Лучшее решение набрало 4121 побед — весьма неплохой результат. Но что было бы, если бы в игре участвовали решения только из ТОП-100?
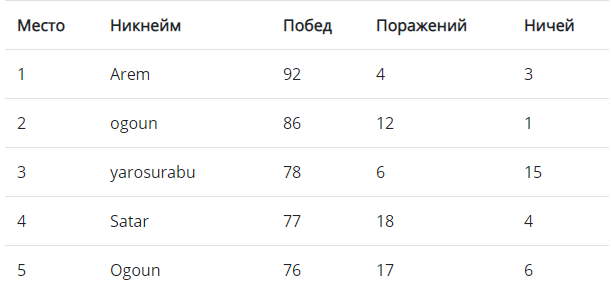
Удивительно, но оно не вошло даже в топ5 (на 8м месте), а 1е место здесь заняло решение с 68-го места.
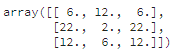
Это как раз показывает, что лучшего решения нет. Остальные результаты можно посмотреть на game.pavlukhinlab.com
Но что еще интересного можно узнать?
Самые большие числа игроки ставили в центр, в среднем все игроки заполняли первую строку большими числами, в то время как лучшие результаты делали больший упор на нижнюю строку.
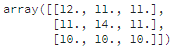

средние значения по всем играм (слева) и по ТОП-100 (справа)
Ну и еще примеры лучших стратегий:
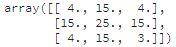
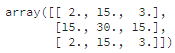
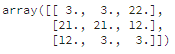
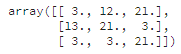
Лучшие стратегии выбирали 5 основных клеток, оставшиеся клетки заполнялись мелкими значениями. Что логично, ведь для победы достаточно занять 5 клеток.
Ну а теперь немного графиков.
Вероятностные распределения чисел:
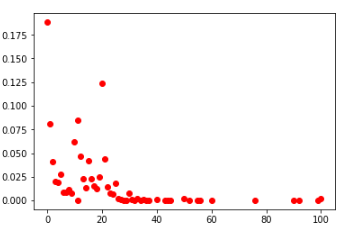
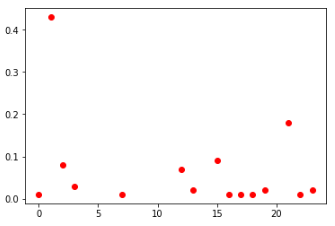
вторые клетки среди всех игроков (слева) и ТОП-100 (справа)
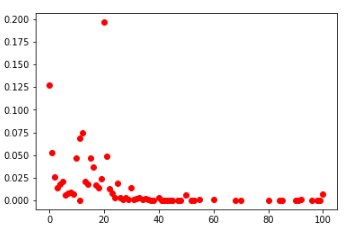
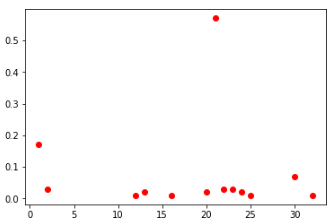
центральные клетки среди всех и ТОП-100
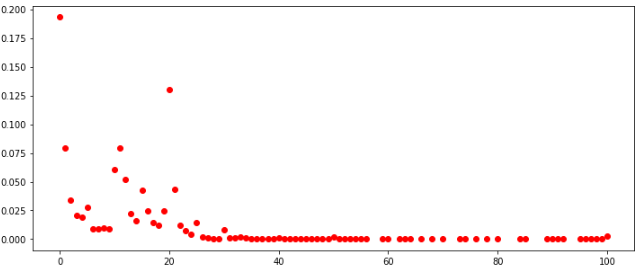
распределение чисел по всем играм
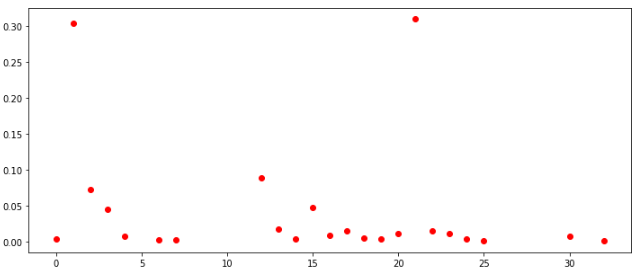
распределение чисел по ТОП-100
Если смотреть распределения по всем клеткам среди всех игроков, то выглядят они в целом похоже. Также можно сделать вывод, что в данных условиях нет смысла заполнять клетки значениями больше 30.
На этом исследование подходит к концу — это все, что я смог извлечь из этих данных. Возможно кто-то из вас сможет предложить что-то еще, что можно проверить — жду вас в комментариях. Обезличенные игры ищите по ссылке.
Пы.Сы. В предыдущем посте я рассказал про нейронку, которая обучалась играть в эту игру. К сожалению, ничего из этого пока не получилось. Две нейронки решили, что лучшая стратегия — кидать нули на выходе и радоваться ничьей. Но может я еще разберусь в этой теме и сделаю отдельный пост посвященный ошибкам, которые я допустил при создании нейронки, и, возможно, успехам.
Автор: Nicknameless