Привет habr.
Тема «магических квадратов» достаточно интересна, т.к. с одной стороны, они известны еще с древности, с другой стороны, вычисление «магического квадрата» даже сегодня представляет собой весьма непростую вычислительную задачу. Напомним, чтобы построить «магический квадрат» NxN, нужно вписать числа 1..N*N так, чтобы сумма его горизонталей, вертикалей и диагоналей была равна одному и тому же числу. Если просто перебрать число всех вариантов расстановки цифр для квадрата 4х4, то получим 16! = 20 922 789 888 000 вариантов.
Подумаем, как это можно сделать более эффективно.

Для начала, повторим условие задачи. Нужно расставить числа в квадрате так, чтобы они не повторялись, и сумма горизонталей, вертикалей и диагоналей была равна одному и тому же числу.
Легко доказать, что эта сумма всегда одинакова, и вычисляется по формуле для любого n:
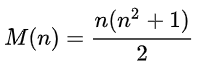
Мы будем рассматривать квадраты 4х4, так что сумма = 34.
Обозначим все переменные черех X, наш квадрат будет иметь такой вид:
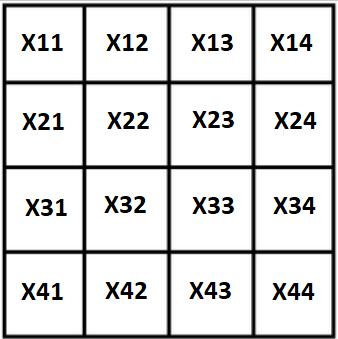
Первое, и очевидное, свойство: т.к. сумма квадрата известна, крайние стоблцы можно выразить через остальные 3:
X14 = S - X11 - X12 - X13
X24 = S - X21 - X22 - X23
...
X41 = S - X11 - X21 - X31
Таким образом, квадрат 4х4 фактически превращается в квадрат 3х3, что уменьшает число вариантов перебора с 16! до 9!, т.е. в 57млн раз. Зная это, приступаем к написанию кода, посмотрим насколько сложен такой перебор для современных компьютеров.
С++ — однопоточный вариант
Принцип программы весьма прост. Берем множество чисел 1..16 и цикл for по этому множеству, это будет х11. Затем берем второе множество, состоящее из первого за исключением числа x11, и так далее.
Примерный вид программы выглядит так:
int squares = 0;
int digits[] = { 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16 };
Set mset(digits, digits + N*N);
for (int x11 = 1; x11 <= MAX; x11++) {
Set set12(mset); set12.erase(x11);
for (SetIterator it12 = set12.begin(); it12 != set12.end(); it12++) {
int x12 = *it12;
Set set13(set12); set13.erase(x12);
for (SetIterator it13 = set13.begin(); it13 != set13.end(); it13++) {
int x13 = *it13;
int x14 = S - x11 - x12 - x13;
if (x14 < 1 || x14 > MAX) continue;
if (x14 == x11 || x14 == x12 || x14 == x13) continue;
...
int sh1 = x11 + x12 + x13 + x14, sh2 = x21 + x22 + x23 + x24, sh3 = x31 + x32 + x33 + x34, sh4 = x41 + x42 + x43 + x44;
int sv1 = x11 + x21 + x31 + x41, sv2 = x12 + x22 + x32 + x42, sv3 = x13 + x23 + x33 + x43, sv4 = x14 + x24 + x34 + x44;
int sd1 = x11 + x22 + x33 + x44, sd2 = x14 + x23 + x32 + x41;
if (sh1 != S || sh2 != S || sh3 != S || sh4 != S || sv1 != S || sv2 != S || sv3 != S || sv4 != S || sd1 != S || sd2 != S)
continue;
// Если числа прошли все проверки на пересечения, то квадрат найден
printf("%d %d %d %d %d %d %d %d %d %d %d %d %d %d %d %dn", x11, x12, x13, x14, x21, x22, x23, x24, x31, x32, x33, x34, x41, x42, x43, x44);
squares++;
}
}
printf("CNT: %dn", squares);
Полный текст программы можно найти под спойлером.
#include <set>
#include <stdio.h>
#include <ctime>
#include "stdafx.h"
typedef std::set<int> Set;
typedef Set::iterator SetIterator;
#define N 4
#define MAX (N*N)
#define S 34
int main(int argc, char *argv[])
{
// x11 x12 x13 x14
// x21 x22 x23 x24
// x31 x32 x33 x34
// x41 x42 x43 x44
const clock_t begin_time = clock();
int squares = 0;
int digits[] = { 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16 };
Set mset(digits, digits + N*N);
for (int x11 = 1; x11 <= MAX; x11++) {
Set set12(mset); set12.erase(x11);
for (SetIterator it12 = set12.begin(); it12 != set12.end(); it12++) {
int x12 = *it12;
Set set13(set12); set13.erase(x12);
for (SetIterator it13 = set13.begin(); it13 != set13.end(); it13++) {
int x13 = *it13;
int x14 = S - x11 - x12 - x13;
if (x14 < 1 || x14 > MAX) continue;
if (x14 == x11 || x14 == x12 || x14 == x13) continue;
Set set21(set13); set21.erase(x13); set21.erase(x14);
for (SetIterator it21 = set21.begin(); it21 != set21.end(); it21++) {
int x21 = *it21;
Set set22(set21); set22.erase(x21);
for (SetIterator it22 = set22.begin(); it22 != set22.end(); it22++) {
int x22 = *it22;
Set set23(set22); set23.erase(x22);
for (SetIterator it23 = set23.begin(); it23 != set23.end(); it23++) {
int x23 = *it23, x24 = S - x21 - x22 - x23;
if (x24 < 1 || x24 > MAX) continue;
if (x24 == x11 || x24 == x12 || x24 == x13 || x24 == x14 || x24 == x21 || x24 == x22 || x24 == x23) continue;
Set set31(set23);
set31.erase(x23); set31.erase(x24);
for (SetIterator it31 = set31.begin(); it31 != set31.end(); it31++) {
int x31 = *it31;
Set set32(set31); set32.erase(x31);
for (SetIterator it32 = set32.begin(); it32 != set32.end(); it32++) {
int x32 = *it32;
Set set33(set32); set33.erase(x32);
for (SetIterator it33 = set33.begin(); it33 != set33.end(); it33++) {
int x33 = *it33, x34 = S - x31 - x32 - x33;
if (x34 < 1 || x34 > MAX) continue;
if (x34 == x11 || x34 == x12 || x34 == x13 || x34 == x14 || x34 == x21 || x34 == x22 || x34 == x23 || x34 == x24 || x34 == x31 || x34 == x32 || x34 == x33) continue;
int x41 = S - x11 - x21 - x31, x42 = S - x12 - x22 - x32, x43 = S - x13 - x23 - x33, x44 = S - x14 - x24 - x34;
if (x41 < 1 || x41 > MAX || x42 < 1 || x42 > MAX || x43 < 1 || x43 > MAX || x44 < 1 || x41 > MAX) continue;
if (x41 == x11 || x41 == x12 || x41 == x13 || x41 == x14 || x41 == x21 || x41 == x22 || x41 == x23 || x41 == x24 ||
x41 == x31 || x41 == x32 || x41 == x33 || x41 == x34)
continue;
if (x42 == x11 || x42 == x12 || x42 == x13 || x42 == x14 || x42 == x21 || x42 == x22 || x42 == x23 || x42 == x24 ||
x42 == x31 || x42 == x32 || x42 == x33 || x42 == x34 || x42 == x41)
continue;
if (x43 == x11 || x43 == x12 || x43 == x13 || x43 == x14 || x43 == x21 || x43 == x22 || x43 == x23 || x43 == x24 ||
x43 == x31 || x43 == x32 || x43 == x33 || x43 == x34 || x43 == x41 || x43 == x42)
continue;
if (x44 == x11 || x44 == x12 || x44 == x13 || x44 == x14 || x44 == x21 || x44 == x22 || x44 == x23 || x44 == x24 ||
x44 == x31 || x44 == x32 || x44 == x33 || x44 == x34 || x44 == x41 || x44 == x42 || x44 == x43)
continue;
int sh1 = x11 + x12 + x13 + x14, sh2 = x21 + x22 + x23 + x24, sh3 = x31 + x32 + x33 + x34, sh4 = x41 + x42 + x43 + x44;
int sv1 = x11 + x21 + x31 + x41, sv2 = x12 + x22 + x32 + x42, sv3 = x13 + x23 + x33 + x43, sv4 = x14 + x24 + x34 + x44;
int sd1 = x11 + x22 + x33 + x44, sd2 = x14 + x23 + x32 + x41;
if (sh1 != S || sh2 != S || sh3 != S || sh4 != S || sv1 != S || sv2 != S || sv3 != S || sv4 != S || sd1 != S || sd2 != S)
continue;
printf("%d %d %d %d %d %d %d %d %d %d %d %d %d %d %d %dn", x11, x12, x13, x14, x21, x22, x23, x24, x31, x32, x33, x34, x41, x42, x43, x44);
squares++;
}
}
}
}
}
}
}
}
}
printf("CNT: %dn", squares);
float diff_t = float(clock() - begin_time)/CLOCKS_PER_SEC;
printf("T = %.2fsn", diff_t);
return 0;
}
Результат: всего было найдено 7040 вариантов «магических квадратов» 4х4, а время поиска составило 102с.

Кстати интересно проверить, есть ли в списке квадратов тот самый, который изображен на гравюре Дюрера. Разумеется есть, т.к. программа выводит все квадраты размерности 4х4:
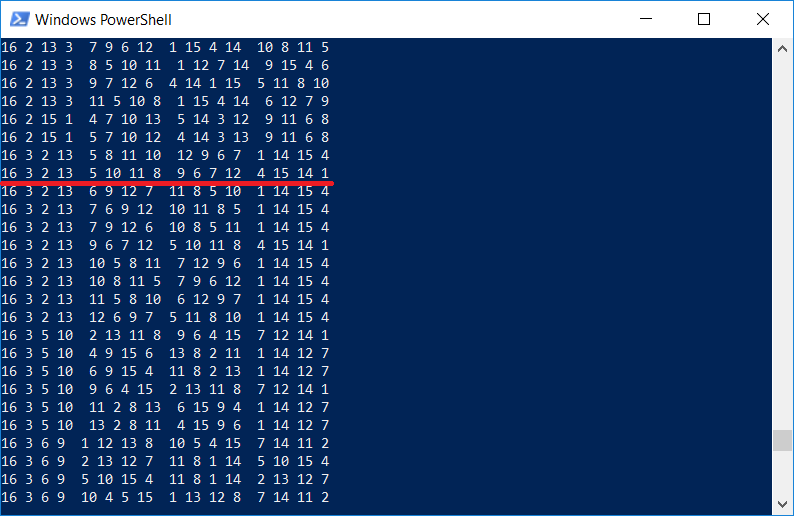
Нельзя не отметить, что Дюрер вставил квадрат в изображение не просто так, цифры 1514 также обозначают год создания гравюры.
Как можно видеть, программа работает (отмечаем задачу как verified at 1514 by Albrecht Dürer;), однако время выполнения не так и мало для компьютера с процессором Core i7. Очевидно, что программа выполняется в один поток, и целесообразно задействовать все остальные ядра.
С++ — многопоточный вариант
Переписать программу с использованием потоков в принципе несложно, хотя и немного громоздко. К счастью, есть почти забытый сегодня вариант — использование поддержки OpenMP (Open Multi-Processing). Эта технология существует аж с 1998г, и позволяет директивами процессора указать компилятору, какие части программы выполнять параллельно. Поддержка OpenMP есть и в Visual Studio, так что для превращения программы в многопоточную, достаточно добавить в код лишь одну строку:
int squares = 0;
#pragma omp parallel for reduction(+: squares)
for (int x11 = 1; x11 <= MAX; x11++) {
...
}
printf("CNT: %dn", squares);
Директива #pragma omp parallel for указывает, что следующий цикл for можно выполнять параллельно, а дополнительный параметр squares задает имя переменной, которая будет общей для параллельных потоков (без этого инкремент работает некорректно).
Результат налицо: время выполнения сократилось со 102с до 18с.
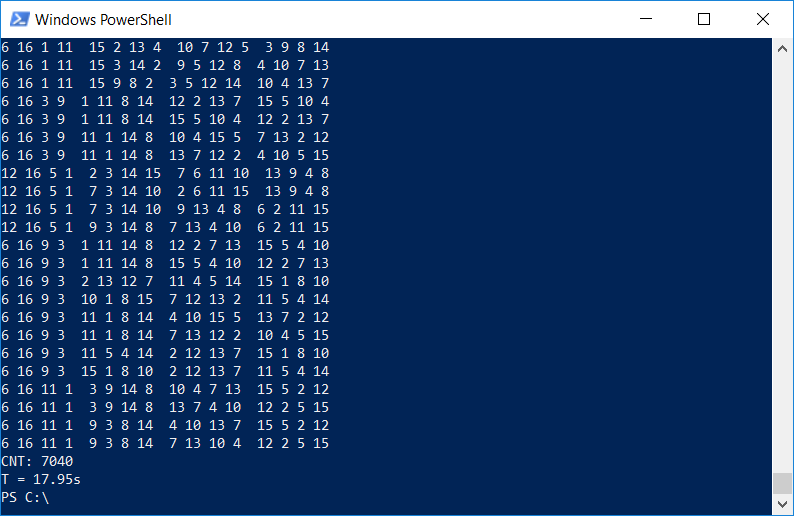
#include <set>
#include <stdio.h>
#include <ctime>
#include "stdafx.h"
typedef std::set<int> Set;
typedef Set::iterator SetIterator;
#define N 4
#define MAX (N*N)
#define S 34
int main(int argc, char *argv[])
{
// x11 x12 x13 x14
// x21 x22 x23 x24
// x31 x32 x33 x34
// x41 x42 x43 x44
const clock_t begin_time = clock();
int squares = 0;
#pragma omp parallel for reduction(+: squares)
for (int x11 = 1; x11 <= MAX; x11++) {
int digits[] = { 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16 };
Set mset(digits, digits + N*N);
Set set12(mset); set12.erase(x11);
for (SetIterator it12 = set12.begin(); it12 != set12.end(); it12++) {
int x12 = *it12;
Set set13(set12); set13.erase(x12);
for (SetIterator it13 = set13.begin(); it13 != set13.end(); it13++) {
int x13 = *it13;
int x14 = S - x11 - x12 - x13;
if (x14 < 1 || x14 > MAX) continue;
if (x14 == x11 || x14 == x12 || x14 == x13) continue;
Set set21(set13); set21.erase(x13); set21.erase(x14);
for (SetIterator it21 = set21.begin(); it21 != set21.end(); it21++) {
int x21 = *it21;
Set set22(set21); set22.erase(x21);
for (SetIterator it22 = set22.begin(); it22 != set22.end(); it22++) {
int x22 = *it22;
Set set23(set22); set23.erase(x22);
for (SetIterator it23 = set23.begin(); it23 != set23.end(); it23++) {
int x23 = *it23, x24 = S - x21 - x22 - x23;
if (x24 < 1 || x24 > MAX) continue;
if (x24 == x11 || x24 == x12 || x24 == x13 || x24 == x14 || x24 == x21 || x24 == x22 || x24 == x23) continue;
Set set31(set23);
set31.erase(x23); set31.erase(x24);
for (SetIterator it31 = set31.begin(); it31 != set31.end(); it31++) {
int x31 = *it31;
Set set32(set31); set32.erase(x31);
for (SetIterator it32 = set32.begin(); it32 != set32.end(); it32++) {
int x32 = *it32;
Set set33(set32); set33.erase(x32);
for (SetIterator it33 = set33.begin(); it33 != set33.end(); it33++) {
int x33 = *it33, x34 = S - x31 - x32 - x33;
if (x34 < 1 || x34 > MAX) continue;
if (x34 == x11 || x34 == x12 || x34 == x13 || x34 == x14 || x34 == x21 || x34 == x22 || x34 == x23 || x34 == x24 || x34 == x31 || x34 == x32 || x34 == x33) continue;
int x41 = S - x11 - x21 - x31, x42 = S - x12 - x22 - x32, x43 = S - x13 - x23 - x33, x44 = S - x14 - x24 - x34;
if (x41 < 1 || x41 > MAX || x42 < 1 || x42 > MAX || x43 < 1 || x43 > MAX || x44 < 1 || x41 > MAX) continue;
if (x41 == x11 || x41 == x12 || x41 == x13 || x41 == x14 || x41 == x21 || x41 == x22 || x41 == x23 || x41 == x24 ||
x41 == x31 || x41 == x32 || x41 == x33 || x41 == x34)
continue;
if (x42 == x11 || x42 == x12 || x42 == x13 || x42 == x14 || x42 == x21 || x42 == x22 || x42 == x23 || x42 == x24 ||
x42 == x31 || x42 == x32 || x42 == x33 || x42 == x34 || x42 == x41)
continue;
if (x43 == x11 || x43 == x12 || x43 == x13 || x43 == x14 || x43 == x21 || x43 == x22 || x43 == x23 || x43 == x24 ||
x43 == x31 || x43 == x32 || x43 == x33 || x43 == x34 || x43 == x41 || x43 == x42)
continue;
if (x44 == x11 || x44 == x12 || x44 == x13 || x44 == x14 || x44 == x21 || x44 == x22 || x44 == x23 || x44 == x24 ||
x44 == x31 || x44 == x32 || x44 == x33 || x44 == x34 || x44 == x41 || x44 == x42 || x44 == x43)
continue;
int sh1 = x11 + x12 + x13 + x14, sh2 = x21 + x22 + x23 + x24, sh3 = x31 + x32 + x33 + x34, sh4 = x41 + x42 + x43 + x44;
int sv1 = x11 + x21 + x31 + x41, sv2 = x12 + x22 + x32 + x42, sv3 = x13 + x23 + x33 + x43, sv4 = x14 + x24 + x34 + x44;
int sd1 = x11 + x22 + x33 + x44, sd2 = x14 + x23 + x32 + x41;
if (sh1 != S || sh2 != S || sh3 != S || sh4 != S || sv1 != S || sv2 != S || sv3 != S || sv4 != S || sd1 != S || sd2 != S)
continue;
printf("%d %d %d %d %d %d %d %d %d %d %d %d %d %d %d %dn", x11, x12, x13, x14, x21, x22, x23, x24, x31, x32, x33, x34, x41, x42, x43, x44);
squares++;
}
}
}
}
}
}
}
}
}
printf("CNT: %dn", squares);
float diff_t = float(clock() - begin_time)/CLOCKS_PER_SEC;
printf("T = %.2fsn", diff_t);
return 0;
}
Это гораздо лучше — т.к. задача практически идеально распараллеливается (расчеты в каждой ветви не зависят друг от друга), время меньше примерно в число раз, равное количеству ядер процессора. Но увы, принципиально большего из этого кода не получить, хотя какими-то оптимизациями может и можно выиграть несколько процентов. Переходим к более тяжелой артиллерии, расчетам на GPU.
Вычисления с помощью NVIDIA CUDA
Если не вдаваться в подробности, то процесс вычислений, выполняющийся на видеокарте, можно представить как несколько параллельных аппаратных блоков (blocks), каждый из которых выполняет несколько процессов (threads).

Для примера можно привести пример функции сложения 2х векторов из документации CUDA:
__global__
void add(int n, float *x, float *y)
{
int index = threadIdx.x;
int stride = blockDim.x;
for (int i = index; i < n; i += stride)
y[i] = x[i] + y[i];
}Массивы x и y — общие для всех блоков, а сама функция таким образом выполняется одновременно сразу на нескольких процессорах. Ключ тут в параллелизме — процессоры видеокарты гораздо проще чем обычный CPU, зато их много и они ориентированы именно на обработку числовых данных.
Это то, что нам нужно. Мы имеем матрицу чисел X11, X12,..,X44. Запустим процесс из 16 блоков, каждый из которых будет выполнять 16 процессов. Номеру блока будет соответствовать число X11, номеру процесса число X12, а сам код будет вычислять все возможные квадраты с для выбранных X11 и X12. Все просто, но здесь есть одна тонкость — данные нужно не только вычислить, но и передать с видеокарты обратно, для этого в нулевом элементе массива будем хранить число найденных квадратов.
Основной код получается весьма простым:
#define N 4
#define SQ_MAX 8*1024
#define BLOCK_SIZE (SQ_MAX*N*N + 1)
int main(int argc,char *argv[])
{
const clock_t begin_time = clock();
int *results = (int*)malloc(BLOCK_SIZE*sizeof(int));
results[0] = 0;
int *gpu_out = NULL;
cudaMalloc(&gpu_out, BLOCK_SIZE*sizeof(int));
cudaMemcpy(gpu_out, results, BLOCK_SIZE*sizeof(int), cudaMemcpyHostToDevice);
squares<<<MAX, MAX>>>(gpu_out);
cudaMemcpy(results, gpu_out, BLOCK_SIZE*sizeof(int), cudaMemcpyDeviceToHost);
// Print results
int squares = results[0];
for(int p=0; p<SQ_MAX && p<squares; p++) {
int i = MAX*p + 1;
printf("[%d %d %d %d %d %d %d %d %d %d %d %d %d %d %d %d]n",
results[i], results[i+1], results[i+2], results[i+3],
results[i+4], results[i+5], results[i+6], results[i+7],
results[i+8], results[i+9], results[i+10], results[i+11],
results[i+12], results[i+13], results[i+14], results[i+15]);
}
printf ("CNT: %dn", squares);
float diff_t = float(clock() - begin_time)/CLOCKS_PER_SEC;
printf("T = %.2fsn", diff_t);
cudaFree(gpu_out);
free(results);
return 0;
}Мы выделяем блок памяти на видеокарте с помощью cudaMalloc, запускаем функцию squares, указав ей 2 параметра 16,16 (число блоков и число потоков), соответствующие перебираемым числам 1..16, затем копируем данные обратно через cudaMemcpy.
Сама функция squares по сути повторяет код из предыдущей части, с той разницей, что приращение количества найденных квадратов делается с помощью atomicAdd — это гарантирует что переменная будет корректно изменяться при одновременных обращениях.
// Compile:
// nvcc -o magic4_gpu.exe magic4_gpu.cu
#include <stdio.h>
#include <ctime>
#define N 4
#define MAX (N*N)
#define SQ_MAX 8*1024
#define BLOCK_SIZE (SQ_MAX*N*N + 1)
#define S 34
// Magic square:
// x11 x12 x13 x14
// x21 x22 x23 x24
// x31 x32 x33 x34
// x41 x42 x43 x44
__global__ void squares(int *res_array) {
int index1 = blockIdx.x, index2 = threadIdx.x;
if (index1 + 1 > MAX || index2 + 1 > MAX) return;
const int x11 = index1+1, x12 = index2+1;
for(int x13=1; x13<=MAX; x13++) {
if (x13 == x11 || x13 == x12)
continue;
int x14 = S - x11 - x12 - x13;
if (x14 < 1 || x14 > MAX) continue;
if (x14 == x11 || x14 == x12 || x14 == x13)
continue;
for(int x21=1; x21<=MAX; x21++) {
if (x21 == x11 || x21 == x12 || x21 == x13 || x21 == x14)
continue;
for(int x22=1; x22<=MAX; x22++) {
if (x22 == x11 || x22 == x12 || x22 == x13 || x22 == x14 || x22 == x21)
continue;
for(int x23=1; x23<=MAX; x23++) {
int x24 = S - x21 - x22 - x23;
if (x24 < 1 || x24 > MAX) continue;
if (x23 == x11 || x23 == x12 || x23 == x13 || x23 == x14 || x23 == x21 || x23 == x22)
continue;
if (x24 == x11 || x24 == x12 || x24 == x13 || x24 == x14 || x24 == x21 || x24 == x22 || x24 == x23)
continue;
for(int x31=1; x31<=MAX; x31++) {
if (x31 == x11 || x31 == x12 || x31 == x13 || x31 == x14 || x31 == x21 || x31 == x22 || x31 == x23 || x31 == x24)
continue;
for(int x32=1; x32<=MAX; x32++) {
if (x32 == x11 || x32 == x12 || x32 == x13 || x32 == x14 || x32 == x21 || x32 == x22 || x32 == x23 || x32 == x24 || x32 == x31)
continue;
for(int x33=1; x33<=MAX; x33++) {
int x34 = S - x31 - x32 - x33;
if (x34 < 1 || x34 > MAX) continue;
if (x33 == x11 || x33 == x12 || x33 == x13 || x33 == x14 || x33 == x21 || x33 == x22 || x33 == x23 || x33 == x24 || x33 == x31 || x33 == x32)
continue;
if (x34 == x11 || x34 == x12 || x34 == x13 || x34 == x14 || x34 == x21 || x34 == x22 || x34 == x23 || x34 == x24 || x34 == x31 || x34 == x32 || x34 == x33)
continue;
const int x41 = S - x11 - x21 - x31, x42 = S - x12 - x22 - x32, x43 = S - x13 - x23 - x33, x44 = S - x14 - x24 - x34;
if (x41 < 1 || x41 > MAX || x42 < 1 || x42 > MAX || x43 < 1 || x43 > MAX || x44 < 1 || x44 > MAX)
continue;
if (x41 == x11 || x41 == x12 || x41 == x13 || x41 == x14 || x41 == x21 || x41 == x22 || x41 == x23 || x41 == x24 ||
x41 == x31 || x41 == x32 || x41 == x33 || x41 == x34)
continue;
if (x42 == x11 || x42 == x12 || x42 == x13 || x42 == x14 || x42 == x21 || x42 == x22 || x42 == x23 || x42 == x24 ||
x42 == x31 || x42 == x32 || x42 == x33 || x42 == x34 || x42 == x41)
continue;
if (x43 == x11 || x43 == x12 || x43 == x13 || x43 == x14 || x43 == x21 || x43 == x22 || x43 == x23 || x43 == x24 ||
x43 == x31 || x43 == x32 || x43 == x33 || x43 == x34 || x43 == x41 || x43 == x42)
continue;
if (x44 == x11 || x44 == x12 || x44 == x13 || x44 == x14 || x44 == x21 || x44 == x22 || x44 == x23 || x44 == x24 ||
x44 == x31 || x44 == x32 || x44 == x33 || x44 == x34 || x44 == x41 || x44 == x42 || x44 == x43)
continue;
int sh1 = x11 + x12 + x13 + x14, sh2 = x21 + x22 + x23 + x24, sh3 = x31 + x32 + x33 + x34, sh4 = x41 + x42 + x43 + x44;
int sv1 = x11 + x21 + x31 + x41, sv2 = x12 + x22 + x32 + x42, sv3 = x13 + x23 + x33 + x43, sv4 = x14 + x24 + x34 + x44;
int sd1 = x11 + x22 + x33 + x44, sd2 = x14 + x23 + x32 + x41;
if (sh1 != S || sh2 != S || sh3 != S || sh4 != S || sv1 != S || sv2 != S || sv3 != S || sv4 != S || sd1 != S || sd2 != S)
continue;
// Square found: save in array (MAX numbers for each square)
int p = atomicAdd(res_array, 1);
if (p >= SQ_MAX) continue;
int i = MAX*p + 1;
res_array[i] = x11; res_array[i+1] = x12; res_array[i+2] = x13; res_array[i+3] = x14;
res_array[i+4] = x21; res_array[i+5] = x22; res_array[i+6] = x23; res_array[i+7] = x24;
res_array[i+8] = x31; res_array[i+9] = x32; res_array[i+10] = x33; res_array[i+11] = x34;
res_array[i+12]= x41; res_array[i+13]= x42; res_array[i+14] = x43; res_array[i+15] = x44;
// Warning: printf from kernel makes calculation 2-3x slower
// printf("%d %d %d %d %d %d %d %d %d %d %d %d %d %d %d %dn", x11, x12, x13, x14, x21, x22, x23, x24, x31, x32, x33, x34, x41, x42, x43, x44);
}
}
}
}
}
}
}
}
int main(int argc,char *argv[])
{
int *gpu_out = NULL;
cudaMalloc(&gpu_out, BLOCK_SIZE*sizeof(int));
const clock_t begin_time = clock();
int *results = (int*)malloc(BLOCK_SIZE*sizeof(int));
results[0] = 0;
cudaMemcpy(gpu_out, results, BLOCK_SIZE*sizeof(int), cudaMemcpyHostToDevice);
squares<<<MAX, MAX>>>(gpu_out);
cudaMemcpy(results, gpu_out, BLOCK_SIZE*sizeof(int), cudaMemcpyDeviceToHost);
// Print results
int squares = results[0];
for(int p=0; p<SQ_MAX && p<squares; p++) {
int i = MAX*p + 1;
printf("[%d %d %d %d %d %d %d %d %d %d %d %d %d %d %d %d]n", results[i], results[i+1], results[i+2], results[i+3],
results[i+4], results[i+5], results[i+6], results[i+7],
results[i+8], results[i+9], results[i+10], results[i+11],
results[i+12], results[i+13], results[i+14], results[i+15]);
}
printf ("CNT: %dn", squares);
float diff_t = float(clock() - begin_time)/CLOCKS_PER_SEC;
printf("T = %.2fsn", diff_t);
cudaFree(gpu_out);
free(results);
return 0;
}
Результат не требует комментариев — время выполнения составило 2.7с, что примерно в 30 раз лучше изначального однопоточного варианта:
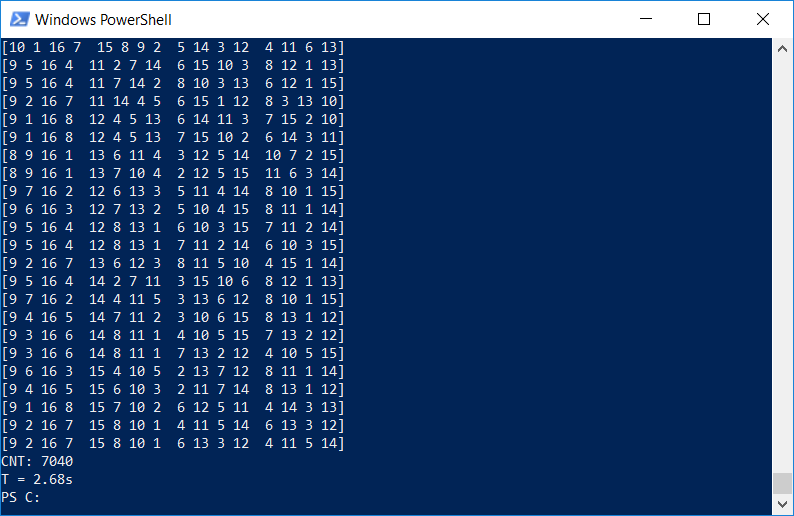
Скорее всего, это далеко не идеал, например можно запустить еще больше блоков на GPU, но это сделает код более запутанным и сложным для понимания. И разумеется, расчеты даются не «бесплатно» — при загруженном GPU интерфейс Windows начинает заметно подтормаживать, а энергопотребление компьютера увеличивается практически в 2 раза, с 65 до 130Вт.
Заключение
Задача нахождения «магических квадратов» оказалась технически весьма интересной, и в то же время непростой. Даже с вычислениями на GPU поиск всех квадратов 5х5 может занять несколько часов, а оптимизацию для поиска магических квадратов размерности 7х7 и выше, еще предстоит сделать.
Математически и алгоритмически, тоже есть несколько нерешенных моментов:
— Зависимость количества «магических квадратов» от N. Известно что квадрата 2х2 не существует, квадрат 3х3 существует всего 8, квадратов 4х4 как мы выяснили, 7040, но исключение поворотов или отражений в алгоритм пока не добавлено. Для больших размерностей вопрос пока открыт.
— Исключение квадратов, являющимися поворотами или отражениями уже найденного.
— Скорость и оптимизация алгоритма. К сожалению, потестировать код на суперкомпьютере или хотя бы на NVIDIA Tesla возможности нет, если кто-то может запустить, было бы интересно. Если у кого есть идеи по самому алгоритму, их тоже можно попробовать реализовать. При желании можно даже запустить распределенный проект по поиску квадратов, если конечно наберется достаточно число читаталей ;)
Об анализе и свойствах самих магических квадратов можно написать отдельную статью, если будет интерес.
PS: К вопросу, который наверняка последует, «а зачем это надо». С точки зрения расхода электроэнергии вычисление магических квадратов ничем не лучше или хуже вычисления биткоинов, так что почему бы и нет? К тому же, это интересная разминка для ума и интересная задача в области прикладного программирования.
Автор: DmitrySpb79