В нашем приложении есть фича, как у сына маминой подруги vivino — определение вина по фотографии. Под капотом — использование сторонних сервисов, Tineye — для определения наиболее подходящей этикетки, Google Vision — для чтения текста на ней. Последнее нужно для того, чтобы уточнить правильный продукт, т.к. поиск изображения не учитывает важность некоторых регионов, как правило — это текстовая информация — год и тип вина.
Однако, точность у обоих сервисов заметно снижается из-за того, что этикетка искажена цилиндрической поверхностью.
Особенно это заметно у Google Vision — любой текст за пределами центральной части этикетки практически не читается, хотя человек с легкостью его распознает. В этой статье я опишу, как обратить искажение и увеличить точность распознавания продуктов.

Прежде всего рассмотрим, что из себя представляет искажение.
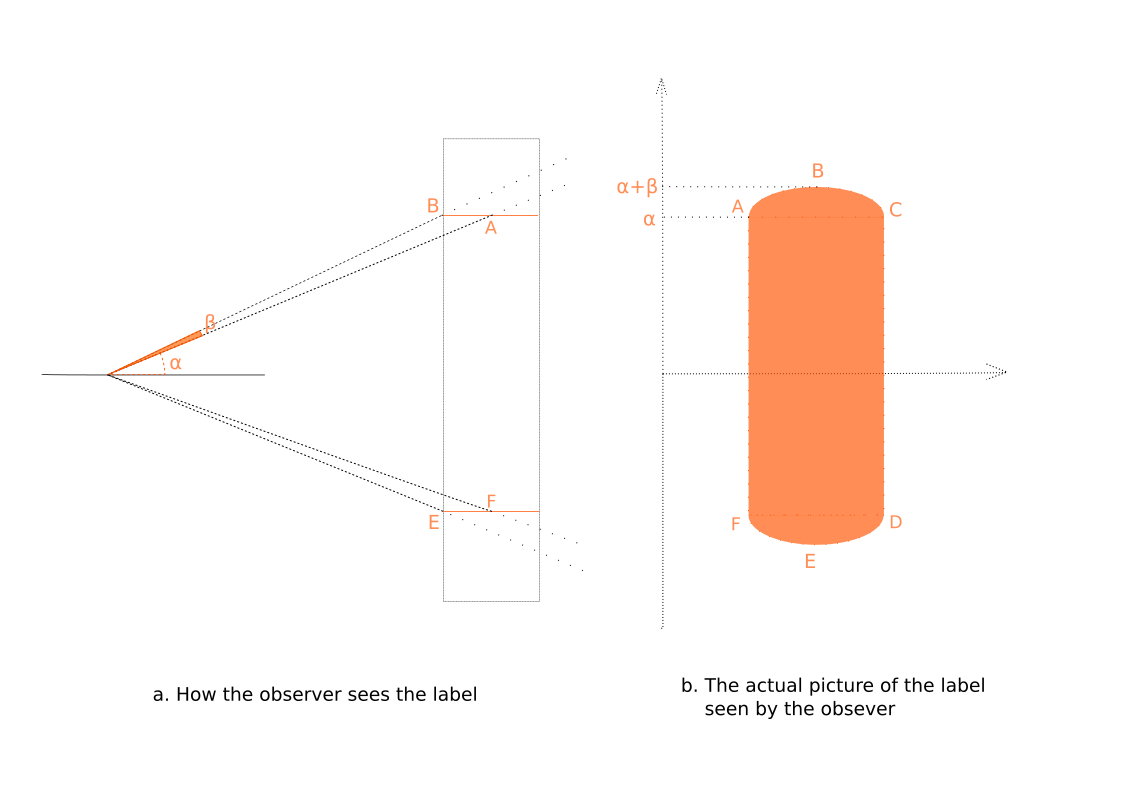
Прямоугольная этикетка, будучи наклеенной на цилиндр, имеет характерную форму бочки (b на схеме выше). Кривая ABC в данном случае, в довольно хорошем приближении, — эллипс, т.к. мы видим окружность (сечение цилиндра) под углом. Множество горизонтальных линий этикетки аналогично трансформируется во множество эллипсов на фотографии.
Самое интересное, что для разворачивания этикетки, достаточно указать 6 маркеров (ABCDEF):

И используя их, построить полную сетку поверхности:

Имея сетку поверхности, мы можем развернуть каждую плитку по отдельности, и получить исходную поверхность:

Код библиотеки доступен на гитхабе github.com/Nepherhotep/unwrap_labels
Удобство этого метода в то, что входные параметры для обратного преобразования — визуально определяемые характеристики этикетки (углы и верхняя, нижняя точки), что позволяет полностью автоматизировать процесс.
Следующая часть посвящена определению маркеров. Рабочий код доступен только частично в ветке github.com/Nepherhotep/unwrap_labels/tree/detect_ellipses, т.к. реально работающее решение покрыто хаками и шаманством, так что выкладывать в гитхаб такую жесть просто не позволяет совесть.
Этап первый — конвертируем изображение в черно-белый вариант.
Затем нужно получить контуры бутылки с этикеткой. Для этого мы используем трасформацию sobel en.wikipedia.org/wiki/Sobel_operator. Если вкратце, то этот фильтр сначала размывает изображение, а затем вычитает его из исходного. В итоге равномерные области остаются темными, а края (изменения) — светлыми.

Следующее, что нужно сделать — это определить две наиболее заметные вертикальные линии, которые, если повезет, являются краями бутылки. В данном случае это так и есть, но если фотографировать бутылку, стоящую рядом с другими бутылками, то это уже не так.
Чтобы определить эти линии, используем преобразование Хафа en.wikipedia.org/wiki/Hough_transform
Суть методики в том, что берем множество линий, идущих через весь экран, и считаем среднее значение пикселей (к примеру, берем линии, идущие с верхней части картинки в нижнюю часть). Эти значения переносим на новую координатную плоскость и получаем что-то вроде тепловой карты. На этой тепловой карте ищем два экстремума — они и есть боковые линии.
На схеме ниже видно, как левая линия переходит в точку на новой координатной плоскости:

С эллипсами чуть сложнее, но зная, что преобразование Хафа можно применять на любые математически заданные кривые, воспользуемся этим методом снова, но на этот раз будем искать множество кривых-эллипсов.
Но для начала нужно привести задачу к двумерному виду. Зная, что бутылка центрально симметричная, возьмем центральную ось за Y координату, а одну из сторон — за X. В качестве значений на новой координатной плоскости возьмем множество эллипсов, построенных между центральной осью и боковой стороной. Это возможно благодаря тому, что произвольная точка боковой стороны и центральной оси имеют только один способ соединения. Возможно, это не очень очевидно с первого взгляда, но куда проще для понимания, если обратиться к параметрической формуле эллипса:
x = a * cos(t)
y = b * sin(t)

Точно таким же образом найдем два искомых экстремума, которые определят два эллипса этикетки (кривые A-B, F-E). Теперь, когда у нас есть все необходимые параметры этикетки (боковые кривые, а также верхний и нижний эллипсы), мы можем применить алгоритм из первой части статьи и выполнить обратное преобразование.
Что можно улучшить. Во-первых, алгоритм не учитывает искажение перспективы самого эллипса, как следствие, боковые фрагменты этикетки растягиваются чуть сильнее, чем следует. Чтобы внести поправку, нужно знать реальный угол обзора камеры, либо, хотя бы, использовать наиболее типичный для телефона (можно подобрать эмпирически).
Во-вторых, преобразование Хафа довольно неустойчиво работает в сложных условиях — например, когда в кадр попадают рядом стоящие бутылки, и края интересующей бутылки могут определиться неправильно.
В третьих, если этикетка не прямоугольной формы (к примеру, эллиптической), то маркеры будут определены неправильно, и трансформация только сильнее исказит изображение.
На практике, куда интереснее использовать нейронную сеть для определения маркеров, т.к. ее можно тренировать, используя и сложные примеры, чтобы, как минимум, алгоритм не выполнял траснсформацию, если маркеры невозможно определить. Но пока я еще не пробовал применять нейронку для этой задачи, так что, возможно, это будет тема отдельной статьи :)
Автор: Nepherhotep

