OpenCV — популярная библиотека, включающая множество алгоритмов компьютерного зрения и функций для них. Оптимизация их под RISC-V — большая и интересная задача, которой в рамках Зимней школы RISC-V YADRO сезона 2024–2025 занимались студенты Университета Лобачевского (ННГУ). В этой статье они подробно расскажут о своей работе.

В проекте можно задействовать автоматическую векторизацию базовых функций компилятором. Или использовать универсальные интринсики — это метод векторизации, предоставляющий унифицированный интерфейс для общих инструкций. В итоге для работы выбрали RISC-V Vector Extension (RVV) — с этим расширением можно динамически управлять шириной секции SIMD, не полностью заполнять регистры и гибко управлять «хвостами».

Перейдем к оптимизации конкретных функций.
Flip
Функция flip — это отражение изображения по горизонтали или вертикали. Исходный код функции на C++ включает реверсирование байтов, а под RVV его прямого аналога не было. Поэтому мы скомпилировали другие инструкции:
inline int flipsu(const uchar * src, size_t sro_step, uchar * dst, size_t dst_step, int width, int height, int flip_code) {
if (flip_code == 0) 1// Vertical flip
for (int i = 0; i < height; ++i) {
const uchar * src_row = sro + i * src_step;
uchar * dst_row = dst + (height – 1 – i) * dst_step;
int j = 0;
while (j < width) {
size_t vl = __riscv_vsetvl_e8m1 (width – j);
vuint8m1_t v_src = __riscv_vle8_v_u8m1(src_row + j, vl);
__riscv_vse8_v_u8m1(dst_row + j, v_src, vl);
j += vl;
}
}
} else if (flip_code > 0) { // Horizontal flip
for (int i = 0; i < height; ++i) {
const uchar * src_row = src + i * src_step;
uchar * dst_row = dst + i * dst_step;
int j = 0;
while (j < width) {
size_t vl = __riscv_vsetvl_e0m1(width – j);
vuint8m1_t v_src = __riscv_vle8_v_u8m1(src_row + j, vl);
vuint8m1_t v_dst = __riscv_vrgather_vx_u8m1(v_src, vl – 1, vl);
for (size_t k = 1; k < vl; ++k) {
v_dst = __riscv_vrgather_vx_u8m1(v_dst, vl – 1 – k, vl);
}
__riscv_vse8_v_u8m1(dst_row + (width - j - vl), v_dst, vl);
j += vI;
}
}AddWeighted8u
Функция addWeighted8u — это взвешенное сложение двух матриц с последующей обрезкой диапазона значений до [0, 255] при работе с восьмибитными изображениями. В функцию передаются две картинки и коэффициенты, которые показывают вес каждой из картинок в результирующем изображении. Основная формула выглядит так:
dst = alpha*src1 + beta*src2 + gammaОсновная часть проекта — реализация референсного кода и приведение его в соответствие с тестами точности с помощью векторных инструкций RISC-V:
inline int addweighted8u(const uchar* src1, size_t step1,
const uchar* src2, size_t step2, uchar* dst, size_t step,
int width, int height, const void* _scalars) {
const float* scalars = static_cast<const float*>(_scalars);
int alpha = 1;
int beta = 1;
int gamma = 0;
int total_elements = width * height;
int j = 0;
while (j < total_elements) {
size_t vl =_riscv_vsetvl_e8m1(total_elements – j);
// Calculate the 1D index for src1, src2, and dst
const uint8_t* p_src1 = src1 + j;
const uint8_t* p_src2 = src2 + j;
uint8_t* p_dst = dst + j;
vuint8m1_t v_row1 = __riscv_vle8_v_u8m1(p_src1, vl);
vuint8m1_t v_row2 = __riscv_vle8_v_u8m1(p_src2, vl);
vuint16m2_t v_row1_w = __riscv_vwcvtu_x_x_v_u16m2(v_row1, vl);
vuint16m2_t v_row2_w = __riscv_vwcvtu_x_x_v_u16m2(v_row2, vl);
// Compute weighted sum
vuint16m2_t v_res = __riscv_vmul_vx_u16m2(v_row1_w, alpha, vl);
v_res = __riscv_vwmaccu_vx_u16m2(v_res, beta, v_row2, vl);
v_res = __riscv_vadd_vx_u16m2(v_res, gamma, vl);
// Clamp results to [0, 255]
v_res =__riscv_vmaxu_vx_u16m2(v_res, 0.0f, vl);
v_res =_riscv_vminu_vx_u16m2(v_res, 255.0f, vl);Скалярные операции мы заменили на векторные, чтобы обрабатывать несколько элементов. Для обработки типов использовали переход из uint8_t в uint16_t (расширение битности) с помощью инструкций vwcvtu. В процессе терялось много данных, поэтому попробовали реализацию с 32-битными float. Она не прошла тесты на точность, мы откатились обратно к референсному коду и попробовали инструкции без float. Здесь проблем с тестированием не возникло, но к дедлайну мы успели завершить только операции с int. В дальнейшем планируем доработку.
Split8u
Функция split8u разбивает многоканальное изображение на несколько одноканальных:
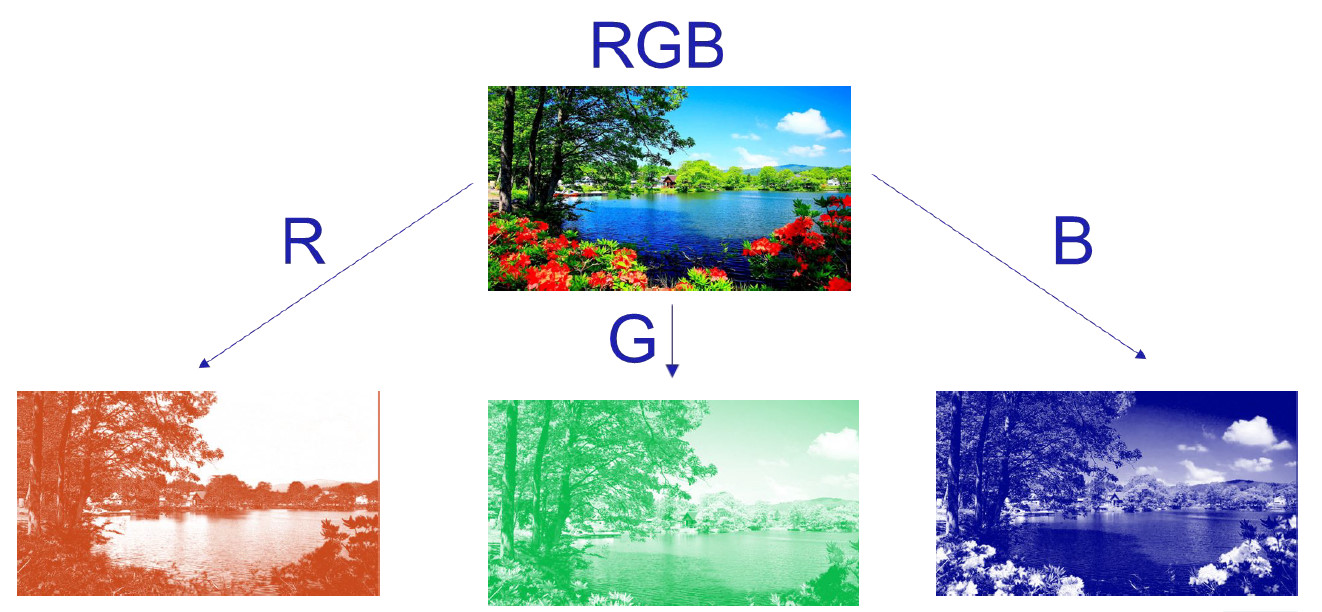
В ней есть массив src, где мы храним картинку, а также два массива dst для ее одноканальных составляющих. В процессе работы мы просто проходим по циклу и сохраняем в массиве dst значение src. Вот код после оптимизации:
vl = __riscv_vsetvlmax_e8m8();
i = 0;
uchar *dst0 = dst[0], *dst1 = dst[1];
for (; i <= len - vl * 4; i += vl * 4) {
auto a1 = __riscv_vlse8_v_u8m_1(src + i * cn, cn, vl);
auto b1 = __riscv_vlse8_v_u8m_1(src + 1 + i * cn, cn, vl);
…
auto a4 = __riscv_vlse8_v_u8m_1(src + (i + Vl + vl + vl) * cn, cn, vl);
auto b4 = __riscv_vise8_v_u8m_1(src + 1 + (i + vl + vl + vl) * cn, cn, vl);
__ riscv_vse8_v_ u8m1(dst0 + i, a1, vl);
__ riscv_vse8_v_ u8m1(dst1 + i, b1, vi);
...
__ riscv_vse8_v_u8m1(dst0 + i + vl + vl + vl, a4, vl);
__ riscv_vse8_v_u8m1(dst1 + i + vl + vl + vl, b4, vl);
}Мы взяли значение vl с помощью интринсика __riscv_vsetvlmax_e8m8() и произвели ручной loop-unrolling на четыре элемента, что ускорило работу функции. Но наибольшее увеличение производительности дало уменьшение размера маски интринсиков — сохранения и загрузки до единичного размера.

По сравнению с реализацией без интринсиков наша оказалась быстрее в 6–7, а иногда и в 12 раз. Разница с универсальными интринсиками тоже значительна: у нас быстрее в 2–3, а иногда и в 5 раз. Более подробно изучить функцию вы можете в pull request OpenCV.
InvSqrt32f
InvSqrt32f — это функция обратного квадратного корня. Она вызывается в void cv::pow(cv::InputArray src, -0.5, cv::OutputArray dst). Вот стандартная реализация:
void invSqrt32f(const float* src, float* dst, int len)Здесь используются универсальные интринсики, но они не заработали для нашей платформы — использовался обычный baseline-код. Вот наша реализация:
inline int invsqrt32f (const float *src, float *dst, const int len) {
const size_t vl = __riscv_vsetvl_e32m8(len);
const size_t remainings = len % vl;
auto cal_fun = [&](const size_t i, const size_t vl) {
printf("vl=%d,", vl);
vfloat32m8_t vsrc = __riscv_vle32_v_f32m8(&src[i], vl),
vres;
vres = __riscv_vfsqrt_v_f32m8(vsrc, vl);
vres = __riscv_vfrdiv_vf_f32m8(vres, 1., vl);
_riscv_vse32_V_f32m8(&dst[i], vres, vl);
};
size_t i = 0;
for (; i < len – remainings; i += vl)
calc_fun(i, vl);
if (remainings) {
size_t tail_len = __riscv_vsetvl_e32m8(len - i);
calc_fun(i, tail_len) ;
}
return CV_HAL_ERROR_OK;
}Она копирует восемь чисел float32 в буфер, вычисляет корень, делит единицу на корень и записывает обратно в память. С помощью vl вычисляются оставшиеся элементы. Для увеличения точности используется наивный алгоритм. В будущих стандартах RISC-V ISA, возможно, добавится поддержка интринсиков, которые будут вычислять значение обратного квадратного корня с точностью более семи знаков, что удовлетворит требованиям по высокой точности результата. Тогда получится заменить нашу оптимизацию одним интринсиком.
Sqrt32f
Sqrt32f — это приведение к квадратному корню 32-битной матрицы. После теста стандартной реализации мы оптимизировали ее через интринсики, выполняющие возведение под корень. Производительность в итоге улучшилась в 6–8,5 раз, причем разница увеличивалась по мере роста матриц:

Код нашей реализации:
inline int sqrt32f (const float *src, float *dst, int len) {
const size_t vl = __riscv_vsetvl_e32m8(len);
const size_t remainings = len % vl;
auto calc_fun = [&](const size_t i, const size_t vl) {
vfloat32m8_t vres;
{
vfloat32m8_t vsrc = __riscv_vle32_v_f32m8(&src[i], vl);
vres = __riscv_vfsqrt_v_f32m8(vsrc, vl);
}
_riscv_vse32_v_f32m8(&dst[i], vres, vl);
};
size t i = 0;
for (; i < len – remainings; i += vl)
calc_fun(i, vl);
if (remainings){
size_t tail_len = __riscv_vsetv1_e32m8(len - i);
calc_fun(i, tail_len);
}
return CV_HAL_ERROR_OK;
}Sqrt64f
В исходной библиотеке OpenCV функция sqrt64f реализована просто, через вызов в sqrt, который обрабатывает число типа double. Для оптимизации кода мы использовали векторные инструкции RVV: загрузку, сложение, деление, умножение и сохранение данных в векторных регистрах, а также метод Ньютона для итеративного вычисления.
void sqrt64f(const double* src, double* dst, int n) {
ssize_t i = 0;
ssize_t vlmax = __riscv_vsetvlmax_e64m1();
while(i < n) {
ssize_t vl = n - i;
if(vl > vlmax) vl = vlmax;
vl = __riscv_vsetvl_e64m1(vl);
vfloat64m1_t v_x = __riscv_vle64_v_f64m1(&src[i], vl);
vfloat64m1_t result = __riscv_vfmv_v_f_f64m1(static_cast<double>(0), vl);
vfloat64m1_t approx = __riscv_vfmv_v_f_f64m1(static_cast<double>(1), vl);
for(ssize_t step = 0; step < 100; ++step) {
approx = __riscv_vfadd_vv_f64m1(approx, __riscv_vfdiv_vv_f64m1(v_x, approx, vl), vl);
approx = __riscv_vfmul_vf_f64m1(approx, static_cast<double>(0.5), vl);
}
__riscv_vse64_v_f64m1(&dst[i], approx, vl);
i += vl;
}
}В итоге мы смогли достичь параллелизма, уменьшить накладные расходы цикла и повысить производительность.
Exp32f
Следующая функция для оптимизации — exp32f, экспонента одинарной точности. В стандартной реализации она вызывается через экспоненту, затем через функции декорации происходит выбор по типу данных. Мы переписали эту функцию через ряд Тейлора для аппроксимации экспоненты:
void exp32f( const float * x, float *y, int n )
{
CV INSTRUMENT REGION ();
const float* const expTab_f = cv::details::getExpTab32f(;
const float
A4 = (float) (1.000000000000002438532970795181890933776 / EXPPOLY_32F_A0),
A3 = (float) (.6931471805521448196800669615864773144641 / EXPPOLY_32F_A0),
A2 = (float) (.2402265109513301490103372422686535526573 / EXPPOLY_32F_A0),
A1 = (float) (.5550339366753125211915322047004666939128e-1 / EXPPOLY_32F A0);
int i = 0;
const Cv32suf* x = (const Cv32suf*)_x;
float minval = (float)(-exp_max_val/exp_prescale);
float maxval = (float)(exp_max_val/exp_prescale);
float postscale = (float)exp_postscale;
#if CV_SIMD
const int VECSZ = VTraits<v_float32>::vlanes();
const v_float32 vprescale = vx_setall_f32((float) exp_prescale) ;
const v_float32 vpostscale = vx_setall_f32((float) exp_postscale);
const v_float32 vminval = vx_setall_f32(minval);
const v_float32 vmaxval = vx_setall_f32(maxval) ;
const v_float32 vA1 = vx_setall_f32((float)A1);
const v_float32 vA2 = vx_setall_32((float) A2);
const v_float32 vA3 = vx_setall_f32((float)A3);
const v_float32 vA4 = vx_setall_f32((float)A4);
const v_int32 vidxmask = vx_setall_s32(EXPTAB_MASK) ;
bool y_aligned = (size_t)(void*)y % 32 == 0;Но по сравнению с оригинальной реализацией прогресса не получили:

По нашему мнению, в OpenCV экспонента уже реализована практически идеально. К тому же в своей реализации мы были ограничены по времени, и к коду явно могут возникнуть замечания. Можно поэкспериментировать с размером выходных регистров, динамически его менять, и тогда, возможно, мы придем к лучшим результатам.
Exp64f
Последней функцией в нашем проекте стала exp64f, которая принимает указатель на входной поток, указатель на выходной поток и размер самих потоков. Математическая основа нашей реализации — выражение экспоненты через степень числа 2, используя обычные свойства логарифмов. Далее мы конвертируем дробную часть в экспоненту обратно и раскладываем ее с хорошей точностью в ряд Тейлора, потому что она будет меньше единицы. Затем объединяем целую и дробную часть.
Вот основная функция нашей реализации — возведение 2 в степень целой части числа x (2int):
inline vfloat64m8_t pow2_v_i64m8_f64m8(vint64m8_t n, size_t vl)
{
const int64_t BIAS_64 = 1023;
vint64m8_t exp =_riscv_vadd_vx_i64m8(n, BIAS_64, vl);
vint64m8_t bits =_riscv_vs1l_vx_i64m8(exp, 52, vl);
return __riscv_vreinterpret_v_164m8_f64m8(bits);
}Здесь мы получаем показатели степеней, складываем их с весом, сдвигаем побитово и преобразуем биты в вещественное число с плавающей точкой. Теперь основной код:
vfloat64m8_t vx = __riscv_vle64_v_f64m8(sc + i, vl);
vx = __riscv_vfmul_vf_f64m8(vx, CL_M_LOG2E, vl);
vint64m8_t int_part = __riscv_vfcvt_x_f_v_i64m8(vx, vl);
vfloat64m8_t vpow2n = pow2_v_i64m8_f64m8(int_part, vl);
vfloat64m8_t frac_part = __riscv_vfsub_vv_f64m8(vx, __riscv_vfcvt_f_x_v_f64m8(int_part, vl), vl);
frac_part = _riscv_vfmul_vf_f64m8(frac_part, CV_LOG2, vl);
vfloat64m8_t term = frac_part;
vfloat64m8_t res = __riscv_vfadd_vf_f64m8(frac_part, 1.0, vl);
for (int j= 0; j < 10; ++j) {
term = __riscv_vfmul_vv_f64m8(term, frac_part, vl);
res = __riscv_vfmacc_vf_f64m8(res, factor_term[j], term, vl);
}
res = _riscv_vfmul_vv_f64m8(res, vpow2n, vl);
__riscv_vse64_v_f64m8(dst + i, res, vl);Первые две строчки — это выгрузка из входного потока аргументов. Дальше идет умножение их на логарифм, разделение на целую и дробную часть. Для целой части вызываем вспомогательную функцию возведения двойки, а с дробной частью используем полиномиальную аппроксимацию рядом Тейлора 12 порядка. В результате получается целая часть, умноженная на экспоненту дробной части.
Мы сравнили производительность нашей и оригинальной функции с помощью Banana Pi k1:

Мы выбрали LMUL M8, поскольку на M1, M2, M4 получалось ускорение в 4–6 раз, а на M8 — примерно в 8 раз. Если использовать матрицы, которые не делятся на 8, то в среднем мы получали ускорение от 7 до 7,5 раз. Для матриц, которые делятся на 8 — в 8, а иногда и в 9 раз.
Точность 10-13 мы подтвердили с помощью тестов OpenCV, а также с математической точки зрения: точность зависит только от разложения ряда Тейлора, то есть мы обеспечиваем точность до 12-го члена. Результаты нашей работы с этой функцией уже оформлены в pull request для OpenCV.
Состав команды ННГУ: Даниил Ануфриев, Владислав Лоскутов, Игорь Варфоломеев, Олеся Дудченко, Андрей Иванов, Дарья Карасева, Сергей Никоноров, Лев Прошлецов, Александр Лебедев, Евгений Кочнев.

Дмитрий Куртаев
куратор проекта, ведущий инженер по разработке ПО искусственного интеллекта YADRO
Оптимизируя функции OpenCV под RISC-V, студенты смогли посоревноваться не только против скалярного кода, но и с автоматической векторизацией с помощью универсальных интринсиков. Проект команды вышел за рамки Зимней школы. До финальной интеграции с доказанным улучшением производительности нам удалось довести методы split8u, invSqrt, exp и sqrt, merge.
Другие проекты Зимней школы RISC-V сезона 2024–2025:
Автор: yadro_team






