Недавно на arXiv.org была загружена статья с не очень интригующим названием "Neural reparameterization improves structural optimization" [arXiv:1909.04240]. Однако оказалось, что авторы, по сути, придумали и описали весьма нетривиальный метод использования нейросети для получения решения задачи структурной/топологической оптимизации физических моделей (хотя и сами авторы говорят, что метод более универсален). Подход очень любопытный, результативный и судя по всему, — совершенно новый (впрочем, за последнее не поручусь, но ни авторы работы, ни сообщество ODS, ни я, аналогов припомнить не смогли), поэтому его может быть полезно знать интересующимся как использованием нейросетей, так и решением разнообразных задач оптимизации.
О чём речь? Что за задача топологической оптимизации?
Вот представьте, что нужно, например, задизайнить какой-нить мост, многоэтажное здание, крыло самолёта, лопатку турбины или да не важно что. Обычно, это решается путём нахождения специалиста, например, архитектора, который бы с помощью своих знаний матана, сопромата, целевой области, а так же своего опыта, интуиции, тестовых макетов и т.д. и т.п. создавал бы нужный проект. Тут важно, что этот полученный проект был бы хорош только в меру хорошести этого специалиста. А этого, очевидно, не всегда достаточно. Поэтому когда компьютеры стали достаточно мощными, мы стали пытаться переложить подобные задачи на них. Ибо очевидно же, что компьютер может держать в памяти и обсчитывать... почему нет?
Такие задачи получили название "задачи структурной оптимизации", т.е. генерации оптимального дизайна несущих нагрузку механических структур [1]. Подразделом задач структурной оптимизации являются задачи топологической оптимизации (собственно, именно на них конкретно сфокусирована рассматриваемая работа, но это сейчас совершенно не суть и об этом потом). Типовая задача топологической оптимизации выглядит примерно так: для некого заданного концепта (мост, дом, и т.д.) в пространстве в двух или трёх измерениях, имея конкретные ограничения в виде материалов, технологий и иных требований, имея некоторые внешние нагрузки, нужно задизайнить оптимальную структуру, которая будет держать нагрузки и удовлетворять ограничениям.
- "Задизайнить" по сути означает найти/описать некоторое подпространство исходного пространства, которое надо заполнить строительным материалом.
- Оптимальность может быть выражена, например, в виде требования минимизации общего веса структуры при ограничениях в виде максимально допустимых стрессов в материале и возможных смещениях при заданных нагрузках.
Чтобы решить эту задачу на компьютере, целевое пространство решений дискретизируется в набор конечных элементов (пикселей для 2D и вокселей для 3D) и далее с помощью какого-то алгоритма компьютер решает, заполнить ли этот каждый индивидуальный элемент материалом или оставить его пустым?
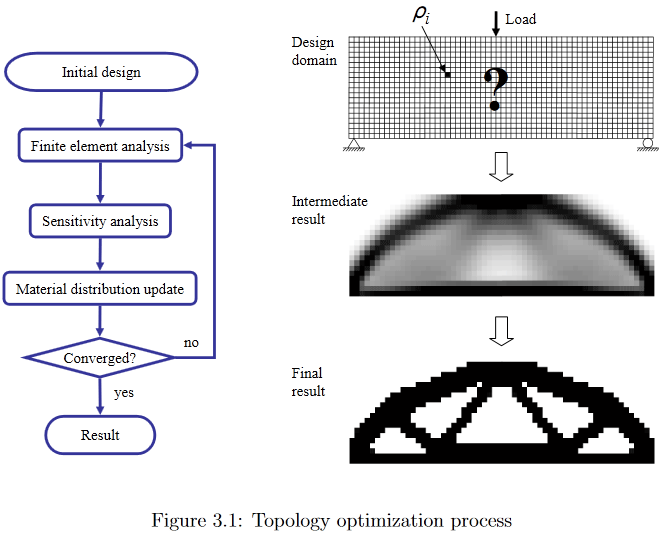
(Изображение из "Developments in Topology and Shape Optimization", Chau Hoai Le, 2010)
Так вот, уже из постановки задачи видно, что её решение — вполне себе крупная заноза для учёных. Желающим некоторых подробностей могу предложить, например, посмотреть весьма старый (2010 года, что всё же много для активно развивающейся области), зато достаточно подробный и легко гуглящийся диссер Chau Hoai Le с названием "Developments in Topology and Shape Optimization" [2], откуда я стащил верхнюю и нижнюю картинки.
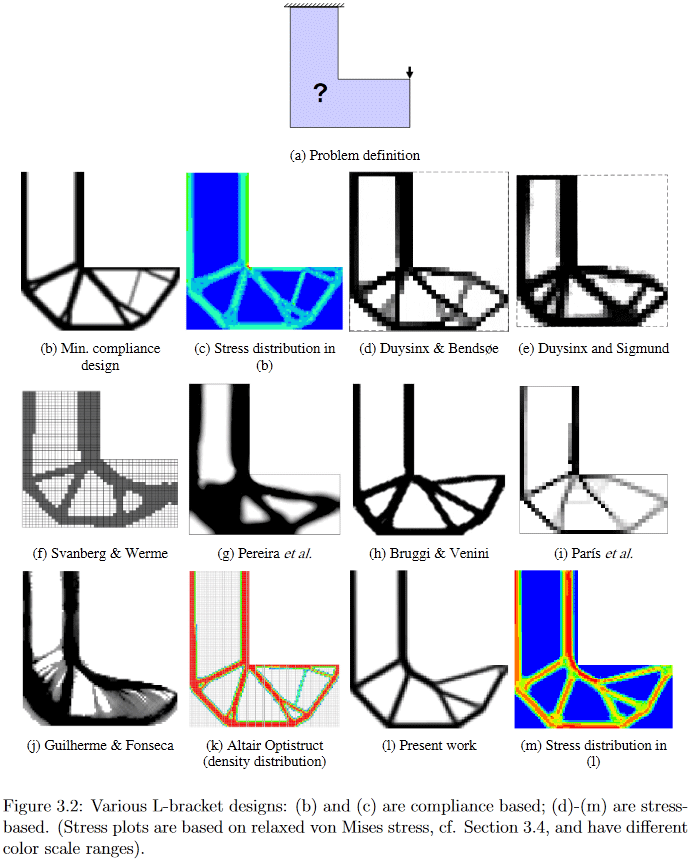
(Изображение из "Developments in Topology and Shape Optimization", Chau Hoai Le, 2010)
В качестве примера, на этой картинке хорошо видно, как очень по разному разными алгоритмами генерится решение вроде бы простой проблемы дизайна L-образного подвеса.
Так вот, теперь вернёмся к рассматриваемой работе.
Авторы весьма остроумно предложили решать такие задачи оптимизации с помощью дифференцируемой физической модели и хорошо известных в Машинном Обучении методов градиентного спуска, используя в качестве параметров модели веса и входы нейронной сети. По их словам (кода нет, и вообще нет ничего, кроме статьи и большого файла с примерами [4]), это даёт или такой же результат, как лучшие бейслайны на простых задачах, или лучшие бейслайнов на сложных.
Метод
Дальше я попробую описать, что и как конкретно авторы предложили делать, но сразу предупреждаю, что не гарантирую 100% правильности, ибо к моей уже несколько заржавевшей эрудиции в области ещё следует добавить кроме крайне скудной краткости описания ещё и некоторую общую "незрелость" статьи, находящейся, судя по наличию двух редакций за 4 дня, в процессе доработки.
Итак, их метод (применимый, как ненавязчиво напоминают авторы, к гораздо большему набору проблем оптимизации, чем только лишь одна структурная/топологическая оптимизация) глобально состоит из четырёх основных шагов.
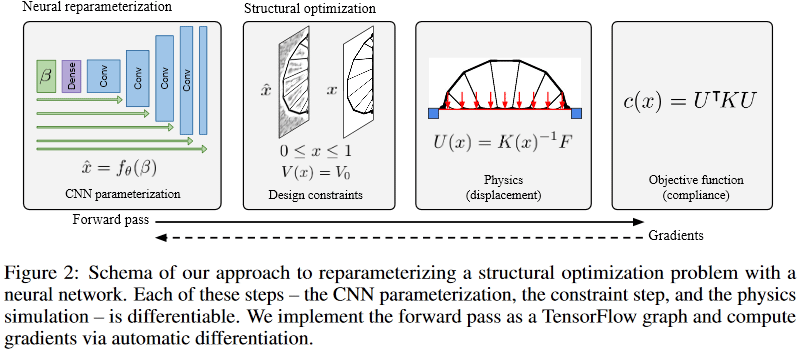
(Изображение из рассматриваемой публикации)
Шаг 1, генерация кандидата.
Нейросеть (далее НС) используя случайный первичный входной вектор _beta (он так же, как и веса сети, является тренируемым параметром), генерит (какую-то) картинку решения (работа идет с 2D, но на 3D, думаю, так же можно распространить). В качестве НС-генератора используется апсемплинговая часть известной архитектуры U-Net.
Шаг 2, применение ограничений и конвертация кандидата в каркас физ.модели.
Значения пикселей конвертируются в значения физических плотностей (насколько я понимаю из [2], они бинарны) в два шага. Сначала ненормализованные пикселы=логиты конвертятся в валидные значения плотности с помощью сигмоиды, помогающей выдерживать ограничение на общий объём использованного материала — для всей картинки подбирается бинарным поиском число-bias, которое вычитается из каждого пиксела и результат прогоняется через обычную сигмоиду (а bias выбирается так, чтобы общий объём полученных таким образом плотностей был бы равен некоторому наперёд заданному объёму V0); затем полученные значения плотности конвертятся в физическую плотность в пикселе с помощью некого cone-filter с радиусом 2 (Предположу, что речь идёт о каком-то фильтре из аппарата математической морфологии, возможно это он описан в главе 3.1 Density Filtering работы [3]).
Короче, суть в том, что на этом шаге ненормализованный выход вполне обычной НС превращается в правильно нормализованный каркас физической модели, к которому уже применены необходимые априорные ограничения (в работе это используемое количество материала).
Шаг 3, оценка полученного каркаса физической моделью.
Полученный каркас прогоняется через дифференцируемый физический движок, чтобы получить вектор(/тензор?) сдвига конструкции под нагрузкой (в т.ч. гравитацией) U. Ключевое здесь — дифференцируемость движка, что позволяет получать градиенты (напомню, что градиентом функции является в общем случае тензор, составленный из частных производных функции по всем её аргументам. Градиент показывает направление и скорость изменения функции в текущей точке, поэтому, зная его, можно "подкручивать" аргументы так, чтобы с функцией происходило нужное изменение — она уменьшалась или увеличивалась). Такой дифференцируемый физический движок не надо писать с нуля, — они давно существуют и хорошо известны. Авторам потребовалось лишь сделать их сопряжение с пакетами расчёта нейросетей, типа TensorFlow/PyTorch.
Шаг 4, вычисление значения целевой функции для каркаса/кандидата.
Рассчитывается подлежащая минимизации скалярная целевая функция с(x), описывающая податливость (она обратна жесткости) полученного каркаса. Функция податливости зависит от полученного на прошлом шаге вектора сдвига U и матрицы жесткости конструкции К (мне не хватает знаний по topology optimization, чтобы понять, откуда берётся К, — предположу, что, похоже, она напрямую считается из каркаса).
И далее — готово. Поскольку всё создаётся в среде с автоматическим дифференцированием, то на этом этапе мы автоматически получаем все градиенты целевой функции, которые проталкиваются благодаря дифференцируемости всех преобразований по каждому шагу обратно вплоть до весов и входного вектора генерирующей нейросети. Веса и вх.вектор соответственно своим частным производным изменяются, вызывая необходимое изменение — минимизацию целевой функции. Далее происходит новый цикл прямого прохода по НС -> применение ограничений -> просчёт физ.модели -> расчёт целевой функции -> новые градиенты и обновление весов. И так до схождения алго.
Важный момент, описания которого я не нашёл в работе, — как выбирается общий объём конструкции V0, с помощью которого выполняется конвертация кандидатного решения в каркас на шаге 2. От его выбора, очевидно, чрезвычайно зависят свойства получаемого решения. По косвенным признакам (все примеры полученных решений [4] имеют по несколько экземпляров, отличающихся как раз по ограничению объёма), предположу, что они просто фиксируют V0 на некой сетке из диапазона [0.05, 0.5] и затем сами глазками смотрят получаемые решения с разными V0. Ну, для концептуальной работы этого, в общем, и так достаточно, хотя, конечно, было б ужасно интересно посмотреть вариант с подбором так же и этого V0, но, это пойдёт, видимо, на следующий этап развития работы.
Второй важный момент, которого я так и не понял, это как они накладывают ограничения/требования на конкретный вид нужного решения. Т.е. если отделить мост от здания ещё можно благодаря физической модели (здание имеет полную опору, а мост — только в граничных концах), то как отделить, допустим, здание в 3 этажа от здания в 4 этажа?
Третьим непонятным лично мне моментом является вопрос устройства и дифференцируемости того самого cone-filter, с помощью которого на втором шаге нормализованные плотности превращаются в физические плотности (которые вроде бы бинарны?), используемые физической моделью. Впрочем, судя по всему, оба эти последние непонятные момента являются вполне стандартными в топологической оптимизации, поэтому авторы и не заостряли на них внимания.
Как это работает?
Оказалось, что для маленьких (в терминах размера пространства решения = количества пикселей) проблем, метод даёт ± аналогичное качество результатов, как и лучшие традиционные методы топологической оптимизации, но на больших (размер сетки от 2^15 и более пикселей, т.е., напр, от 128*256 и более) получение качественных решений методом более вероятно, чем лучшим традиционным (из 116 тестированных задач метод дал предпочтительное решение в 99 задачах, против 66 предпочтительных у лучшего традиционного).
Более того, вот тут начинается кое-что особенно интересное. Традиционные методы топологической оптимизации в больших задачах страдают от того, что на ранних этапах работы быстро формируют мелкомасштабную паутину, которая потом мешает развитию крупномасштабных структур. Это приводит к тому, что полученный результат бывает трудно/невозможно воплотить физически в жизнь. Поэтому вынужденно существует целое направление в задачах оптимизации топологии, которое изучает/придумывает методы, как же сделать получаемые решения более технологически удобными.
Здесь же, судя по всему, благодаря свёрточной сети, оптимизация происходит одновременно на нескольких пространственных масштабах одновременно, что позволяет избежать/сильно уменьшить "паутину" и получать более простые, но качественные и технологически-friendly решения!
Кроме того, опять же благодаря свёрточности сети, получаются вообще принципиально иные, чем в стандартных-традиционных методах, решения.
Например, в дизайнах:
- консольной балки (cantilever beam) метод нашёл решение всего из 8 составных частей, в то время как лучший традиционный — 18.
- моста с тонкими опорами (thin support bridge) метод выбрал одну опору с древоподобным паттерном ветвления, а традиционный — две опоры
- крыши (roof) метод использует колонны, а традиционный — ветвящийся паттерн. И т.д.
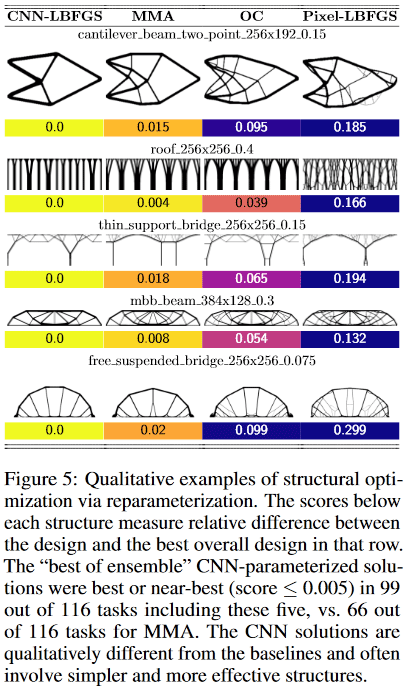
(Изображение из рассматриваемой публикации)
Что в целом в этой работе особенного?
Я никогда не видел такого использования нейросети. Обычно нейросети используют для получения некоторой очень хитрой и сложной функции y=F(x, theta) (где х — аргумент, а theta — настраиваемые параметры), которая умеет делать что-нибудь полезное. Например, если х — картинка с камеры автомобиля, то значением y функции может быть, например, признак есть ли в опасной близости к машине пешеход. Т.е. тут важно, что ценным является сам конкретный вид функции, которая многократно используется для решения какой-то задачи.
Здесь же — нейросеть используется как хитрое хранилище-модификатор-настройщик параметров некоторой физической модели, которое в силу самой своей архитектуры накладывает определённые ограничения на значения и вариации изменений этих параметров (собственно, примеры под заголовком Pixel-LBFGS представляют собой попытку оптимизировать пиксели напрямую, не используя нейросеть для их генерации, — результаты видны, НС важна). Вот тут-то становится критически важным свёрточность использованной нейросети, потому что именно её архитектура позволяет "поймать" концепт инвариантности переноса и немного поворота (представьте, что вы распознаёте текст с картинки — вам важно извлечь именно текст и при этом совершенно не важно, в какой части картинки он расположен и как повёрнут, — т.е. вам нужны инвариантность по переносу и повороту). В данной же задаче, какая-нибудь физическая палка, являющейся единицей строения и множество которых мы оптимизируем, всё так же остаётся ею независимо от положения и ориентации в пространстве.
Классическая полносвязная сеть, к примеру, тут бы, скорее всего, не сработала (так же хорошо), потому что её архитектура позволяет слишком многое/малое (ну вот да, такой дуализм, как посмотреть). В то же время, несмотря на то, что НС остаётся тут всё той же очень хитрой и сложной функцией y=F(x, theta), в этой задаче нам в конечном счёте вообще наплевать и на её аргумент х, и на её параметры theta, и на то, как будет использоваться функция. Нас волнует только лишь одное единственное её значение y, которое получается в процессе оптимизации одной конкретной целевой функции для одной конкретной физической модели, в которой {x, theta} — всего лишь настраиваемые параметры!
Вот это, по моему, афигенно крутая и новая идея! (хотя, конечно, потом, как всегда, может оказаться, что Шмидхубер описал её ещё в начале 90х, но поживём — увидим)
Вообще, по смыслу метод несколько напоминает обучение с подкреплением — там НС используется, грубо говоря, как "хранилище опыта" действующего в некоторой среде агента, которое обновляется по мере получения обратной связи среды на действия агента. Только там это самое "хранилище опыта" используется постоянно для принятия агентом новых решений, а тут — это всего лишь хранилище параметров физ.модели, от чего нам интересен лишь один единственный итоговый результат оптимизации.
Ну и последнее. Интересный момент бросился в глаза.
Вот так выглядят оптимальные решения для задачи многоэтажного здания:
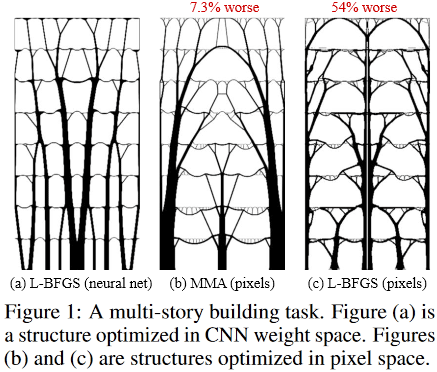
(Изображение из рассматриваемой публикации)
А вот так:

устроена внутри фантастическая Sagrada Familia, — Собор Святого Семейства, расположенный в Барселоне, Испания, который «дизайнил» гениальный Антонио Гауди.
[1]вариант определения задачи структурной/топологической оптимизации https://www.math.kth.se/optsyst/Struc.html
[2]"Developments in Topology and Shape Optimization" http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.174.4622&rep=rep1&type=pdf
[3]Morphology-based black and white filters for topology optimization, https://orbit.dtu.dk/files/3113841/preprint.pdf
[4]примеры решений https://arxiv.org/src/1909.04240v2/anc/all-designs.pdf
Автор: Алексей






