Variational Inference — что это такое и с чем это едят?

Привет!

Недавно пообщался с коллегами о вариационном автоэнкодере и выяснилось что многие даже работающие в Deep Learning знают о вариационном выводе (Variational Inference) и в частности Нижней вариационной границе только по наслышке и не до конца понимают что это такое.
В этой статье я хочу подробно разобрать эти вопросы. Кому интересено, прошу под кат — будет очень интересно.

Что такое вариационный вывод?

Семейство вариационных методов машинного обучения получили свое название от раздела математического анализа «Вариационного исчисления». В этом разделе изучаются задачи поиска экстремумов функционалов (функционал это функция от функций — т.е мы ищем не значения переменных в которых функция достигает своего максимума (минимума), а такую функцию при которой функционал достигает максимума (минимума).

Но возникает вопрос — в машинном обучении мы всегда ищем точку в пространстве параметров (переменных) в которых функция потерь имеет минимальное значение. Т.е это задача классического математического анализа, причем здесь Вариационное исчисление? Вариационное исчисление появляется в момент когда мы преобразуем функцию потерь в другую функцию потерь (зачастую это нижняя вариационная граница) используя методы вариацонного исчисления.

Зачем же нам это нужно? Разве нельзя напрямую оптимизировать функцию потерь? Эти методы нам необходимы когда напрямую получить несмещенную оценку градиента невозможно (либо эта оценка обладает очень высокой дисперсией). Например наша модель задает и , а нам необходимо вычислить . Это как раз, то для чего разрабатывался вариационный автоэнкодер.

Что такое Нижняя вариационная граница (Variational Lower Bound)?

Представим, что у нас есть функция . Нижняя граница на эту функцию будет любая функция , удовлетворяющая уравнению:

Т.е у любой функции существует бесчетное множество нижних границ. Все ли эти нижние границы одинаковы? Конечно нет. Введем еще одно понятие — невязка (я не нашел устоявшегося термина в русскоязычной литературе, в англоязычных статьях эту величину называют tightness):

Достаточно очевидно, что невязка всегда положительна. Чем меньше невязка — тем лучше.

Вот пример нижней границы с нулевой невязкой:

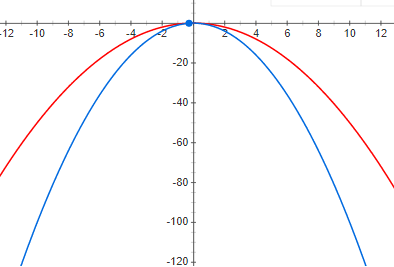
А вот пример с небольшой, но положительной невязкой:

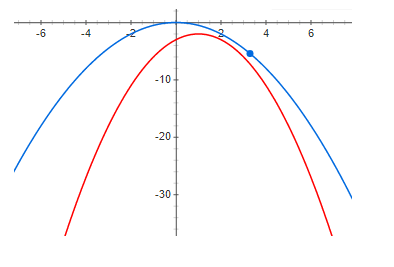
И наконец, достаточно большая невязка:

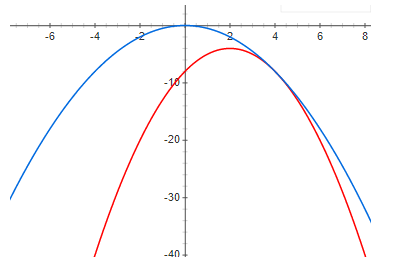
Из приведенных выше графиков отчетливо видно что при нулевой невязке максимум функции и максимум нижней границы находятся в одной точке. Т.е если мы хотим найти максимум некоторой функции, мы можем искать максимум нижней границы. В случае если невязка не нулевая, то это не так. И максимум нижней границы может быть очень далеко (по оси х) от искомого максимума. Из графиков видно что чем больше невязка, тем дальше максимумы могут быть друг от друга. В общем случае это неверно, но в большинстве практических случаев эта интуиция работает очень хорошо.

Вариационный автоэнкодер

Сейчас мы разберем пример очень хорошей нижней вариационной границы с потенциально нулевой невязкой (ниже будет понятно почему) — это Вариационный автоэнкодер (Variational Autoencoder).

Наша задача построить генеративную модель и обучить ее методом максимального правдоподобия. Модель будет иметь следующий вид:

где — плотность вероятности генерируемых семплов, — латентные переменные, — плотность вероятности латентной переменной (зачастую некая простая — например многомерное гауссовское распределение с нулевым матожиданием и единичной дисперсией — в общем что-то из чего мы можем легко семплировать), — условная плотность семплов при заданном значении латентных переменных, в вариационном автоэнкодере выбирается гауссовское с мат ожиданием и дисперсией зависящими от z.

Зачем нам может понадобиться представлять плотность данных в таком сложном виде? Ответ прост — данные имеют очень сложную функцию плотности и мы просто технически не можем построить модель такой плотности напрямую. Мы надеемся что эту сложную плотность можно хорошо аппроксимировать с помощью двух более простых плотностей и .

Мы хотим максимизировать следующую функцию:

где — плотность вероятности данных. Основная проблема в том, что плотность (при достаточно гибких моделях) не удается представить аналитически, а соответственно обучать модель.

Используем формулу Байеса и перепишем нашу функцию в следующем виде:

К сожалению, все также сложно посчитать (невозможно взять интеграл аналитически). Но во-первых заметим что выражение под логарифмом не зависит от z, значит можно взять математическое ожидание от логарифма по z от любого распределения и это не изменит значения функции и под знаком логарифма умножить и поделить на это же распределение (формально мы имеем лишь одно условие — данное распределение нигде не должно обращаться в нуль). В итоге мы получим:

заметим что во-первых второе слагаемое — KL дивергенция (а значит всегда положительна):

и во-вторых не зависит ни от ни от . Отсюда следует что,

где — нижняя вариационная граница (Variational Lower Bound) и достигает своего максимума когда — т.е распределения совпадают.

Положительность и равенство нулю тогда и только тогда когда распределения совпадают KL-дивергенции доказываются именно вариационными методами — отсюда и название вариационная граница.

Хочу заметить, что использование вариационной нижней границы дает несколько преимуществ. Во-первых дает нам возможность оптимизировать функцию потерь градиентными методами (попробуйте сделать это когда интеграл аналитически не берется) и во-вторых приближает обратное распределение распределением — т.е мы можем не только семплировать данные, но и семплировать латентные переменны. К сожалению, главный недостаток — при недостаточно гибкой модели обратного распределения, т.е когда семейство не содержит — невязка будет положительной и равной:

а это означает что максимум нижней границы и функции потерь скорее всего не совпадают. Кстати, вариационный автоэнкодер примененный для генерации картинок генерирует слишком смазанные изображения, думаю это как раз из-за выбора слишком бедного семейства .

Пример не очень хорошей нижней границы

Сейчас мы рассмотрим пример, где с одной стороны нижняя граница обладает всеми хорошими свойствами (при достаточно гибкой модели невязка будет нулевой), но в свою очередь не дает никакого преимущества перед использованием оригинальной функции потерь. Я считаю, что этот пример является очень показательным и если не делать теоретический анализ можно потратить очень много времени пытаясь обучать модели которые не имеют никакого смысла. Вернее модели имеют смысл, но если мы можем обучить такую модель, то уже проще выбирать из этого же семейства и использовать принцип максимального правдоподобия напрямую.

Итак, мы будем рассматривать точно такую же генеративную модель как и в случае вариационного автоэнкодера:

обучать будем все тем же методом максимального правдоподобия:

Мы все так же надеемся, что будет намного «проще» чем .
Только теперь распишем немного по-другому:

используя формулу Дженсена (Jensen) получим:

Вот именно в этом моменте большинство людей отвечают не задумавшись, что это действительно нижняя граница и можно обучать модель. Это действительно так, но давайте посмотрим на невязку:

откуда (применив формулу Ьайеса два раза):

легко заметить, что:

Давайте посмотрим что будет если мы будем увеличивать нижнюю границу — невязка будет уменьшаться. При достаточно гибкой модели:

казалось бы все отлично — нижняя граница обладает потенциально нулевой невязкой и при достаточно гибкой модели все должно работать. Да это действительно так, только внимательные читатели могут заметить что нулевая невязка достигается когда и являются независимыми случайными величинами!!! и для хорошего результата «сложность» распределения должна быть ничуть не меньше чем . Т.е нижняя граница не дает нам никаких преимуществ.

Выводы

Нижняя вариационная граница — отличный математический инструмент, позволяющий приближенно оптимизировать «неудобные» для обучения функции. Но как и любой другой инструмент нужно очень хорошо понимать его преимущества и недостатки а также использовать очень аккуратно. Мы рассмотрели очень хороший пример — вариационный автоэнкодер, а также пример не очень хорошей нижней границы, при этом проблемы этой нижней границы сложно увидеть без детального математического анализа.

Надеюсь это было хоть немного полезно и интересно.

Автор: Yurec666

Источник