
Пятница. Поэтому сегодня — пост позитива.
Настоящие программисты пишут программы не потому, что за них платят, а потому, что это им нравится. Решить задачу, которая кажется совершенно неразрешимой, — инсайт, озарение, прозрение – все это дает незабываемое ощущение восторга и пополняет копилку счастливых моментов жизни.
Поэтому предлагаю сегодня хабрсообществу поделиться своими историями успеха.
Начну с себя.
Было это 100500 лет назад, когда правильные программисты не писали в программе Х / 3, а только Х * 0.333333333333. Тогда мы разрабатывали сложные имитационные модели космических систем. Над комплексом имитационного моделирования работали примерно 300 человек. Наукоемкие модели. Сложные алгоритмы. Аэродинамика, упругость, прочность, двигатели, гироскопы, плазма в атмосфере и много чего еще. И десятки тысяч взаимодействующих объектов. Настоящий кайф!
В задачу моей команды входило комплексирование, интеграционное тестирование, проведение и анализ результатов имитационных экспериментов. Далее три коротких истории успеха о том, как удалось решить проблемы, которые на первый взгляд, казались непреодолимыми.
История первая. Учите матчасть!

Принесли компонент, который должен был моделировать активный участок полета ракеты-носителя (РН). Подключили к модулю-модели движения. Задали параметры. Запустили тест. Компонент отработал успешно. Проверили результат (начальные условия для компонента моделирующего орбитальный полет). Все правильно. Полетели дальше. Программа модели движения обрушилась. Хотя раньше уже была протестирована именно на этих начальных условиях. Не-по-нят-но…
Поменяли параметры модели активного участка. Все повторилось. Однако модель орбитального полета упала совершенно в другом месте и с другой ошибкой. Совсем не-по-нят-но…
Открыли исходники модели активного участка. Сразу бросилось в глаза объявление вектора, описывающего состояние РН (положение, скорость). Размер, вместо положенных 6, заявлен 9. Странненько…
— А нафига 9 ячеек в массиве?
— А это защита от ошибок. Если я запишу в лишнюю ячейку, то моя программа не свалится из-за выхода за границы массива.
— [мысленно] Ну-ну… И где тебя, @#$%^, только учили?
Пересобрали модуль в режиме отладки. Полетели, не спеша, в дебагере. Дошли до места падения. Упс… Входной параметр процедуры N равен 2, хотя на первом шаге алгоритма всегда должен быть равен 1. Нашли место в коде, где он инициализируется. Читаем N = 1. Что за ^%$#@ ?! Ни-че-го не понимаю!
— Что это?
— Вызов метода Рунге-Кутты.
— А почему первый параметр литерал?
— Потому что, мне наужен только один шаг интегрирования.
— Так он же, @#$%^, перевычислямый!!!
Учите матчасть!
«В фортране параметры передаются только по ссылке (указателю). Поэтому следует быть особо аккуратным при программировании передачи входного параметра. Входной параметр не должен перевычисляться в подпрограмме. Иначе при подстановке константы в качестве значения входного параметра по возвращении из подпрограммы константа будет испорчена» (с) Учебное пособие.
История вторая. Даже кодирование готового алгоритма есть процесс творческий
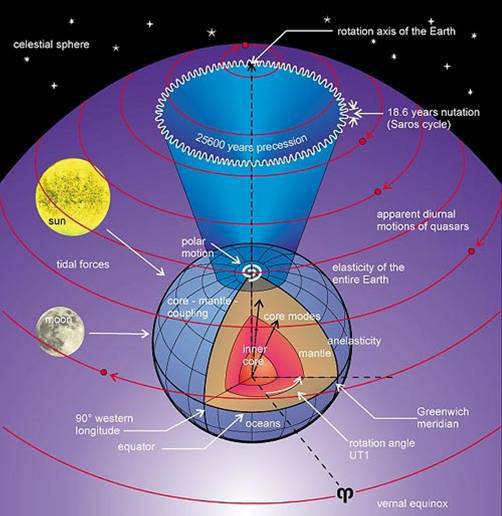
Для долгосрочных прогнозов траекторий КА потребовалась более точная модель вращения Земли.
Некоторые думают, что Земля равномерно вращается вокруг неподвижной оси со скоростью 1 оборот за 24 часа. Однако, это не так. Земная ось под влиянием притяжения Солнца, Луны и планет совершает в пространстве прецессионное движение и нутационные колебания.
В «Астрономическом ежегоднике РАН» регулярно публикуются многолетние данные натурных измерений вращения Земли. Там же публикуется алгоритм построения модели, экстраполирующей это движение. Модель представляет собой разложение угловой скорости по достаточно сложной системе функций. Разложение содержит около сотни членов. Коэффициенты этого разложения подобраны каким-нибудь методом наименьших квадратов по эмпирическим данным. Заявленная точность аппроксимации, если не изменяет память, составляет 10 ^ -10. Там же приводятся результаты расчетов, сделанные по этой модели.
С точки зрения программирования, эта задача, на первый взгляд, является тривиальной. Однако, этот случай запомнился мне по двум причинам.
Первая. При разработке этой программы я поставил абсолютный личный рекорд производительности: 2000 SLOC (отлаженных и оттестированных) за рабочий день (правда, рабочий день продолжался часов 14-16).
Вторая. Я навсегда утвердился в том, что даже простое кодирование готового алгоритма есть процесс творческий. И вот почему.
Я собрал в кулак всю свою волю и сконцентрировал все свое внимание, поскольку помимо того, что мне требовалось запрограммировать достаточно сложную систему функций, необходимо было еще безошибочно ввести достаточно много констант, которые содержали по 12 десятичных разрядов (работали без сканеров, не было их тогда). На это у меня ушли первые 8 рабочих часов.
Наконец, собрав программу целиком, я достаточно быстро выявил и устранил явные ошибки, которые являлись причиной того, что полученные результаты отличались от искомых в разы.
И тут случилась катастрофа. Результаты расчета по моей программе стали почти правильными. Это «почти» заключалось в двух последних десятичных знаках, т.е. относительная ошибка расчета имела величину 10 ^ -8, но абсолютная-то точность отличалась в 100 раз!
Каждый программист знает, как сложно искать ошибку в почти правильной программе. Остальные часы я потратил на безуспешные попытки выявить источник ошибок, в основном вычитывая код и проверяя коэффициенты.
Пришлось со своими проблемами пойти к Гуру.
– Ты знаешь, что разрядная сетка представления десятичного числа на компьютере конечна?
— [мысленно] А я что, типа не в курсе?
— А члены разложения по абсолютному значению отличаются на сотни порядков
— [мысленно] Да знаю я все!,
— Поэтому складывать их надо, начиная с самых маленьких.
— [мысленно] Упс…, а нас этому не учили.
Верю, что сейчас уже учат.
После внесения необходимых исправлений я, наконец-то, получил искомый результат.
Спасибо всем у кого мы учились…
История третья. «Мы получили очень похожий результат, но…»
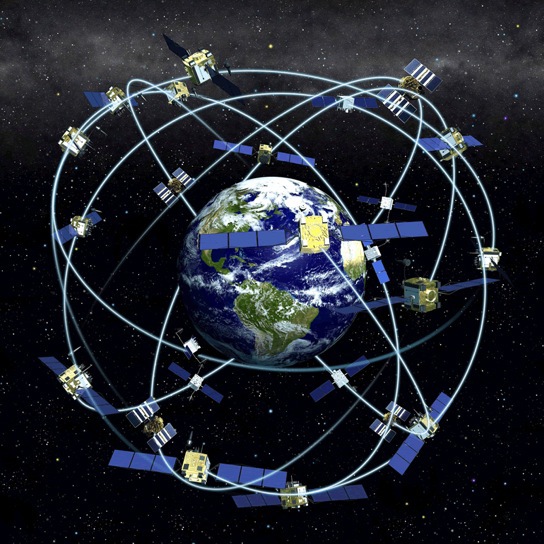
Для построения оптимальной орбитальной структуры регионально европейской спутниковой навигационной системы (Проект ПРОПНАСС. Следов в Интернете почти не осталось. Нашел одну страничку здесь, стр. 29. На фотографии я тоже есть :) ) требовалось уметь определять на достаточно длительном промежутке времени статистические характеристики навигационного поля. В первом приближении задача сводилась к вычислению как функции времени доли площади земной поверхности, из которой одновременно можно наблюдать 4 спутника из группировки.
Причем, наш практичный немецкий заказчик устроил соревнование и поручил эту же задачу параллельно решать коллегам из Брауншвейгского Технического университета.
Очевидно, что сначала мы попытались пойти простейшим путем и решить задачу методом прямого перебора на компьютере, разбив поверхность Земли на географическую сетку. Более рациональные методы оптимизации не подошли, поскольку критерий, по которому проводилась оптимизация, представлял из себя довольно «рваную» функцию.
Однако, быстро пришлось признать бесперспективность прямого перебора. Для решения этой задачи у нас был всего один Intel 486 и расчет значения критерия оптимальности на одном узле сетки занимал 15 минут. Посчитали. Получилось, что мы ни только не получим решение к обещанному сроку, но и не дождемся его в течение года непрерывных расчетов.
Требовалось повысить быстродействие алгоритма вычисления площади кратного покрытия зонами видимости навигационных КА, не менее чем в 100 раз, что было не реально. Нужно был искать другой подход.
С этой задачей я промучился недели три, периодически, то отбрасывая ее (вытисняя в подсознание), то снова возвращаясь к ней.
И, наконец! Инсайт, озарение, прозрение — восторг!
Решение пришло во сне. Причем в предыдущий вечер я этой задачей не занимался. Естественно я проснулся от неожиданности и часа 2 потратил на запись сна в виде математических формул. Придя на работу, я за несколько часов запрограммировал и отладил изобретенный алгоритм. Всего 100-150 SLOC, не так уж много за три недели.
Ну и еще, запомнилось чувство морального удовлетворения и гордости, которое я испытал, когда представлял заказчику полученные результаты.
Первым о полученных результатах докладывал немецкий коллега. Они решали задачу прямым перебором, и он долго рассказывал о том, сколько им для этого потребовалось недель непрерывных расчетов и сколько процессоров Pentium они задействовали параллельно.
Затем он представил полученный результат, но отметил, что он не может дать объяснение, почему получилось именно такое орбитальное построение – так рассчитали компьютеры.
Свое выступление я начал словами: «Мы получили очень похожий результат, только он на 15% лучше и я вам сейчас объясню, почему оптимальное орбитальное построение должно быть именно таким».
В конце концов, мы с немецким коллегой объединили наши результаты и опубликовали их в совместном докладе на международной конференции по навигации.
А теперь слово вам, уважаемые коллеги!
Не жадничаем. Не скромничаем. Делимся в комментариях своими историями успеха.
Автор:






