Предисловие
В качестве дополнения к моей недавней статье хотелось бы также поговорить о теме MU (Multi User) MIMO. Есть у мною уже упомянутого профессора Хаардта одна очень известная статья, где он вместе со своими коллегами предлагает алгоритм разделения пользователей по нисходящему каналу (Down Link) на основе линейных методов, а именно блоковой диагонализации (Block Diagonalization) канала. Статья имеет внушающее количество цитирований, а также является краеугольной публикацией для одного из заданий экзамена. Поэтому почему бы и не разобрать основы предлагаемого алгоритма?
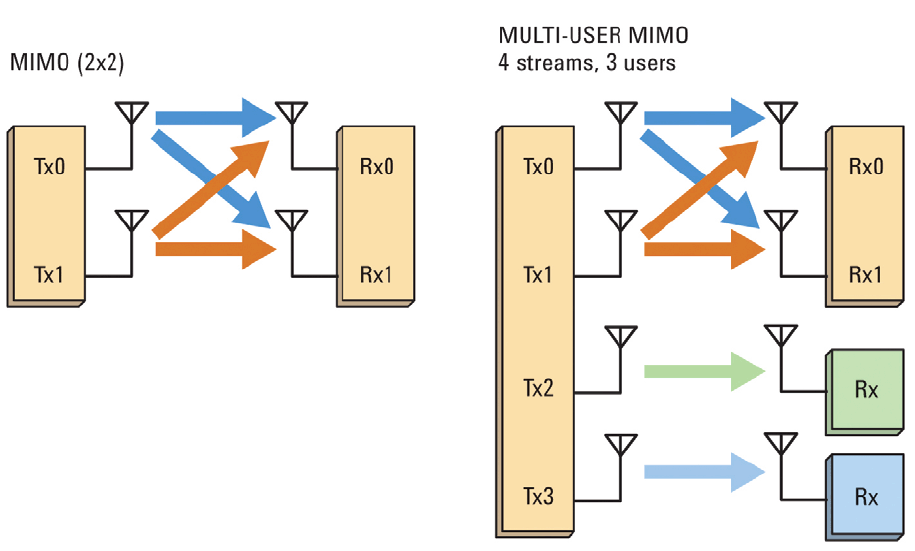
(ссылка на источник иллюстрации)
Постановка задачи
Во-первых, давайте определимся в какой области в тематике MIMO мы будем сейчас работать.
Условно, все методы передачи в рамках MIMO технологии можно разделить на две основные группы:
- Пространственное разнесение (spatial diversity).
Основной целью является увеличение помехоустойчивости передачи. Пространственные каналы, если упрощенно, дублируют друг друга, за счет чего мы получаем лучшее качество передачи.
Примеры:
— Блочные коды (например, схема Аламути);
— Коды, основанные на алгоритме Витерби.
- Пространственное мультиплексирование (spatial multiplexing).
Основной целью является увеличение скорости передачи. Мы уже обсуждали в предыдущей статье, что при определенных условиях канал MIMO можно рассматривать как ряд параллельных каналов SISO. Собственно говоря, это и есть центральная идея пространственного мультиплексирования: добиться максимального количества независимых информационных потоков. Главная проблема в данном случае — это подавление межканальной интерференции (inter-channel interference), для чего существуют несколько классов решений:
— горизонтальное разделение каналов;
— вертикальное (например, алгоритм V-BLAST);
— диагональное (например, алгоритм D-BLAST).
Но и это, конечно, не всё.
Идею пространственного мультиплексирования можно расширить: разделять не только каналы, но и пользователей (SDMA — Space Division Multiple Access).
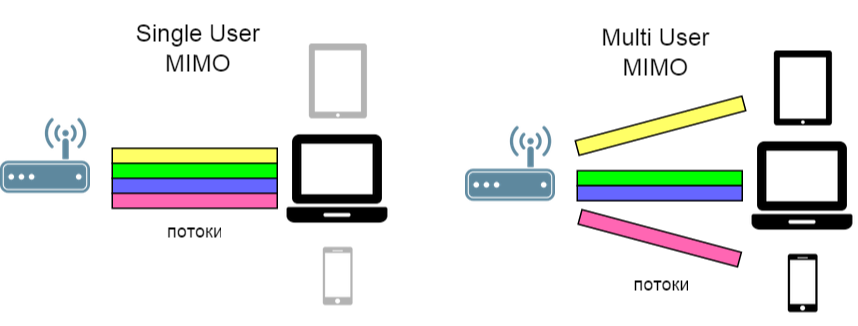
(ссылка на источник иллюстрации)
Следовательно, и бороться в этом случае уже нужно с интерференцией межпользовательской (inter-user interference). Именно для этого и был предложен алгоритм под названием Block diagonalization Zero-Forcing, который мы сегодня и рассматриваем.
Математическое описание
Начнем, как и прежде, с модели принятого сигнала (received signal). А точнее, покажем на схеме что куда и из чего происходит:

Канальная матрица в этом случае имеет вид:

при общем числе передающих антенн 

Важно:
Данный алгоритм может быть применён только при условии того, что количество передающих антенн больше или равно общему количеству приёмных антенн:Это условие напрямую влияет на свойства диагонализации.
Итак, модель принятых символов (сигналов) можно записать в векторном виде как:

Однако, интереснее посмотреть на формулу для конкретного пользователя:

Собственно говоря:
-
— это полезный сигнал для k-ого пользователя,
-
— это интерференция от других пользователей,
— аддитивный шум.
Вот мы и подошли к формулировке главной задачи:
Можно ведь найти такие матрицы
, чтобы интерференционная часть обращалась в ноль!
Этим мы и займемся.
Описание алгоритма
Описание проведем на примере, а в качестве иллюстрации я буду приводить скриншоты из первых рук, немного их комментируя.
Рассмотрим первого пользователя:

Проговорим основные шаги:
- Составляем некоторую матрицу
из канальных матриц всех остальных пользователей.
-
Раскладываем её методом SVD.
-
В матрице
находим шумовое подпространство (null-subspace) — матрицу
(т.е. всё что выходит за ранг матрицы
— обозначим его
).
-
Составляем из этой шумовой матрицы и её эрмитового сопряжения некоторую матрицу проекции
.
Идём дальше:

-
Теперь уже оригинальную часть канальной матрицы
перемножаем с полученной матрицей проекции
.
-
Раскладываем результат через SVD.
-
В матрице
выбираем
строк, где
— ранг
.
-
Транспонируем их и получаем матрицу
(или
— где как обозначают).
И так эта процедура будет повторяться для каждого пользователя. Не это ли магия математики: используя методы линейной алгебры, решаем вполне технические задачи!
Отметим, что на практике используются не только полученные матрицы пре-кодирования, но, и матрицы пост-обработки, и матрицы сингулярных значений (см. слайды). Последние, например, для балансировки мощности по уже знакомому нам алгоритму Water-pouring.
Моделируем алгоритм
Я думаю, не будет лишним провести небольшое моделирование, чтобы закрепить результат. Для этого будем использовать Python 3, а именно:
import numpy as np для основных расчетов, и:
import pandas as pd для отображения результата.
class ZeroForcingBD:
def __init__(self, H, Mrs_arr):
Mr, Mt = np.shape(H)
self.Mr = Mr
self.Mt = Mt
self.H = H
self.Mrs_arr = Mrs_arr
def __routines(self, H, mr, shift):
# used in self.process() - See example above for illustration
# inputs:
# H - the whole channel matrix
# mr - number of receive antennas of the i-th user
# shift - how much receive antennas were considered before
# outputs:
# Uidx, Sigmaidx, Vhidx - SVD decomposition of the H_iP_i
# d - rank of the hat H_i
# Hidx - H_i (channel matrix for the i-th user)
# r - rank of the H_i
Hidx = H[0+shift:mr+shift,:] # H_i (channel matrix for the i-th user)
r = np.linalg.matrix_rank(Hidx) # rank of the H_i
del_idx = [i for i in range(0+shift, mr+shift, 1)] # row indeces of H_i in H
H_hat_idx = np.delete(H, del_idx, 0) # hat H_i
d = np.linalg.matrix_rank(H_hat_idx) # rank of the hat H_i
U, Sigma, Vh = np.linalg.svd(H_hat_idx) # SVD
Vhn = Vh[d:, :] # null-subspace of V^H
Vn = np.matrix(Vhn).H # null-subspace of V
Pidx = np.dot(Vn, np.matrix(Vn).H) # projection matrix
Uidx, Sigmaidx, Vhidx = np.linalg.svd(np.dot(Hidx, Pidx)) # SVD of H_iP_i
return Uidx, Sigmaidx, Vhidx, d, Hidx, r
def process(self):
# used in self.obtain_matrices()
# outputs:
# F - whole filtering (pre-coding) matrix (array of arrays)
# D - whole demodulator (post-processing) matrix (array of arrays)
# H - the whole channel matrix (array of arrays)
shift = 0
H = self.H
F = []
D = []
Hs = []
for mr in self.Mrs_arr:
Uidx, Sigmaidx, Vhidx, d, Hidx, r = self.__routines(H, mr, shift)
Vhidx1 = Vhidx[:r,:] # signal subspace
Fidx = np.matrix(Vhidx1).H
F.append(Fidx)
D.append(Uidx)
Hs.append(Hidx)
shift = shift + mr
return F, D, Hs
def obtain_matrices(self):
# used to obtain pre-coding and post-processing matrices
# outputs:
# FF - whole filtering (pre-coding) matrix
# DD - whole demodulator (post-processing) matrix (array of arrays)
F, D, Hs = self.process()
FF = np.hstack(F)
# Home Task: calculation of the demodulator matrices :)
return FFПусть, у нас имеются 8 передающих антенн и 3 пользователя, у которых 3, 2 и 3 приёмных антенны соответственно:
Mrs_arr = [3,2,3]
# 1st user have 3 receive antennas, 2nd user - 2 receive antennas, 3d user - 3 receive antennas
Mr = sum(Mrs_arr) # total number of the receive antennas
Mt = 8 # total number of the transmitt antennas
H = (np.random.randn(Mr,Mt) + 1j*np.random.randn(Mr, Mt))/np.sqrt(2); #Rayleigh flat faded channel matrix (MrxMt)Инициализируем наш класс и применяем соответствующие методы:
BD = ZeroForcingBD(H, Mrs_arr)
F, D, Hs = BD.process()
FF = BD.obtain_matrices()Приводим к читабельному виду:
df = pd.DataFrame(np.dot(H, FF))
df[abs(df).lt(1e-14)] = 0И немного подрихтуем для наглядности (хотя можно и без этого):
print(pd.DataFrame(np.round(np.real(df),100)))
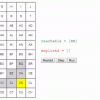
Должно получиться нечто такое:
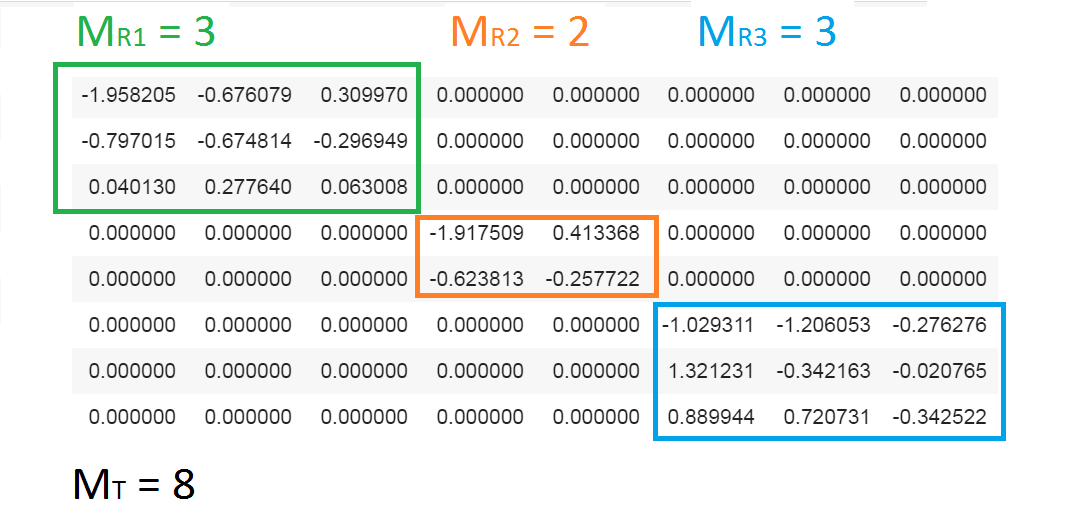
Собственно, вот они и блоки, вот она и диагонализация. И минимизация интерференции.
Такие дела.
Литература
- Spencer, Quentin H., A. Lee Swindlehurst, and Martin Haardt. "Zero-forcing methods for downlink spatial multiplexing in multiuser MIMO channels." IEEE transactions on signal processing 52.2 (2004): 461-471.
- Martin Haard "Robust Transmit Processing for Multi-User MIMO Systems"
P.S.
Преподавательскому составу и студенческой братии родной специальности передаю привет!
Автор: Владимир Фадеев