Развивая тему конспектов по магистерской специальности "Communication and Signal Processing" (TU Ilmenau), продолжить хотелось бы одной из основных тем курса "Adaptive and Array Signal Processing". А именно основами адаптивной фильтрации.
Для кого в первую очередь была написана эта статья:
1) для студенческой братии родной специальности;
2) для преподавателей, которые готовят практические семинары, но ещё не определились с инструментарием — ниже будут примеры на python и Matlab/Octave;
3) для всех, кто интересуется темой фильтрации.
Что можно найти под катом:
1) сведения из теории, которые я постарался оформить максимально сжато, но, как мне кажется, информативно;
2) примеры применения фильтров: в частности, в рамках эквалайзера для антенной решетки;
3) ссылки на базисную литературу и открытые библиотеки (на python), которые могут быть полезны для исследований.
В общем, добро пожаловать и давайте разбирать всё по пунктам.

Задумчивый человек на фото — знакомый многим, я думаю, Норберт Винер. Фильтр его имени мы, по большей части, и будем изучать. Однако, нельзя не упомянуть и о нашем соотечественнике — Андрее Николаевиче Колмогорове, чья статья 1941 года также внесла значительный вклад в развитие теории оптимальной фильтрации, которая даже в англоязычных источниках так и называется Kolmogorov-Wiener filtering theory.
Что рассматриваем?
Сегодня мы рассматриваем классический фильтр с конечной импульсной характеристикой (КИХ, FIR — finite impulse response), описать который можно следующей простой схемой (рис. 1).
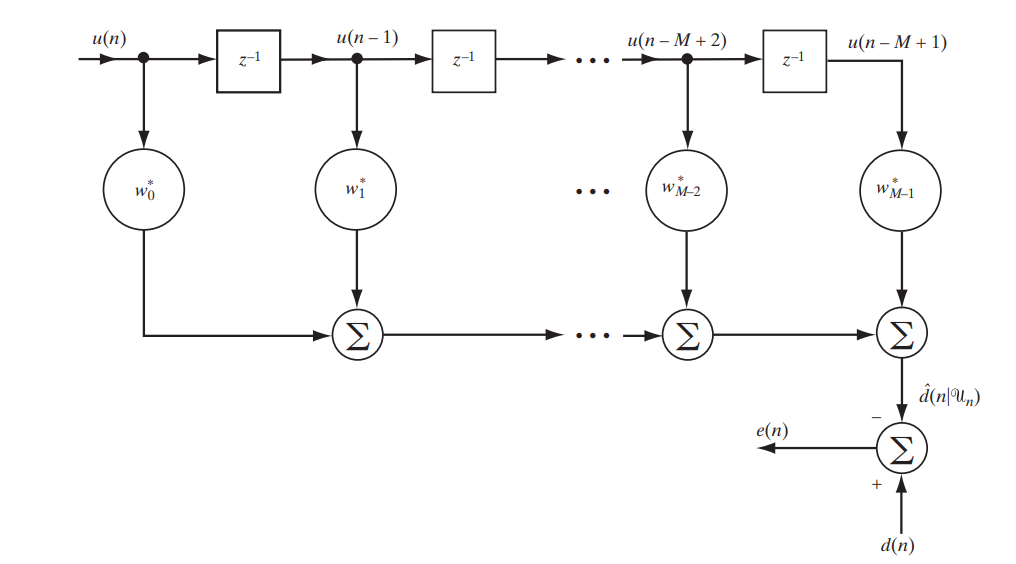
Рис.1. Схема КИХ-фильтра для изучения фильтра Винера.[1. c.117]
Запишем в матричном виде, что именно будет на выходе данного стенда:

Расшифруем обозначения:
— это разница (ошибка) между заданным и полученным сигналами
— это некоторый предварительно заданный сигнал (desired signal)
— это вектор отсчетов или, иными словами, сигнал на входе фильтра
— это сигнал на выходе фильтра
— это эрмитово сопряжение вектора коэффициентов фильтра — именно в их оптимальном подборе и кроется адаптивность фильтра
Наверное вы уже догадались, что стремиться мы будем к наименьшей разнице между заданным и отфильтрованным сигналом, то есть к наименьшей ошибке. А значит перед нами вырисовывается оптимизационная задача.
Что будем оптимизировать?
Оптимизировать, а точнее минимизировать мы будем не просто ошибку, среднюю квадратичную ошибку (MSE — Mean Sqared Error):

где 

Квадрат в данном случае очень приятен, так как он означает, что перед нами задача выпуклого программирования (я нагуглил только такой аналог английскому convex optimization), что, в свою очередь, подразумевает единственный экстремум (в нашем случае минимум).
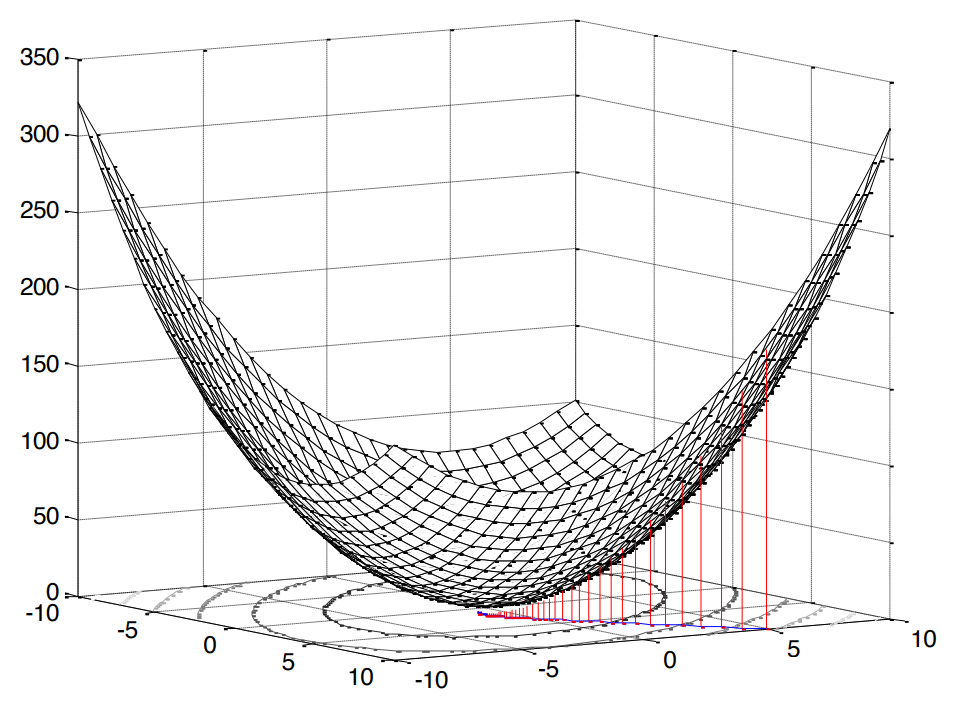
Рис.2. Поверхность средней квадратичной ошибки.
У нашей функции ошибки есть каноническая форма [1, c.121]:

где 


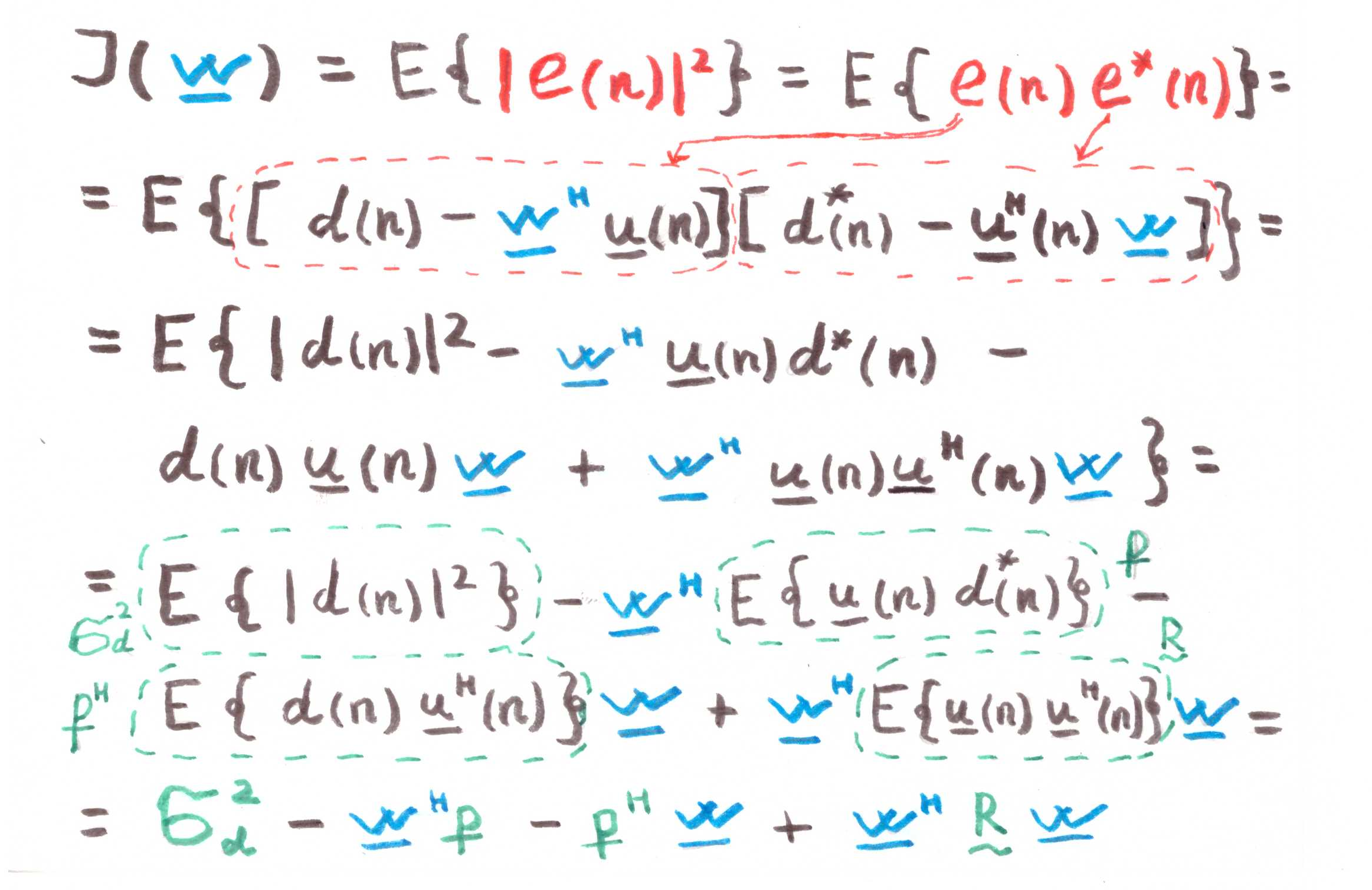
Как мы уже отметили выше, если мы ведем речь о выпуклом программировании, то и экстремум (минимум) у нас будет один. А значит, чтобы найти минимальное значение функции издержек (минимальную среднюю квадратичную ошибку), достаточно найти тангенс угла наклона касательной или, иначе говоря, частную производную по нашей исследуемой переменной:

В оптимальном случае (

Собственно, вот она, наша печка, от которой мы будем плясать дальше: перед нами система линейных уравнений.
Как будем решать?
Нужно отметить сразу, что оба решения, которые мы рассмотрим ниже, в данном случае являются теоретическими и учебными, так как 

Аналитическое решение
Решать эту задачу можно, так сказать, в лоб — с помощью обратных матриц:

Такое выражение называется уравнением Винера-Хопфа (Wiener–Hopf equation) — оно нам ещё пригодится в качестве некого эталона.
Конечно, если быть совсем дотошным, то, наверное, правильнее было бы записать это дело в общем виде, т.е. не с
, а с
(псевдо-инвертирование):

Однако, автокорреляционная матрица не может быть не-квадратной или сингулярной, поэтому вполне справедливо считаем, что никакого противоречия нет.
Из данного уравнения аналитически можно вывести, чему будет равняться минимальное значение функции издержек (т.е. в нашем случае MMSE — minimum mean square error):

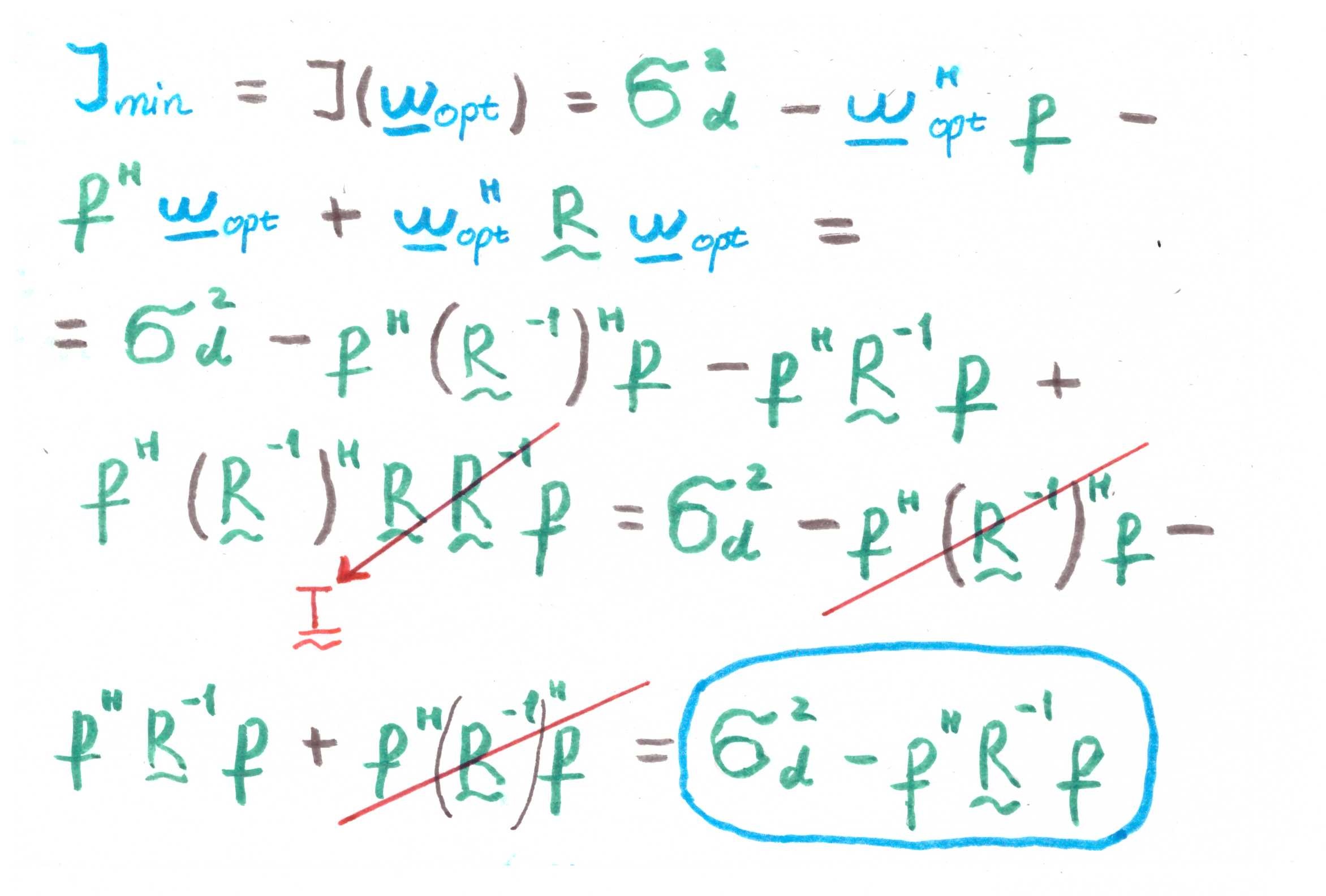
Хорошо, одно решение есть.
Решение итеративным методом
Однако, да, решать систему линейных уравнений можно и без инвертирования автокорреляционной матрицы — итеративно (to save computations). Для этой цели рассмотрим родной и понятный метод градиентного спуска (method of steepest/gradient descent).
Суть алгоритма можно свести к следующему:
- Выставляем искомую переменную в какое-то значение по умолчанию (например,
)
- Выбираем некоторый шаг
(как именно выбираем, мы поговорим ниже).
- И далее, как бы, спускаемся вниз по нашей исходной поверхности (в нашем случае, это поверхность MSE) с заданным шагом
и определенной скоростью, определяемой величиной градиента.
Отсюда и название: gradient — градиентный или steepest — пошаговый descent — спуск.
Градиент в нашем случае уже известен: по сути, мы нашли его, когда дифференцировали функцию издержек (поверхность же вогнутая, сравните с [1, с. 220]). Запишем как будет выглядеть формула для итеративного обновления искомой переменной (коэффициентов фильтра) [1, с. 220]:
![Оптимальная линейная фильтрация: от метода градиентного спуска до адаптивных фильтров - 32 mathbf{w}(n+1)=mathbf{w}(n) - mu [-mathbf{p} + mathbf{R}mathbf{w}(n)] qquad (8)](https://www.pvsm.ru/images/2019/07/20/optimalnaya-lineinaya-filtraciya-ot-metoda-gradientnogo-spuska-do-adaptivnyh-filtrov-32.svg)
где 
Теперь давайте поговорим о выборе величины шага.
Перечислим очевидные предпосылки:
- шаг не может быть отрицательным или нулевым
- шаг не должен быть слишком большим, иначе алгоритм не сойдется (будет, как бы, перескакивать от края до края, не попадая в экстремум)
- шаг, конечно, может быть очень маленьким, но и это тоже не совсем желательно — алгоритм будет тратить большее количество времени
Относительно фильтра Винера ограничения, конечно, уже были давно найдены [1, с.222-226]:

где 

Кстати говоря, собственные числа и вектора — это отдельная интересная тема в контексте линейной фильтрации. Под это дело есть даже целый Eigen filter (см. Приложение 1).
Но и это, к счастью, не все. Есть и оптимальное, адаптивное решение:

где 

Окей, под второе решение мы тоже подготовили почву.
А нельзя ли на примерах?
Наглядности ради проведем небольшое моделирование. Использовать будем Python 3.6.4.
Скажу сразу, данные примеры — это часть одного из домашних заданий, каждое из которых предлагается студентам для решения в течении двух недель. Часть я переписал под python (в целях популяризации языка среди радиоинженеров). Возможно, вы встретите в Сети ещё какие-то варианты от других бывших студентов.
import numpy as np
import matplotlib.pyplot as plt
from scipy.linalg import toeplitz
def convmtx(h,n):
return toeplitz(np.hstack([h, np.zeros(n-1)]),
np.hstack([h[0], np.zeros(n-1)]))
def MSE_calc(sigmaS, R, p, w):
w = w.reshape(w.shape[0], 1)
wH = np.conj(w).reshape(1, w.shape[0])
p = p.reshape(p.shape[0], 1)
pH = np.conj(p).reshape(1, p.shape[0])
MSE = sigmaS - np.dot(wH, p) - np.dot(pH, w) + np.dot(np.dot(wH, R), w)
return MSE[0, 0]
def mu_opt_calc(gamma, R):
gamma = gamma.reshape(gamma.shape[0], 1)
gammaH = np.conj(gamma).reshape(1, gamma.shape[0])
mu_opt = np.dot(gammaH, gamma) / np.dot(np.dot(gammaH, R), gamma)
return mu_opt[0, 0]Наш линейный фильтр мы применим для задачи выравнивания канала (channel equalization), основной целью которого является нивелировать различные воздействия этого самого канала на полезный сигнал.
Исходники одним файлом можно скачать здесь или здесь (да, было у меня такое хобби — Википедию править).
Модель системы
Допустим, есть антенная решетка (её мы уже рассматривали в статье про MUSIC).

Рис. 3. Ненаправленная линейная антенная решетка (ULAA — uniform linear antenna array) [2, с. 32].
Определим исходные параметры решетки:
M = 5 # количество элементов решетки (number of sensors)В данной работе мы будем рассматривать что-то вроде широкополосного канала с замираниями, характерной чертой которого является многолучевое распространение. Для таких случаев обычно применяют подход, при котором каждый луч моделируется с помощью задержки определенной величины (рис. 4).
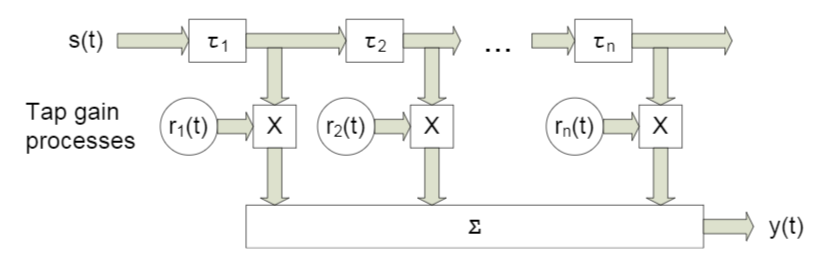
Рис. 4. Модель широкополосного канала при n фиксированных задержках.[3, c. 29]. Как вы понимаете, конкретные обозначения роли не играют — далее мы будем использовать немного другие.
Модель принимаемого сигнала для одного сенсора выразим следующим образом:

В данном случае 


Для нескольких сенсоров формула примет вид:

где 






Предположим, что каждый сенсор принимает сигнал тоже с какой-то задержкой, в силу падения волны под каким-то углом. Матрица 
h = np.array([0.722-1j*0.779, -0.257-1j*0.722, -0.789-1j*1.862])
L = len(h)-1 # number of signal sources
H = convmtx(h,M-L)
print(H.shape)
print(H)Выводом будет:
>>> (5, 3)
>>> array([[ 0.722-0.779j, 0. +0.j , 0. +0.j ],
[-0.257-0.722j, 0.722-0.779j, 0. +0.j ],
[-0.789-1.862j, -0.257-0.722j, 0.722-0.779j],
[ 0. +0.j , -0.789-1.862j, -0.257-0.722j],
[ 0. +0.j , 0. +0.j , -0.789-1.862j]])Далее зададим исходные данные для полезного сигнала и шума:
sigmaS = 1 # мощность полезного сигнала (the signal's s(n) power)
sigmaN = 0.01 # мощность шума (the noise's n(n) power)Теперь переходим к корреляциям.
Rxx = (sigmaS)*(np.dot(H,np.matrix(H).H))+(sigmaN)*np.identity(M)
p = (sigmaS)*H[:,0]
p = p.reshape((len(p), 1))
Найдем решение по Винеру:
# Solution of the Wiener-Hopf equation:
wopt = np.dot(np.linalg.inv(Rxx), p)
MSEopt = MSE_calc(sigmaS, Rxx, p, wopt)Теперь перейдем к методу градиентного спуска.
Найдем наибольшее собственное число, чтобы из неё потом вывести верхнюю границу шага (см. формулу (9)):
lamda_max = max(np.linalg.eigvals(Rxx))Теперь зададим некоторый массив шагов, которые будут составлять определенную долю от максимального:
coeff = np.array([1, 0.9, 0.5, 0.2, 0.1])
mus = 2/lamda_max*coeff # different step sizesОпределим максимальное количество итераций:
N_steps = 100Запускаем алгоритм:
MSE = np.empty((len(mus), N_steps), dtype=complex)
for mu_idx, mu in enumerate(mus):
w = np.zeros((M,1), dtype=complex)
for N_i in range(N_steps):
w = w - mu*(np.dot(Rxx, w) - p)
MSE[mu_idx, N_i] = MSE_calc(sigmaS, Rxx, p, w)Теперь сделаем то же самое, но уже для адаптивного шага (формула (10)):
MSEoptmu = np.empty((1, N_steps), dtype=complex)
w = np.zeros((M,1), dtype=complex)
for N_i in range(N_steps):
gamma = p - np.dot(Rxx,w)
mu_opt = mu_opt_calc(gamma, Rxx)
w = w - mu_opt*(np.dot(Rxx,w) - p)
MSEoptmu[:, N_i] = MSE_calc(sigmaS, Rxx, p, w)Получить должны нечто такое:
x = [i for i in range(1, N_steps+1)]
plt.figure(figsize=(5, 4), dpi=300)
for idx, item in enumerate(coeff):
if item == 1:
item = ''
plt.loglog(x, np.abs(MSE[idx, :]),
label='$mu = '+str(item)+'mu_{max}$')
plt.loglog(x, np.abs(MSEoptmu[0, :]),
label='$mu = mu_{opt}$')
plt.loglog(x, np.abs(MSEopt*np.ones((len(x), 1), dtype=complex)),
label = 'Wiener solution')
plt.grid(True)
plt.xlabel('Number of steps')
plt.ylabel('Mean-Square Error')
plt.title('Steepest descent')
plt.legend(loc='best')
plt.minorticks_on()
plt.grid(which='major')
plt.grid(which='minor', linestyle=':')
plt.show()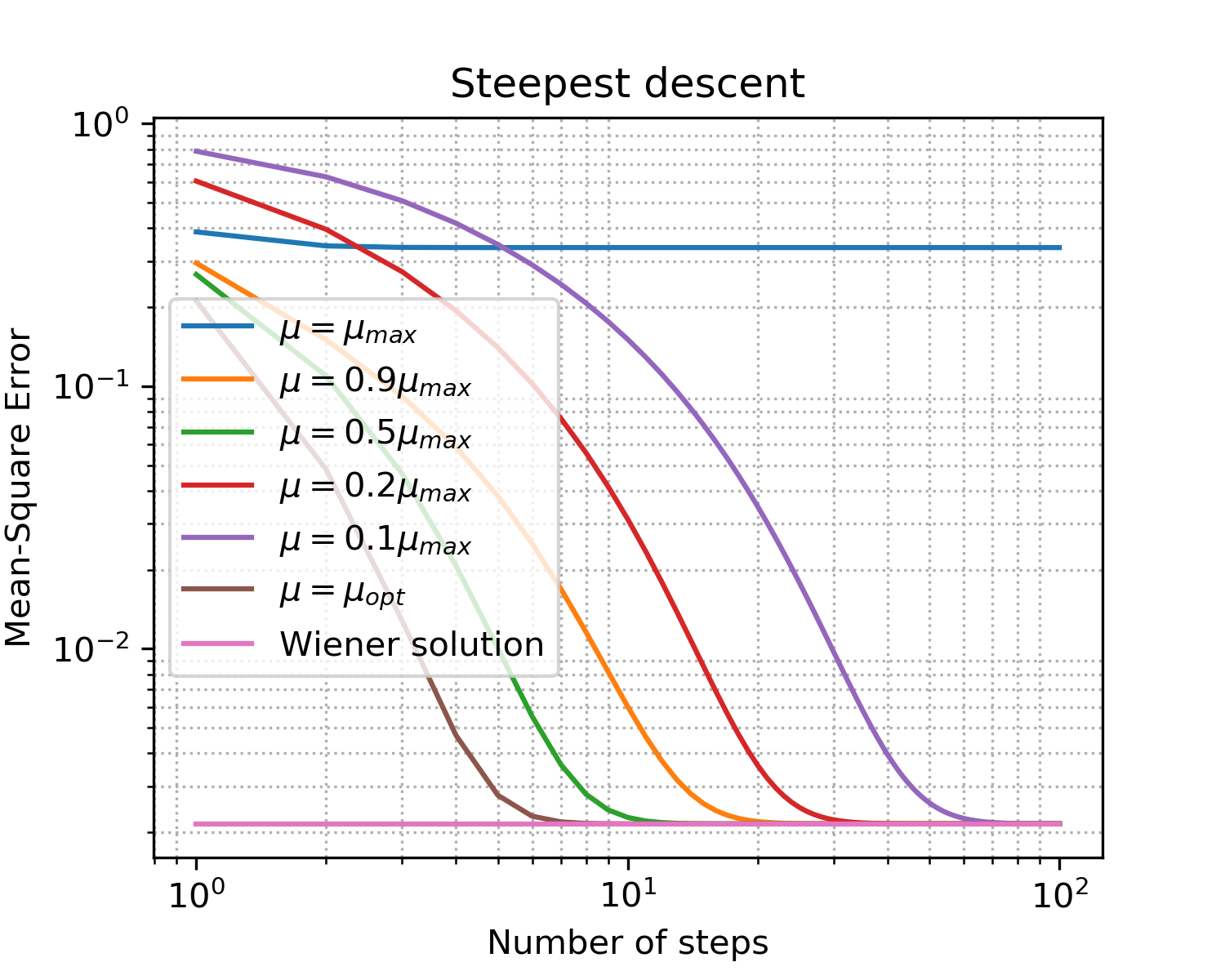
Рис. 5. Кривые обучения (learning curves) для шагов разных размеров.
Закрепления ради проговорим основные моменты по градиентному спуску:
- как и ожидалось, оптимальный шаг дает самую быструю сходимость;
- больше не значит лучше: превысив верхнюю границу мы вообще не достигли сходимости.
Вот мы и нашли оптимальный вектор коэффициентов фильтра, который будет наилучшим образом нивелировать влияния канала — обучили эквалайзер.
А есть что-то более близкое к реальности?
Конечно! Мы уже несколько раз проговорили, что сбор статистики (т.е. вычисление корреляционных матриц и векторов) в real-time системах — это далеко не всегда доступная роскошь. Однако, человечество приспособилось и к этим сложностям: вместо подхода детерминированного на практике используются подходы адаптивные. Разделить их можно на две большие группы [1, c. 246]:
- вероятностные (stochastic) (например, SG — Stochastic Gradient)
- и на основе метода наименьших квадратов (например, LMS — Least Mean Squares или RLS — Recursive Least Squares)
Тема адаптивных фильтров неплохо представлена в рамках open-source сообщества (примеры для python):
Во втором примере мне особенно нравится документация. Однако, будьте внимательны! Когда я тестировал пакет padasip, я столкнулся со сложностями в обработке комплексных чисел (по дефолту там подразумеваются float64). Возможно, такие же проблемы могут возникнуть и при работе с какими-то другими реализациями.
Алгоритмы, конечно же, имеют свои достоинства и недостатки, сумма которых и определяет область применения алгоритма.
Коротко взглянем на примеры: рассматривать будем три уже упомянутых нами алгоритма SG, LMS и RLS (моделировать будем на языке MATLAB — каюсь, заготовки уже были, а переписывать всё на питон единообразия ради… ну...).
Описание алгоритмов LMS и RLS можно подсмотреть, например, в доке по padasip.
Основное отличие от градиентного спуска состоит в изменяемом градиенте:
![Оптимальная линейная фильтрация: от метода градиентного спуска до адаптивных фильтров - 57 mathbf{w}[n]=mathbf{w}[n-1] + mu left(mathbf{hat{p}}[n] - mathbf{hat{R}}_{xx}[n]mathbf{w}[n-1]right)](https://www.pvsm.ru/images/2019/07/20/optimalnaya-lineinaya-filtraciya-ot-metoda-gradientnogo-spuska-do-adaptivnyh-filtrov-57.svg)
при
![Оптимальная линейная фильтрация: от метода градиентного спуска до адаптивных фильтров - 58 mathbf{hat{R}}_{xx}[n]=frac{1}{n}left( (n-1) mathbf{hat{R}}_{xx}[n-1] + mathbf{x}[n]mathbf{x}[n]^Hright)](https://www.pvsm.ru/images/2019/07/20/optimalnaya-lineinaya-filtraciya-ot-metoda-gradientnogo-spuska-do-adaptivnyh-filtrov-58.svg)
![Оптимальная линейная фильтрация: от метода градиентного спуска до адаптивных фильтров - 59 mathbf{hat{p}}[n]=frac{1}{n}left( (n-1) mathbf{hat{p}}[n-1] + mathbf{x}[n]d[n]^*right)](https://www.pvsm.ru/images/2019/07/20/optimalnaya-lineinaya-filtraciya-ot-metoda-gradientnogo-spuska-do-adaptivnyh-filtrov-59.svg)
1) Случай, аналогичный рассмотренному выше.
Исходники можно скачать здесь.

Рис. 6. Кривые обучения (learning curves) для LMS, RLS и SG.
Сразу можно отметить, что при своей относительной простоте алгоритм LMS может в принципе и не прийти к оптимальному решению при относительно большом шаге. Самый быстрый результат даёт RLS, но и он может засбоить при относительно небольшом факторе забывания (forgetting factor). Пока молодцом держится SG, но давайте посмотрим на другой пример.
2) Случай, когда канал меняется во времени.
Исходники можно скачать здесь.
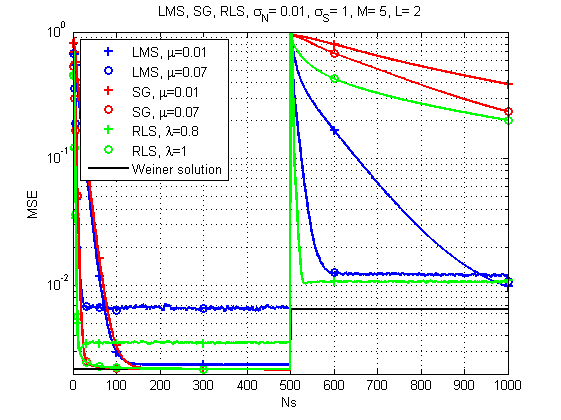
Рис. 7. Кривые обучения (learning curves) для LMS, RLS и SG (канал изменяется во времени).
А вот тут картина уже гораздо интересней: при резком изменении отклика канала самым надежным решением уже кажется LMS. Кто бы мог подумать. Хотя и RLS при правильном forgetting factor тоже обеспечивает приемлемый результат.
Да, конечно каждый алгоритм имеет свою определенную вычислительную сложность, однако по моим замерам моя старенькая машина справляется с одним ансамблем примерно за 120 мкс в итерацию в случае с LMS и SG и примерно за 250 мкс в итерацию в случае RLS. То есть разница, в общем-то, сравнимая.
А на этом у меня сегодня всё. Спасибо всем, кто заглянул!
Литература
-
Haykin S. S. Adaptive filter theory. – Pearson Education India, 2005.
-
Haykin, Simon, and KJ Ray Liu. Handbook on array processing and sensor networks. Vol. 63. John Wiley & Sons, 2010. pp. 102-107
-
Arndt, D. (2015). On Channel Modelling for Land Mobile Satellite Reception (Doctoral dissertation).
Приложение 1
Основная цель такого фильтра — это максимизировать отношение сигнал-шум (SNR — Signal-to-Noise Ratio).

Но судя по наличию в расчетах корреляций, это тоже больше теоретический конструкт, нежели практическое решение.
Автор: ritchie_kyoto


