Всем привет! Это небольшой рассказ про то, как команда Центра компетенции больших данных и искусственного интеллекта в ЛАНИТ оптимизировала работу банкоматной сети. Упор в статье сделан не на описание подбора параметров и выбор лучшего алгоритма прогнозирования, а на рассмотрение концепции нашего подхода к решению поставленной задачи. Кому интересно, добро пожаловать под кат.

источник
Банки теряют довольно много денег из-за того, что они просто лежат в банкоматах. Вместо этого деньги можно было бы успешно вложить и получать доход. Сегодня крупные банки с сильными аналитическими центрами имеют свои решения для того, чтобы рассчитать количество купюр и время, на которое их нужно заложить в банкоматы до следующей инкассации. Небольшие же игроки, не имея таких решений, просто ориентируются на средние значения, полученные в ходе предыдущих поездок инкассаторов.
Таким образом, формальная постановка задачи выглядит так.
На входе:
- есть история снятия/приема наличности в банкоматах (в нашем случае это были данные за полтора года);
- стоимость потерь от нахождения денег в банкоматах (от простаивающих запасов) зависит от ставки рефинансирования (параметр q); стоимость можно оценить как
, где S — сумма, X— количество дней;
- стоимость поездки инкассаторов, si (меняется со временем и зависит от местоположения банкомата и маршрута инкассаторов).
На выходе ожидается:
- система рекомендаций по количеству купюр и времени, на которое их нужно заложить;
- экономический эффект от предлагаемого решения.
Разработка велась совместно с @vladbalv, от которого поступило множество предложений, в том числе ключевых, которые легли в основу описываемого решения.
Общая идея основана на нахождении минимума затрат как функции от количества дней между инкассациями. Для объяснения конечного решения можно сначала рассмотреть упрощенный вариант — в предположении, что сумма снимаемых денег не меняется изо дня в день и равна S, и что она только убывает. В таком случае сумма денег в банкомате является убывающей арифметической прогрессией.
Предположим, что в день снимают S руб. Помимо суммы снятий, введем также переменную X — число дней между инкассациями, меняя которую будем дальше искать минимум затрат банка. Логично, что сумма, которую выгоднее всего положить в банкомат, зная, что инкассация будет через X дней это S*X. При таком подходе за день до инкассации в банкомате будет находиться S руб., за два дня — 2*S руб., за три дня — 3*S руб. и т. д. Другими словами, наш ряд можно рассматривать, двигаясь от конца к началу, тогда это будет возрастающая арифметическая прогрессия. Поэтому за период между двумя инкассациями в банкомате будет лежать (S+S*X)/2 руб. Теперь, исходя из ставки рефинансирования, остаётся посчитать стоимость простаивающих запасов этой суммы за X дней и дополнительно прибавить стоимость совершённых инкассаторских поездок. Если между инкассациями X дней, то за n дней будет совершено ![Прикручиваем ИИ: оптимизация работы банкоматов - 3 $[frac{n}{X}]+1$](https://www.pvsm.ru/images/2021/04/20/prikruchivaem-ii-optimizaciya-raboty-bankomatov-3.svg)
![Прикручиваем ИИ: оптимизация работы банкоматов - 4 $[frac{n}{X}]$](https://www.pvsm.ru/images/2021/04/20/prikruchivaem-ii-optimizaciya-raboty-bankomatov-4.svg)
Таким образом, получившаяся функция выглядит так:
где:
- S — сумма снятий, руб./день,
- X — количество дней между инкассациями,
- n — рассматриваемый период в днях,
- q — ставка рефинансирования,
- si — стоимость инкассации.
Однако в реальности каждый день снимают разные суммы, поэтому у нас есть ряд снятий/внесений купюр, каждый день этот ряд пополняется новыми значениями. Если это учесть, функция примет следующий вид:
Что такое убывающие и возрастающие суммы: в зависимости от того, больше кладут или больше снимают, есть купюры, по которым сумма в банкомате накапливается, а есть купюры, по которым сумма в банкомате убывает. Таким образом формируются возрастающие и убывающие суммы купюр. В реализации было сделано три ряда: incr_sums — возрастающие купюры, decr_sums — убывающие купюры и withdrawal_sums — ряд сумм выдач банкомата (там присутствуют купюры, которые идут только на выдачу).
Также важный момент: если сумма возрастающая, то нам не нужно закладывать целиком всю сумму целого ряда, это необходимо делать только для убывающих сумм, поскольку они должны полностью исчезнуть к концу периода инкассации. Для возрастающих сумм мы решили закладывать сумму на три дня в качестве подушки безопасности, если что-то пойдёт не так.
Помимо прочего, чтобы применить описанную функцию, нужно учесть следующие моменты.
- Самое главное, сложное, и интересное — в момент инкассации мы не знаем, какие это будут суммы, их нужно прогнозировать (об этом ниже).
- Банкоматы бывают следующих типов:
○ только на внос/вынос,
○ на внос и вынос одновременно,
○ на внос и вынос одновременно + ресайклинг (за счёт ресайклинга у банкомата есть возможность выдавать купюры, которые в него вносят другие клиенты). - Описанная функция также зависит от n — количества рассматриваемых дней. Если подробнее рассмотреть эту зависимость на реальных примерах, то получится следующая картинка:
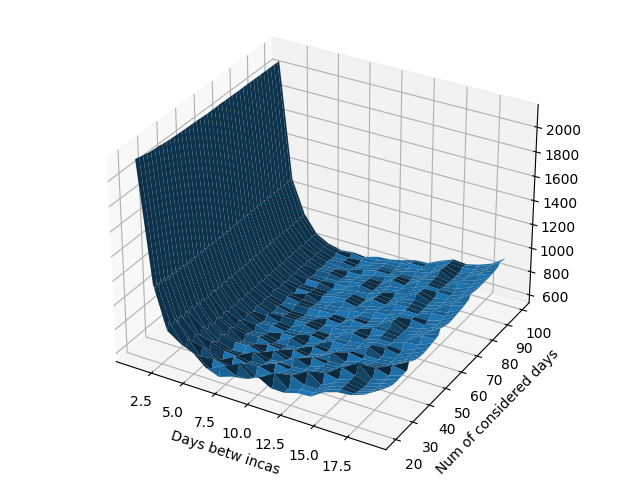
Рис. 1. Значения функции TotalCost в зависимости от X (Days betw incas) и n (Num of considered days)
Чтобы избавиться от n, можно воспользоваться простым трюком — просто разделить значение функции на n. При этом мы усредняем и получаем среднюю величину стоимости затрат в день. Теперь функция затрат зависит только от количества дней между инкассациями. Это как раз тот параметр, по которому мы будем её минимизировать.
Учитывая вышесказанное, реальная функция будет иметь следующий шаблон:
TotalCost(n, x, incr_sums, decr_sums, withdrawal_sums, si), где
- x —максимальное количество дней между инкассациями
- n — количество дней, которые отслеживаем, то есть мы смотрим последние n значений подаваемых на вход временных рядов (как написано выше, функция не зависит от n, этот параметр добавлен, чтобы можно было экспериментировать с длиной подаваемого временного ряда)
- incr_sums — ряд спрогнозированных сумм по купюрам только на внос,
- decr_sums — ряд спрогнозированных сумм по купюрам только на вынос,
- withdrawal_sums — ряд спрогнозированных сумм выдач банкомата (т.е. здесь сумма по купюрам in минус сумма по out), заполняется 0 для всех банкоматов кроме ресайклинговых,
- si — стоимость инкассации.
Функция проходит непересекающимся окном величиной X по входным рядам и считает суммы внесенных денег внутри окна. В отличие от первоначальной функции сумма арифметической прогрессии здесь превращается в обычную сумму (это та сумма, которая была заложена при инкассации). Далее внутри окна в цикле по дням происходит кумулятивное суммирование/вычитание сумм, которые ежедневно клались/снимались из банкомата. Это делается для того, чтобы получить сумму, которая лежала в банкомате на каждый день.
Затем из полученных сумм при помощи ставки рефинансирования рассчитывается стоимость затрат на простаивающие запасы, а также в конце прибавляются затраты от инкассаторских поездок.
def process_intervals(n, x, incr_sums, decr_sums, withdrawal_sums):
# генератор количества сумм, которые
# остаются в банкомате на каждый день
# incr_sums — ряд возрастающих сумм
# decr_sums — ряд убывающих сумм
# withdrawal_sums — ряд сумм выдач банкомата (там присутствуют купюры, которые идут только на выдачу)
# заполняется 0 для всех банкоматов кроме ресайклинговых
# x — количество дней между инкассациями
# n — количество дней, которые отслеживаем
if x>n: return
for i in range(n//x):
decr_interval = decr_sums[i*x:i*x+x]
incr_interval = incr_sums[i*x:i*x+x]
withdrawal_interval = withdrawal_sums[i*x:i*x+x]
interval_sum = np.sum(decr_interval)
interval_sum += np.sum(withdrawal_interval[:3])
for i, day_sum in enumerate(decr_interval):
interval_sum -= day_sum
interval_sum += incr_interval[i]
interval_sum += withdrawal_interval[i]
yield interval_sum
# остаток сумм. Берется целый интервал.
# но yield только для остатка ряда
decr_interval = decr_sums[(n//x)*x:(n//x)*x+x]
incr_interval = incr_sums[(n//x)*x:(n//x)*x+x]
withdrawal_interval = withdrawal_sums[(n//x)*x:(n//x)*x+x]
interval_sum = np.sum(decr_interval)
interval_sum += np.sum(withdrawal_sums[:3])
for i, day_sum in enumerate(decr_interval[:n-(n//x)*x]):
interval_sum -= day_sum
interval_sum += incr_interval[i]
interval_sum += withdrawal_sums[i]
yield interval_sum
def waiting_cost(n, x, incr_sums, decr_sums, withdrawal_sums, si):
# incr_sums — ряд возрастающих сумм
# decr_sums — ряд убывающих сумм
# withdrawal_sums — ряд сумм выдач банкомата (там присутствуют купюры, которые идут только на выдачу)
# заполняется 0 для всех банкоматов кроме ресайклинговых
# si — стоимость инкассации
# x — количество дней между инкассациями
# n — количество дней, которое отслеживаем
assert len(incr_sums)==len(decr_sums)
q = 4.25/100/365
processed_sums = list(process_intervals(n, x, incr_sums, decr_sums, withdrawal_sums))
# waiting_cost = np.sum(processed_sums)*q + si*(x+1)*n//x
waiting_cost = np.sum(processed_sums)*q + si*(n//x) + si
# делим на n, чтобы получить среднюю сумму в день (не зависящее от количества дней)
return waiting_cost/n
def TotalCost (incr_sums, decr_sums, withdrawal_sums, x_max=14, n=None, si=2500):
# x — количество дней между инкассациями
# n — количество дней, которое отслеживаем
assert len(incr_sums)==len(decr_sums) and len(decr_sums)==len(withdrawal_sums)
X = np.arange(1, x_max)
if n is None: n=len(incr_sums)
incr_sums = incr_sums[-n:]
decr_sums = decr_sums[-n:]
withdrawal_sums = withdrawal_sums[-n:]
waiting_cost_sums = np.zeros(len(X))
for i, x in enumerate(X):
waiting_cost_sums[i] = waiting_cost(n, x, incr_sums, decr_sums, withdrawal_sums, si)
return waiting_cost_sumsТеперь применим эту функцию к историческим данным наших банкоматов и получим следующую картинку:
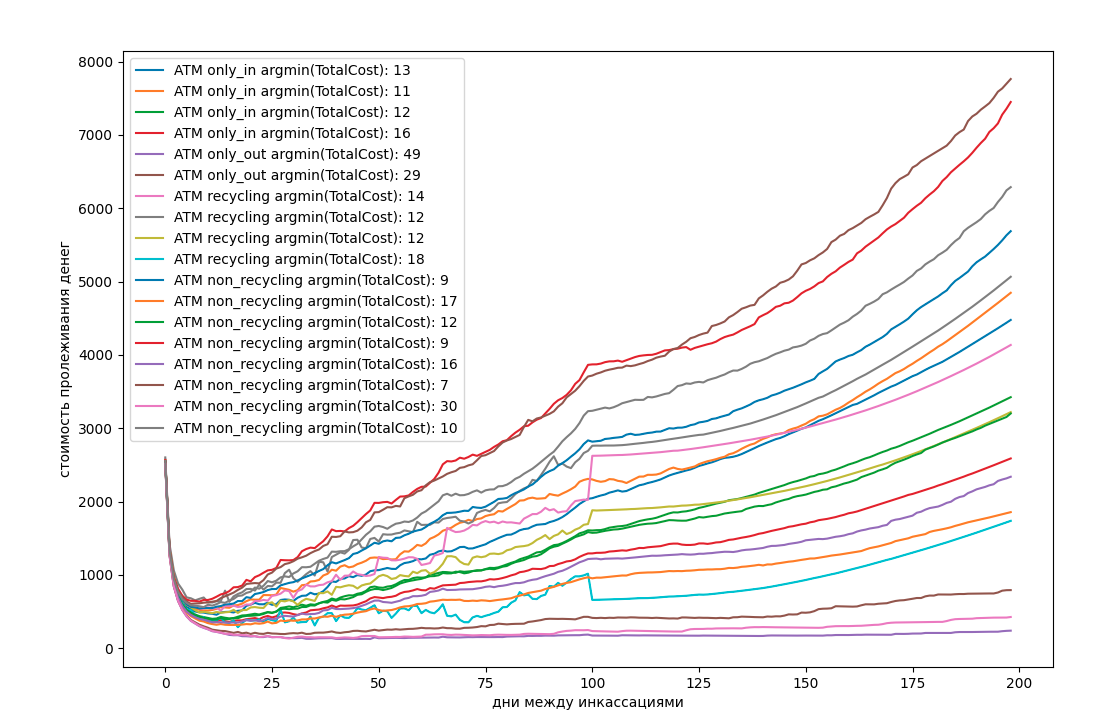
Рис. 2. Оптимальное количество дней между инкассациями
Резкие перепады на некоторых графиках объясняются провалами в данных. А то, что они произошли в одинаковое время, скорее всего можно объяснить техническими работами, на время которых банкоматы не работали.
Дальше нужно сделать прогноз снятия/зачисления наличности, применить к нему эту функцию, найти оптимальный день инкассации и загрузить определенное количество купюр по сделанному прогнозу.
В зависимости от суммы денег, находящейся в обращении (чем меньше денег проходит через банкомат, тем дольше оптимальный срок инкассации), меняется количество оптимальных дней между инкассациями. Бывают случаи, когда это количество больше 30. Прогноз на такой большой период времени будет слишком большой ошибкой. Поэтому вначале происходит оценка по историческим данным, если она меньше 14 дней (это значение было выбрано эмпирически, потому что оптимальное количество дней до инкассации у большинства банкоматов меньше 14 дней, а также потому, что чем дальше горизонт прогнозирования, тем больше его ошибка), то в дальнейшем для определения оптимального количества дней между инкассациями используется прогноз по временному ряду, иначе по историческим данным.
Подробно останавливаться на том, как делается прогноз снятий и зачислений не буду. Если есть интерес к этой теме, то можно посмотреть видеодоклад о решении подобной задачи исследователями из Сбербанка (Data Science на примере управления банкоматной сетью банка).
Из всего опробованного нами лучше всего показал себя CatBoostRegressor, регрессоры из sklearn немного отставали по качеству. Возможно, здесь не последнюю роль сыграло то, что после всех фильтраций и отделения валидационной выборки, в обучающей выборке осталось всего несколько сотен объектов.
Prophet показал себя плохо. SARIMA не стали пробовать, поскольку в видео выше о нем плохие отзывы.
Используемые признаки (всего их было 139, после признака приведено его обозначение на графике feature importance ниже)
- Временные лаги целевых значений переменной, lag_* (их количество можно варьировать, но мы остановились на 31. К тому же, если мы хотим прогнозировать не на день вперед, а на неделю, то и первый лаг смотрится не за вчерашний день, а за неделю назад. Таким образом, максимально далеко мы смотрели на 31+14=45 дней назад).
- Дельты между лагами, delta_lag*-lag*.
- Полиномиальные признаки от лагов и их дельт, lag_*^* (использовались только первые 5 лагов и их дельт, обозначались).
- День недели, месяца, номер месяца, weekday, day, month (категориальные переменные).
- Тригонометрические функции от временных значений из пункта выше, weekday_cos и т.д.
- Статистика (max, var, mean, median) для этого же дня недели, месяца, weekday_max, weekday_mean,… (брались только дни, находящиеся раньше рассматриваемого в обучающей выборке).
- Бинарные признаки выходных дней, когда банкоматы не работают, is_weekend
- Значения целевой переменной за этот же день предыдущей недели/месяца, y_prev_week, y_prev_month.
- Двойное экспоненциальное сглаживание + сглаживание по значениям целевой функции за те же дни предыдущих недели/месяца, weekday_exp_pred, monthday_exp_pred.
- Попробовали tsfresh, tsfresh+PCA, но потом отказались от этого, поскольку этих признаков очень много, а объектов в обучающей выборке у нас было мало.
Важность признаков для модели следующая (приведена модель для прогноза снятий купюры номиналом в 1000 руб. на один день вперед):
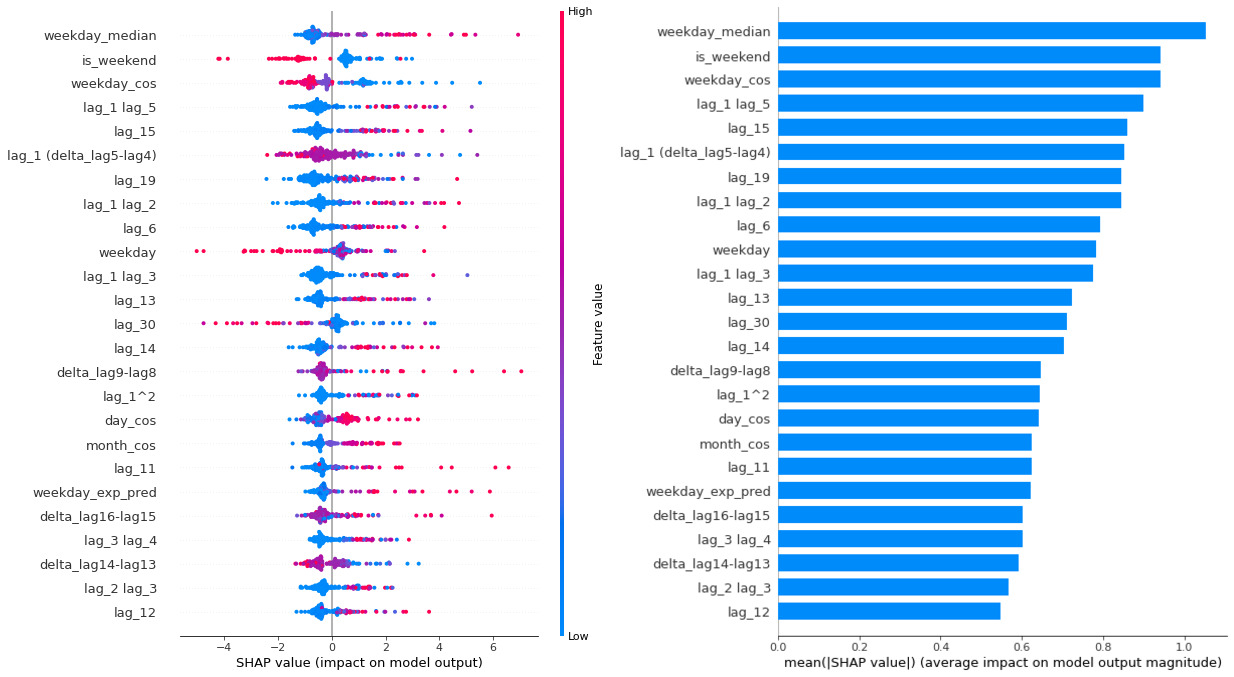
Рис. 3.Feature importance используемых признаков
Выводы по картинкам выше — наибольший вклад сделали лаговые признаки, дельты между ними, полиномиальные признаки и тригонометрические функции от даты/времени. Важно, что в своём прогнозе модель не опирается на какую-то одну фичу, а важность признаков равномерно убывает (правая часть графика на рис. 2).
Сам график прогноза выглядит следующим образом (по оси x отложены дни, по оси y количество купюр):
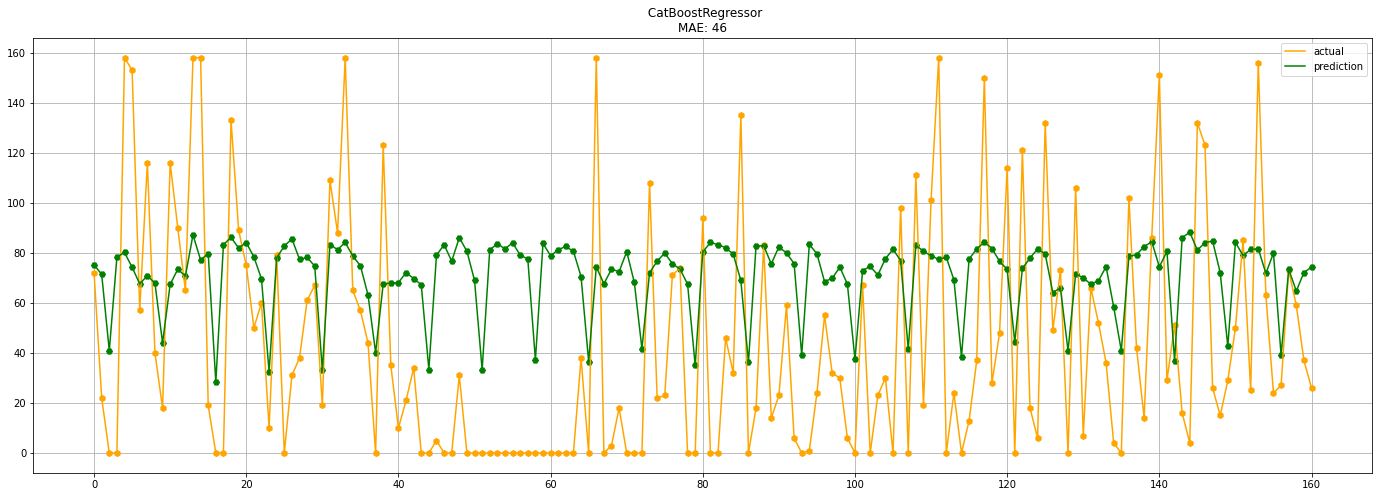
Рис. 4 — Прогноз CatBoostRegressor
По нему видно, что CatBoost всё же плохо выделяет пики (несмотря на то, что в ходе предварительной обработки выбросы были заменены на 95 перцентиль), но общую закономерность отлавливает, хотя случаются и грубые ошибки, как на примере провала в районе шестидесяти дней.
Ошибка по MAE там колеблется в примерном диапазоне от нескольких десятков до ста. Успешность прогноза сильно зависит от конкретного банкомата. Соответственно, величину реальной ошибки определяет номинал купюры.
Общий пайплайн работы выглядит следующим образом (пересчёт всех значений происходит раз в день).
- Для каждой купюры каждого atm на каждый прогнозируемый день своя модель (поскольку прогнозировать на день вперед и на неделю вперед — разные вещи и снятия по различным купюрам также сильно разнятся), поэтому на каждый банкомат приходится около 100 моделей.
- По историческим данным банкомата при помощи функции TotalCost находится оптимальное количество дней до инкассации.
- Если найденное значение меньше 14 дней, то следующий день инкассации и закладываемая сумма подбираются по прогнозу, который кладется в функцию TotalCost, иначе по историческим данным.
- На основе прогноза либо исторических данных снятий/внесений наличности рассчитывается сумма, которую нужно заложить (т.е. количество закладываемых купюр).
- В банкомат закладывается сумма + ошибка.
- Ошибка: при закладывании денег в банкомат необходимо заложить больше денег, оставив подушку безопасности, на случай, если вдруг люди дружно захотят обналичить свои сбережения (чтобы перевести их во что-то более ценное). В качестве такой суммы можно брать средние снятия за последние 2-3 дня. В усложнённом варианте можно прогнозировать снятия за следующие 2-3 дня и дополнительно класть эту сумму (выбор варианта зависит от качества прогноза на конкретном банкомате)
- Теперь с каждым новым днём приходят значения реальных снятий, и оптимальный день инкассации пересчитывается. Чем ближе день инкассации, полученный по предварительному прогнозу, тем больше реальных данных мы кладём в TotalCost вместо прогноза, и точность работы увеличивается.
Полученный профит мы посчитали следующим образом: взяли данные по снятиям/внесениям за последние три месяца и из этого промежутка по дню, как если бы к нам приходили ежедневные данные от банкоматов.
Для этих трёх месяцев рассчитали стоимость простаивающих запасов денег и инкассаторских поездок для исторических данных и для результата работы нашей системы. Получился профит. Усредненные за день величины приведены в таблице ниже (названия банкоматов заменены на латинские символы):
| atm | profit(relative) | ≈profit/day (руб.) |
| a | 0.61 | 367 |
| b | 0.68 | 557 |
| с | 0.70 | 470 |
| d | 0.79 | 552 |
| e | -0.30 | -66 |
| f | 0.49 | 102 |
| g | 0.41 | 128 |
| h | 0.49 | 98 |
| i | 0.34 | 112 |
| j | 0.48 | 120 |
| k | -0.01 | -2 |
| l | -0.43 | -26 |
| m | 0.127 | 34 |
| n | -0.03 | -4 |
| o | -0.21 | -57 |
| p | 0.14 | 24 |
| q | -0.21 | -37 |
Подходы и улучшения, которые интересно рассмотреть, но пока не реализованы на практике (в силу комплексности их реализации и ограниченности во времени):
- использовать нейронные сети для прогноза, возможно даже RL агента,
- использовать одну модель, просто подавая в неё дополнительный признак, отвечающий за горизонт прогнозирования в днях.
- построить эмбеддинги для банкоматов, в которых сагрегировать информацию о географии, посещаемости места, близости к магазинам/торговым центрам и т. д.
- если оптимальный день инкассации (на втором шаге пайплайна) превышает 14 дней, рассчитывать оптимальный день инкассации по прогнозу другой модели, например, Prophet, SARIMA, или брать для этого не исторические данные, а исторические данные за прогнозируемый период с прошлого года/усредненный за последние несколько лет.
- для банкоматов, у которых отрицательный профит, можно пробовать настраивать различные триггеры, при срабатывании которых работа с банкоматами ведется в старом режиме, либо инкассаторские поездки совершаются чаще/реже.
В заключение можно отметить, что временные ряды снятий/внесений наличности поддаются прогнозированию, и что в целом предложенный подход к оптимизации работы банкоматов является довольно успешным. При грубой оценке текущих результатов работы в день получается сэкономить около 2400 руб., соответственно, в месяц это — 72 тыс. руб., а в год — порядка 0,9 млн руб. Причём чем больше суммы денег, находящихся в обращении у банкомата, тем большего профита можно достичь (поскольку при небольших суммах профит нивелируется ошибкой от прогноза).
За ценные советы при подготовке статьи большая благодарность vladbalv и art_pro.
Спасибо за внимание!
Автор: ervin-x

![Прикручиваем ИИ: оптимизация работы банкоматов - 5 $TotalCost(S, X, n, q, si)=(S + S*X)/2*frac{q}{365}+si*([frac{n}{X}]+1)$](https://www.pvsm.ru/images/2021/04/20/prikruchivaem-ii-optimizaciya-raboty-bankomatov-5.svg)
![Прикручиваем ИИ: оптимизация работы банкоматов - 6 $TotalCost=sum_{i=1}^{n}Q_{i}*frac{q}{365} + si*([frac{n}{X}]+1) \ q - ставка, рефинансирования, \ n - количество, рассматриваемых, дней, \ X - количество, дней, между, инкассациями, \ Q_{i} - сумма, в, банкомате, на, iй, день,, Q_{i}=encash_{i} - sum_{k=[frac{i}{X}]*X}^{i}S_{k} \ S_{k} - изменение, суммы, в, банкомате, на, kй, день, \ encash_{i} - сумма, последней, на, iй, день, инкассации, \ encash_{i}=begin{cases} sum_{k=[frac{i}{X}]*X}^{([frac{i}{X}]*X+1)*X}S_{k}, ,,, если,сумма, убывающая \ \ sum_{k=[frac{i}{X}]*X}^{[frac{i}{X}]*X+3}S_{k}^{-}, ,,, если,сумма, возрастающая end{cases} \ S_{k}^{-} - сумма, снятий, за, kй, день \$](https://www.pvsm.ru/images/2021/04/20/prikruchivaem-ii-optimizaciya-raboty-bankomatov-6.svg)





