Как лучше обучать RNN для прогнозирования временных рядов?

Привет!

Два последних года я в рамках магистерской диссертации разбирался с тем, как лучше использовать рекуррентные нейронные сети для прогнозирования временных рядов, и теперь хочу поделиться моим опытом с сообществом.

Я разделил свой рассказ на несколько блоков:

• Что такое RNN

• Рекуррентные нейроны

• Методы обработки временных рядов

• Стратегии прогнозирования

• Добавление факторов в RNN

• Глобальные модели RNN

По ходу статьи я буду приводить выводы, которые основывал на научной литературе и экспериментах, проведенных в рамках моего исследования. Подробно описывать эксперименты в данной статье было бы слишком громоздко, поэтому приведу лишь основные параметры и схемы потока данных каждого из них:

Параметры экспериментов

Общие параметры

• Объект – 8 временных рядов, которые представляли цены закрытия акций российских и иностранных компаний с 2012 по 2021 год по дням.

• Длина входного вектора (inputsize) = 30 дней

• Прогнозный горизонт = 7 дней.

• Архитектура: Stacked RNN (LSTM-Dropout-Linear)

• Количество эпох: 40

• Кросс-валидация: expanding rolling window c 5 фолдами.

• Оптимизационная метрика: MAE

• Оптимизатор: adam

Эксперимент 1: Сравнительный анализ влияния методов обработки временных рядов на прогноз моделями RNN

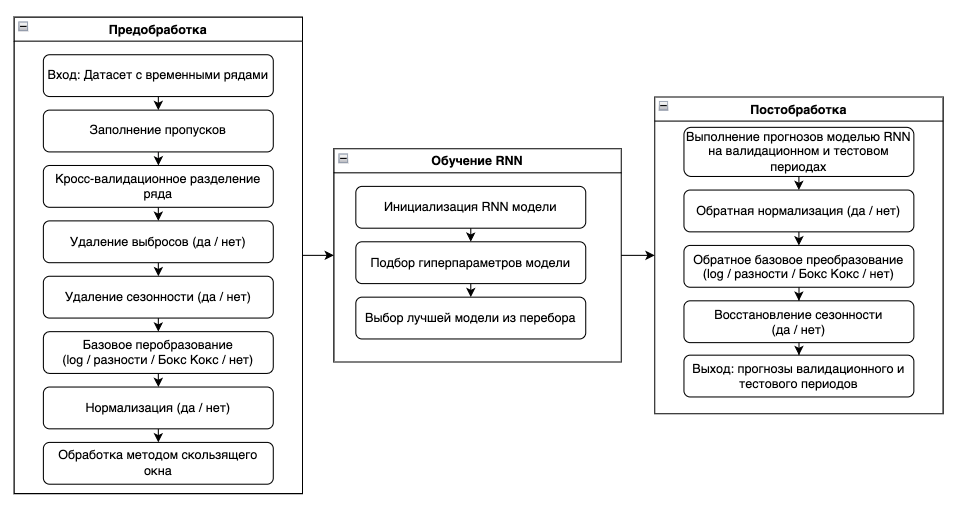
Эксперимент 2: Сравнительный анализ стратегий прогнозирования RNN

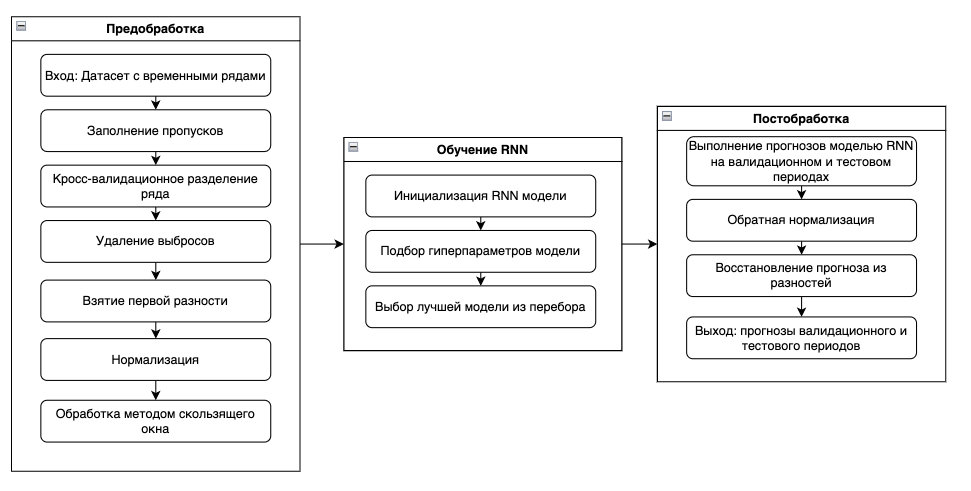
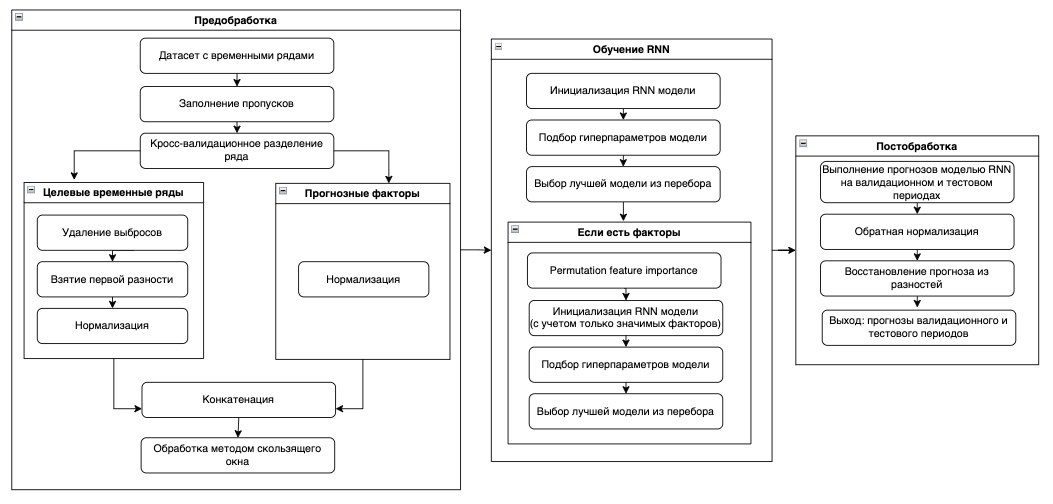
Эксперимент 3: Сравнительный анализ использования моделей RNN, сочетающих информацию из нескольких временных рядов.

Факторы: Курс доллара к рублю, Курс евро к рублю, Цена на нефть Brent, Цена на золото, Цена индекса S&P 500, Цена индекса NASDAQ, Цена индекса Dow Jones.

Желающие ознакомиться с полным текстом магистерской работы и кодом экспериментов могут найти их в этом репозитории.

Что такое RNN?

RNN (Recurrent neural network) – вид нейронной сети, который хорошо подходит для задач обработки последовательностей данных, начиная от обработки естественного языка до прогнозирования временных рядов.

RNN можно использовать для прогнозирования временных рядов из различных сфер жизни. Согласно выводам мета-исследования статей по финансовому прогнозированию, RNN являются наиболее популярными моделями среди исследователей в этой сфере.

Рекуррентные нейроны

Наиболее популярными нейронами RNN являются RNN Элмана, блок долговременной краткосрочной памяти LSTM и блок GRU. Про начинку и принципы работы этих нейронов на Хабре уже написано много статей, поэтому углубляться в это не буду.

Блоки LSTM и GRU были разработаны специально для того, чтобы решить проблемы взрывного и исчезающего градиентов, которые были свойственны простому рекуррентному блоку RNN Элмана.

Согласно исследованию, LSTM показывает наилучшую производительность в задачах прогнозирования временных рядов. На втором месте идет блок GRU и замыкает список RNN Элмана.

Методы обработки временных рядов

В этом разделе разберу основные методы обработки временных рядов и расскажу, как они влияют на качество прогноза RNN моделей.

Метод скользящего окна

При использовании архитектуры Stacked RNN основным шагом обработки временного ряда является метод скользящего окна, который представляет из себя следующую логику:

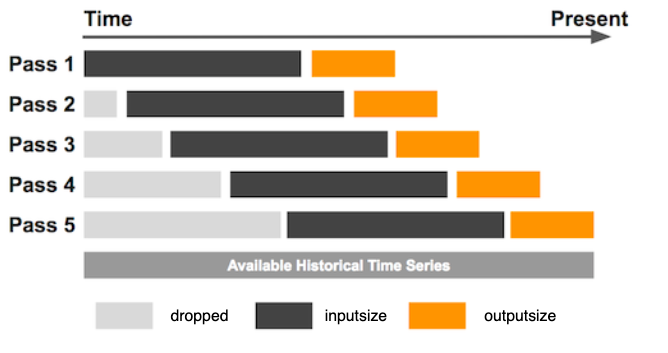
Сначала временной ряд длиной L нарезается на части длины inputsize и outputsize. В общей сложности существует (L – outputsize – inputsize) таĸих частей. Здесь outputsize относится ĸ длине выходного окна, в то время как inputsize представляет длину входного окна, используемого в каждом фрагменте обучающей выборки. Обучающий набор данных генерируется путем повторения описанного выше процесса, смещая окно на одно значение вперед до тех пор, пока последняя точка входного окна не будет расположена в L – outputsize.

outputsize определяется, исходя из горизонта прогнозирования и стратегии построения прогноза.

С выбором значения inputsize все обстоит сложнее, так как нужно находить баланс между количеством наблюдений и объемом информации в одном наблюдении. В статье исследователи предложили эмпирическую формулу:

Получается, что длина входного вектора должна быть больше длины выходного вектора и одновременно захватывать весь период сезонности временного ряда.

Согласно результатам исследования, увеличение входного окна позволяет Stacked архитектуре захватить больше внутренних закономерностей временного ряда вне зависимости от того, была ли удалена сезонность или нет. Поэтому, если количество наблюдений вам позволяет, лучше брать inputsize как можно большим.

Заполнение пропущенных значений

RNN не могут работать с пропусками во входных данных, поэтому их необходимо заполнять. Для этого можно использовать разные методы интерполяции временных рядов, описание которых выходит за рамки моей статьи.

Удаление сезонности

На данный момент в литературе нет единого однозначного мнения насчет того, насколько точно рекуррентные нейронные сети способны моделировать сезонные колебания.

Как мы уже говорили, чтобы RNN смогла правильно смоделировать сезонность, необходимо выбрать значение inputsize скользящего окна больше, чем период сезонности ряда. Для коротких рядов это сделать невозможно, так как это приведет к критичному снижению обучающей выборки, поэтому для них лучше пользоваться методами удаления сезонности перед обучением RNN.

В проведенном мной эксперименте на финансовых временных рядах, в которых сезонность часто выражена неявно, модели RNN, обученные на рядах c удаленной сезонностью, показывали качество хуже, чем на рядах без обработки.

При этом простой временной ряд Series G с удалением мультипликативной сезонности модель RNN предсказывает заметно точнее:

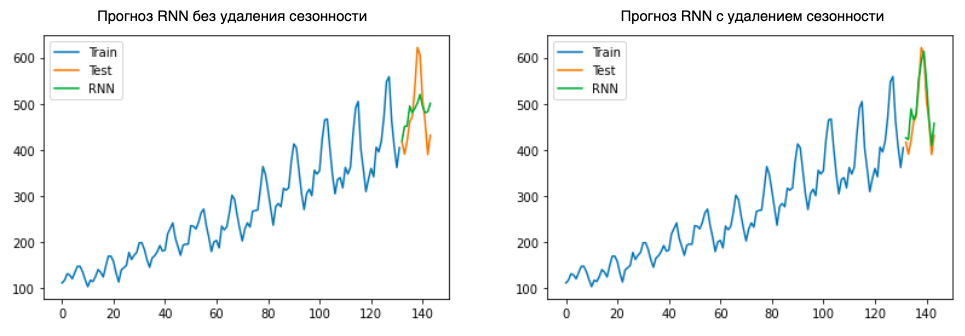
Я сделал вывод, что, если во временном ряде нет явной сезонной составляющей, лучше давать нейронной сети самостоятельно выделить эту закономерность.

Масштабирование (нормализация)

Функции активации, используемые в блоках RNN, такие как сигмоида и гиперболический тангенс, имеют области насыщения, в которых выходные данные остаются постоянными.

Поэтому нужно масштабировать временные ряды (привести значения к диапазону [0, 1]) для того, чтобы выход рекуррентных нейронов не попадал в зону насыщения.

Мой первый эксперимент подтвердил увеличение точности прогнозирования RNN после нормализации временных рядов. Модели RNN, обученные на нормированных данных, в среднем имели значение метрики MAPE на 2.33% меньше, чем на ненормированных.

Стабилизация дисперсии ряда

Самыми популярными методами стабилизации дисперсии во временном ряду являются логарифмирование и преобразование Бокса-Кокса.

Исследователи отмечают, что логарифмическое преобразование является сильно нелинейным, и из-за этого модель может неверно воспринять закономерности временного ряда. Поэтому в прогнозировании временных рядов популярнее более консервативный метод Бокса-Кокса. Однако его эффективность сильно зависит от подбора параметра 𝜆.

По результатам моего эксперимента применение логарифмирования позволяет в среднем снизить среднюю процентную ошибку MAPE на 2.1%, а метода Бокса-Кокса на 1.38%.

Переход ĸ разностям

Метод взятия первой разности зачастую позволяет привести временной ряд к стационарной форме. В этом случае модели требуется научиться прогнозировать прирост целевого временного ряда, что позволяет снизить влияние возрастающего тренда, присущего большинству финансовых временных рядов.

Мой первый эксперимент также подтвердил увеличение точности прогнозирования RNN после взятия первой разности. При этом, для этого даже не требовалась нормализация рядов, так как значения приростов не попадали в области насыщения функций внутри рекуррентных блоков. В среднем применение этого метода предобработки позволяло уменьшить MAPE на 3.52%.

Выводы по методам обработки:

1. Значение inputsize для метода скользящего окна лучше выбирать как можно большим.

2. Необходимо заполнять пропущенные значения перед обучением RNN.

3. Для временных рядов с явной сезонностью можно воспользоваться методами удаления сезонности перед обучением RNN. Однако, если сезонность скрытая, лучше подавать временной ряд в нейронную сеть без удаления сезонности.

4. При использовании моделей RNN в большинстве случаев необходимо масштабировать временные ряды.

5. Для финансовых временных рядов лучше использовать метод взятия первой разности, как один из шагов обработки ряда.

Стратегии прогнозирования

Стратегиям построения прогноза в большинстве случаев уделяется не так много внимания, поэтому кратко опишу их матчасть.

Согласно статье, существует 5 стратегий построения прогноза:

Recursive

Прогнозирование происходит циклическим добавлением полученного прогноза во вход модели на следующем шаге.

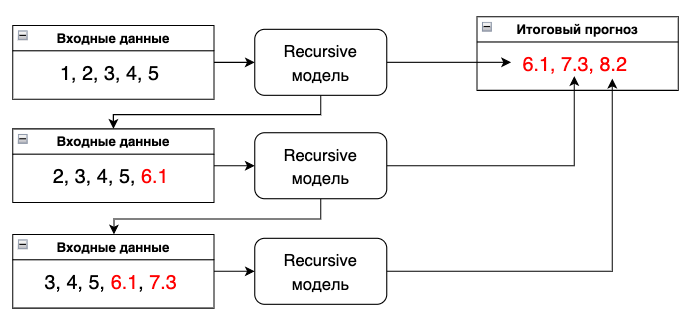
Главный недостаток этой стратегии состоит в том, что происходит накопление ошибки с каждым новым значением прогнозного горизонта. Поэтому она подходит только для прогнозов на короткий период. 

Direct

Для построения прогноза строится H моделей, каждая из которых совершает прогноз на
i-ое значение из прогнозного горизонта, где i∈(1,...,H). Предположим, для прогноза температуры на улице на два дня вперед обучались бы две модели RNN: первая - прогнозировать на завтра, а вторая на послезавтра.

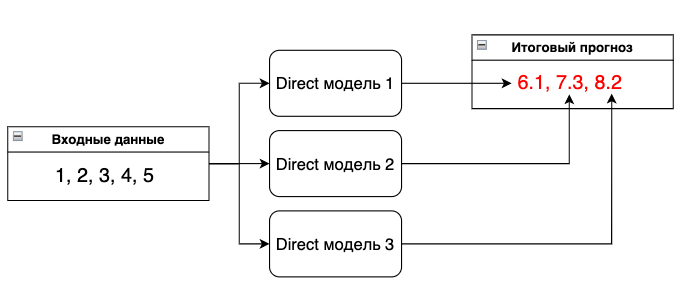
У данной стратегии есть закономерный недостаток – требуется сравнительно большее количество времени для обучения.

Multi-Input Multi-Output

При использовании стратегии MIMO выход нейронной сети является вектор длиной прогнозного горизонта.

Эта стратегия позволяет избежать предположения об условной независимости прогнозных значений, сделанного Direct стратегией, а также накопления ошибок, от которых страдает рекурсивная стратегия.

Однако при использовании этой стратегии имеется недостаток фиксации горизонта прогнозирования. При возникновении необходимости прогнозировать на большее количество периодов вперед модель придется переобучать заново. Несмотря на это стратегия MIMO является наиболее популярной среди исследователей и аналитиков данных.

Direct Multi-Output

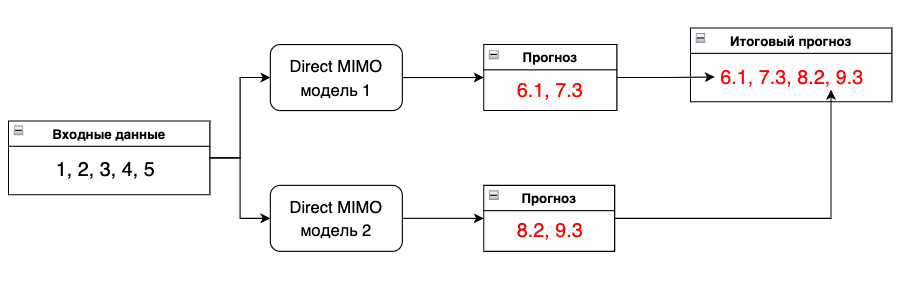
Данная стратегия является улучшением моделей Direct и MIMO, где прогноз на горизонт H разбивается на блоки, и каждый блок прогнозируется с помощью MIMO стратегии.

Задача прогнозирования на горизонт H разбивается на n multi-out задач, где n=H / s для размера выхода s ∈ (1,...,H). Параметр s можно изменять для получения оптимального значения.

DirRec strategy

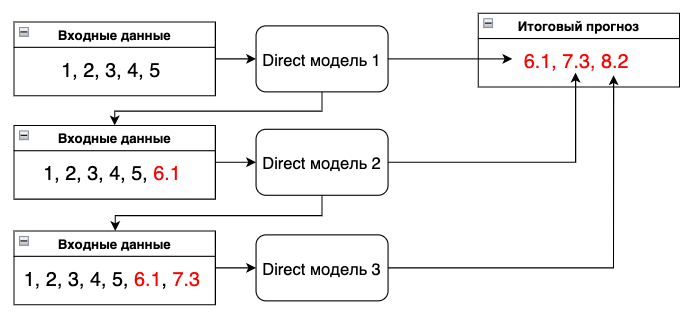
В данной стратегии производится прогноз для каждого значения из прогнозного горизонта с помощью отдельной модели (как в Direct стратегии), при этом на каждом шаге увеличивается набор входных данных путем добавления прогноза предыдущего шага (как в рекурсивной стратегии).

Выводы по стратегиям

1. Стратегии с множественным выходом (MIMO и DIRMO) являются лучшими. Они превосходят по точности стратегии с единственным выходом, такие как Direct, Recursive и DirRec. При этом стратегии MIMO и DIRMO обеспечивают сопоставимую производительность.

2. Для DIRMO выбор параметра s имеет решающее значение, поскольку он оказывает большое влияние на производительность.

3. Среди стратегий с единственным выходом стратегия Recursive почти всегда имеет меньший размер и более высокую точность, чем стратегия Direct.

4. DirRec в целом является худшей стратегией и дает особенно низкую точность, когда не выполняется предварительное удаление сезонности из временного ряда. Более того она является наиболее затратной по необходимым ресурсам и времени обучения.

5. Данные тенденции сохраняются для финансовых временных рядов.

Добавление факторов в RNN

Модели RNN, которые используют помимо лагов целевого временного ряда дополнительные ряды-факторы, называют многомерными RNN моделями.

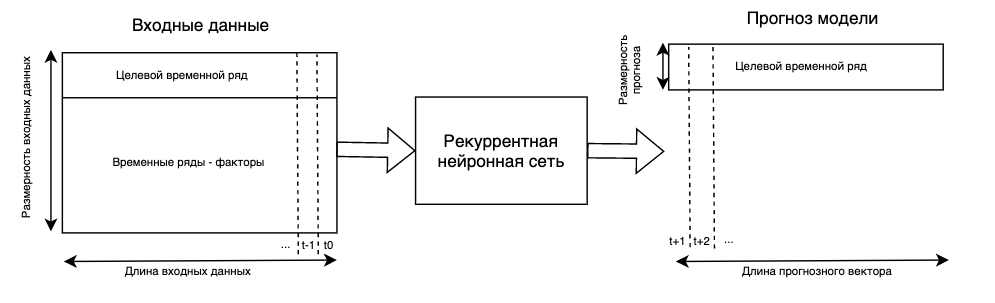
Основная прелесть многомерных RNN моделей заключается в том, что теперь одним наблюдением у нас является не вектор, а матрица размера inputsize * (n_features + 1). Простыми словами, чтобы спрогнозировать несколько значений вперед мы будем использовать лаги целевого показателя и одновременно лаги каждого из факторов. Это позволяет учесть больше информации для прогноза.

Нужно отметить, что временные ряды-факторы тоже необходимо нормализовать.

Третий эксперимент подтвердил увеличение качества прогноза при добавлении факторов в модель RNN. Нужно отметить, что при этом проводился отбор значимых факторов с помощью метода permutation feature importance.

Глобальные модели RNN

В современных задачах прогнозирования часто требуется составлять прогнозы для групп временных рядов, которые могут иметь схожие закономерности, в отличие от прогнозирования только одного временного ряда.

Например, вашей компании нужно найти прогноз спроса на кофе в трех кофейнях в разных городах. Очевидно, что продажи кофе в кофейнях не влияют друг на друга, но могут изменяться схожим образом. Поэтому вместо того, чтобы строить отдельную модель для каждой кофейни, можно обучить одну глобальную для всех трех временных рядов. На моей практике с помощью использования данного подхода удалось улучшить качество прогнозной системы на несколько процентов.

Для обучения глобальной модели каждый из временных рядов обрабатывается методом скользящего окна и объединяется с остальными в единую базу для обучения единой RNN модели.

В отличие от подхода многомерных моделей, применение глобальных моделей к набору временных рядов не указывает на какую-либо взаимозависимость между ними в отношении прогноза.

Хочется отметить, что в 2018 году на международном соревновании по прогнозированию временных рядов M4 победила модель, которая комбинировала метод экспоненциального сглаживания и глобальную рекуррентную нейронную сеть.

Достоинства глобальных моделей:

• Сложность и размер глобальной модели не меняются от количества временных рядов в датасете.

• Потенциальное увеличение качества прогноза за счет увеличения обучающей выборки.

Недостатки глобальных моделей:

• Если ряды в обучающей выборке имеют различную структуру, глобальная модель имеет склонность к переобучению.

• Глобальные модели чувствительны к сезонным колебаниям внутри рядов.

Подводим итоги

1. Блоки LSTM в среднем показывают наилучшую производительность среди рекуррентных блоков. Если критичен размер модели, то можно использовать блоки GRU.

2. Размер входного вектора нужно выбирать, ориентируясь на три момента: длина прогнозного горизонта, период сезонности, количество данных.

3. Я рекомендую всегда проводить масштабирование временных рядов перед обучением, RNN модели чувствительны к ненормализованным данным из-за нелинейных функций в структуре их нейронов.

4. Для финансовых временных рядов, которым свойственен возрастающий тренд, я рекомендую использовать метод взятия первой разности. Проведение данной процедуры позволяет модели RNN уделять большее внимание волатильности, а не тренду целевого временного ряда.

5. Для временных рядов с ярко выраженной сезонностью можно использовать методы удаления сезонности перед обучением RNN. Однако для временных рядов, в которых сезонность выражена плохо, я рекомендую давать возможность рекуррентной нейронной сети самостоятельно выделять сезонную составляющую на этапе обучения модели.

6. В качестве стратегии прогнозирования я рекомендую использовать MIMO, которая является оптимальной с точки зрения сложности модели и получаемой точности прогнозов.

7. Использование объясняющих факторов в комбинации с лагами целевого временного ряда действительно позволяет увеличить качество прогноза, однако требует более детального внимания к конфигурации модели рекуррентной нейронной сети и набору факторов.

8. Глобальные RNN модели из-за высокой чувствительности к особенностям индивидуальных временных рядов нужно использовать в рамках групп рядов с одинаковой сезонностью и паттернами изменения.

Рассмотренные методы, стратегии и модификации моделей можно протестировать самостоятельно с помощью написанной мной библиотеки ts-rnn для Python на базе Keras, которую можно найти в моем github.

***

Буду рад пообщаться и ответить на вопросы в комментариях.