Кубик Рубика и криптография: механическая шифровальная машина

Читатели на Хабре знают, что кубик Рубика — это не простая игрушка. За его разноцветными гранями скрывается целая вселенная математики. Сегодня поговорим о кубике Рубика как портативной шифровальной машине. Механика популярной головоломки основана на последовательности перестановок элементов, что делает его естественным объектом для изучения с точки зрения теории групп. В классическом кубике 3×3×3 существует более 43 квинтиллионов возможных состояний, и каждый поворот грани приводит кубик из одного состояния в другое. Именно это свойство и привлекло внимание криптографов: если кубик может генерировать такое огромное пространство перестановок, может ли он использоваться для шифрования сообщений?

Каждое состояние кубика Рубика соответствует конкретной перестановке элементов, а последовательность ходов — композиции таких перестановок. Это свойство делает его естественной моделью для криптографии, где перестановки используются для «запутывания» сообщений и создания стойких шифров.

Шифр Митчелла

Одной из первых попыток использовать кубик Рубика в криптографии стал метод, предложенный американским ученым-полиматом Дугласом Митчеллом, описанный в журнале Cryptologia в 1992 году. Митчелл предложил систему транспозиционного шифра, устойчивую к брутфорс-атакам и множественному анаграммированию, благодаря вариативности перестановок для каждого блока букв.

Инициализация кубика

В классическом методе Митчелла используется стандартный кубик Рубика 3×3×3: 6 граней по 9 квадратов, всего 54 позиции. Цвета не играют роли в шифровании, в шифре их заменяют номерами от 1 до 6. Шифр наносится поверх цветов, можно писать маркером по цветным квадратам или предварительно заклеить кубик белыми стикерами. Цвета становятся просто фоном — они не влияют на то, куда перемещаются буквы при поворотах.

Инициализация кубика начинается с того, что на одной из граней в верхнем левом углу ставится «1» – это будет передняя грань. Остальные 8 квадратов грани заполняются буквами слева направо, сверху вниз. После фиксации первой грани остается 5! (или 120) способов упорядочить оставшиеся грани. Их порядок произвольный. Каждая грань может быть ориентирована четырьмя способами (0°, 90°, 180°, 270°), что влияет на ориентацию символов на ней. Это дает более 7,25 млрд (120 × 9⁵ × 4⁵) способов начальной конфигурации размещения одного сообщения. Для еще большей сложности можно вставлять «нулевые» символы (пробелы или пустые символы - nulls) в позициях 9–48.

Для примера я взял открытый текст Митчелла.

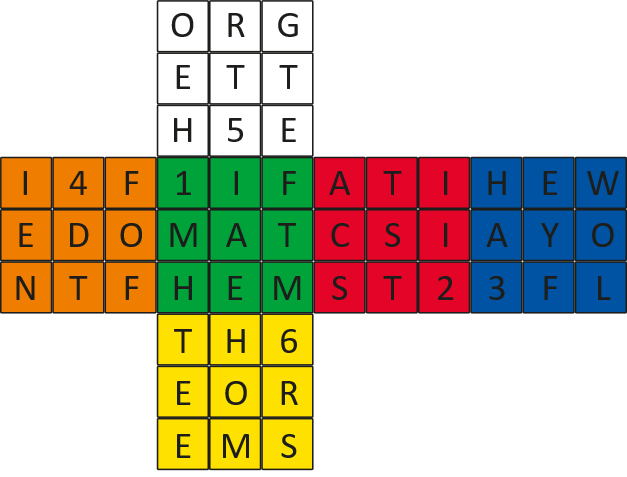
IFMATHEMATICSISTHEWAYOFLIFEDONTFORGETTHETHEOREMS

Фразу «If mathematics is the way of life, don't forget the theorems», которую можно перевести как «Если математика — это образ жизни, не забывай теоремы») я разместил на стандартной развертке кубика Рубика.  

Ключ шифрования

Ключ шифрования — это последовательность поворотов граней кубика Рубика.

Возможны 18 типов поворотов: 3 × 3 × 2:  

• 3 оси вращения: повороты рядов (rows), столбцов (columns) и уровней (levels);

• 3 возможных поворота: 90°, 180° или 270°;

• 2 варианта вращения слоев: один слой или два слоя сразу.

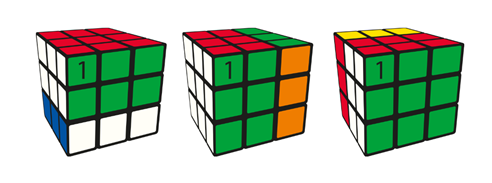
Ось поворота должна меняться на каждом шаге, чтобы избежать эквивалентных последовательностей. Кубик всегда должен быть ориентирован так, чтобы квадрат с «1» оставался в верхнем левом углу передней грани. Поэтому используется не стандартная нотация кубика (U, D, L, R, F, B с апострофами и двойками), а собственная описательная система.

Обозначения слоев по осям вращения:

• R = Row (строка);

• C = Column (столбец);

• L = Level (уровень).

Цифры после буквы: 1, 2, 3 — поворот одного внешнего слоя (single layer) по часовой стрелке; 4, 5, 6 — поворот двух внешних слоёв одновременно (double layer) по часовой стрелке:

• 1 = 90°

• 2 = 180°

• 3 = 270°

• 4 = 90°

• 5 = 180°

• 6 = 270°

Примеры:

• R3 → строка, один нижний слой, 270°

• C4 → столбец, два слоя сразу, 90°

• L6 → уровень, два слоя сразу, 270°

• R5 → строка, два слоя, 180°

Средние слои (middle layers) обычно обозначают отдельно:

• MR270 → middle row 270° (средняя строка);

• MC90 → middle column 90° (средний столбец);

• ML180 → middle level 180° (средний уровень).

Для обеспечения дополнительной «случайности» ключ шифрования может содержать информацию о том, как считывать квадраты в начале шифртекста. Можно обозначить каждую грань определённой буквой (A = верхняя грань, B = нижняя грань и так далее), чтобы расширение ключа — набор дополнительных букв в начале передаваемого ключа поворотов — подсказывало порядок считывания шифртекста. Митчелл описывает шестибуквенное расширение, например «AFDEBC» указывает принимающей стороне, что текст нужно считывать сначала с верхней грани кубика, затем с грани, обозначенной «F» …пока текст не будет скопирован на бумагу. Кроме того, Митчелл предложил обозначить порядок считывания букв дополнительной буквой в расширении ключа: предположим, X означает считывание слева направо: сначала верхняя строка, затем средняя, затем нижняя, а Y означает считывание сверху вниз, сначала левый столбец, затем центральный, затем правый».

Таким образом, ключ шифрования может выглядеть следующим образом:

ADCEBFX-R3-L2-C4-L6-R5-C1-R3-L4-R1, где

• ADCEBFX - расширение ключа (key extension), 7 символов, которые определяют порядок считывания граней при шифровании/дешифровке (6 букв A–F) и дополнительный индикатор направления чтения (X или Y).

• R3-L2-C4-L6-R5-C1-R3-L4-R1 последовательность поворотов из 10 ходов (rotation key).

На практике это работает следующим образом:

• Отправитель пишет открытый текст на кубик (по номерам 1–6).

• Держит кубик с «1» в верхнем левом углу передней грани.

• Выполняет эти 10 поворотов по порядку.

• Затем считывает буквы по порядку граней A → D → C → E → B → F (не 1–6!), в направлении X (строки слева направо).

• Получается шифртекст — и отправляет его получателю.

• Получатель наносит шифртекст обратно на кубик в том же порядке (A D C E B F, X).

• Выполняет эти же повороты в обратном порядке и с инверсией направления (R3 → R1 вместо R3, потому что 270° против = 90° по часовой, и т.д.).

• Получает исходный текст.

Взлом шифра

Митчелл утверждал, что система устойчива, поскольку каждый блок из 48 букв можно инициализировать по-разному (разные порядки граней, разные ориентации, разные nulls), что дает более 7 миллиардов возможных инициализаций; количество возможных ключей поворотов (при k=30 ходов) — около 2,3 × 10³⁵, а также 48! (≈ 1,2 × 10⁶¹) возможных транспозиций для каждого блока — по его мнению, делают полный перебор невозможным.

Однако критики метода показали, что Митчелл сильно переоценил безопасность. Во-первых, он не учел ограничения группы кубика (из 48! возможных перестановок достижимы только ~4,3 × 10¹⁹ состояний). Во-вторых, в 2010 году было доказано, что любое состояние кубика достижимо максимум за 20 ходов (God's number = 20), а медианное значение — 18 ходов. В-третьих, повторяющиеся буквы сильно сужают эффективное пространство ключей. В английском алфавите всего 26 букв, и в сообщениях из 48 символов очень много повторений (E, T, A, O, I, N и т.д.) — компьютер может использовать статистику языка (частоты букв, биграммы, квадграммы), чтобы быстро отсеивать бессмысленные варианты. И, наконец, Митчелл не учел принцип Керкхоффса, когда система остается безопасной, даже если противник знает всё о системе, кроме секретного ключа.

Последнее наглядно доказал крипто-челлендж Клауса Шмеха, известного немецкого эксперта по криптографии. В 2018 году в своем блоге Cipherbrain Шмех описал метод Митчелла и предложил своим читателям расшифровать 48-символьное послание, зашифрованное кубиком Рубика:

1GDWOHOER GTNTTROI3 AET2NEV5N EIOYR6IBO WEHM4UCOD TNEIEMYET

Через несколько месяцев астроном из Тюбингенского университета Кристоф Тензер ответил Клаусу: «Встретимся завтра вечером в городе на деревянном мосту».

MEET YOU AT THE WOODEN BRIDGE IN THE CITY TOMORROW EVENING

Это был исходный текст, который Кристоф расшифровал. Он изучил метод Митчелла. Сначала он пробовал алгоритм подъёма на холм (hill climber), чтобы собрать кубик «с нуля» – не сработало по причине слишком короткого текста и повторов букв, из-за чего слишком много вариантов сборки выглядели «почти осмысленно», и hill climber не мог выбрать правильный. Перешел к брутфорс и с готовой библиотекой на Python для моделирования ходов кубика перебирал все комбинации ходов глубиной до 6–7. Процесс шел слишком медленно — не хватало мощности. Написал свою быструю реализацию всех ходов кубика, перенес программу на C++ для скорости, перебирал все комбинации ходов глубиной до 12. Для проверки каждого состояния считывал буквы по граням в порядке 1–6, оценивал по квадграммам английского языка на гранях — чем выше балл, тем текст вероятнее осмысленный. Поскольку номеров 1–6 должно быть ровно по одному на каждой грани (иначе состояние неверное), почти все комбинации отсеивались сразу без проверки квадграмм, что сильно ускорило процесс. Использовал дополнительные оптимизации: пропускал ходы, которые отменяют предыдущие (например, MC90 → MC90 → MC90 эквивалентно MC270); учитывал, что многие пути ведут к одному и тому же состоянию — не проверял дубликаты.

Программа проверяла ≈4 500 000 ключей (комбинаций ходов) в секунду и работала около двух недель на обычном домашнем ПК. В итоге программа нашла частично читаемое состояние (не полностью собранный кубик, но текст уже узнавался). Позже Кристоф отметил: даже если настоящий ключ — 20 ходов, программа найдёт гораздо более короткий эквивалентный путь (≤12 ходов), и это все равно будет работать.

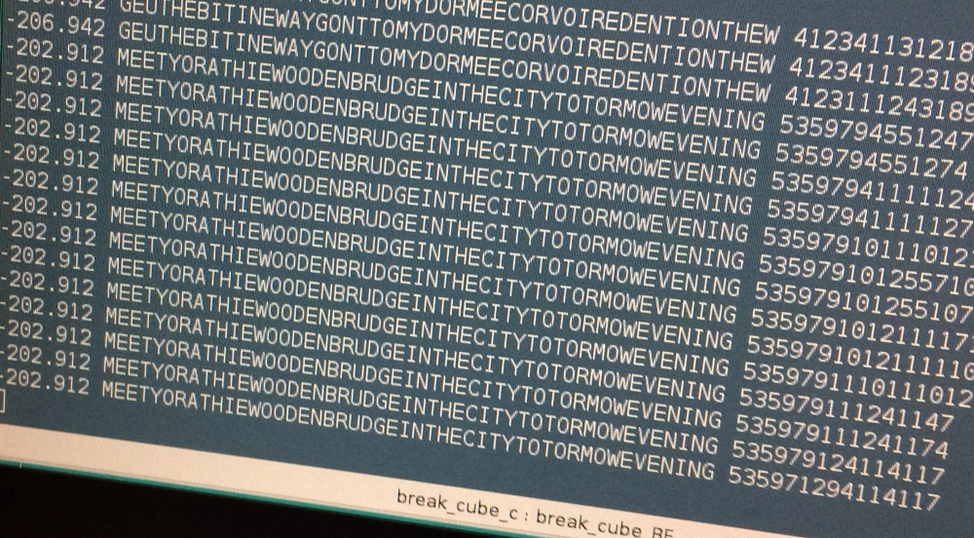
На скриншоте программы, который Кристоф прислал Клаусу, число слева — это quadgram score (чем выше — тем лучше), далее — вариант исходного сообщения, затем последовательность ходов (цифры 5, 3, 5… — это коды поворотов в его нотации, например 5 = 180° double layer и т.д.).

Пример шифрования Митчелла (1992) очень хорош как учебный пример, который показывает красоту и слабости транспозиционных шифров, важность принципа Керкхоффса и обманчивость огромного пространства ключей. Кроме того, этот метод имеет интересный гибридный аспект, поскольку сочетает реальный кубик Рубика и компьютерную систему (или хотя бы потенциал для автоматизации). Это пример шифра, который живёт в двух мирах одновременно: физическом (ручное кручение кубика оффлайн) и цифровом (моделирование в программе — быстро и масштабируемо), и позволяет переходить от одного к другому без потери смысла. Это своеобразный мост между руками и кодом. Но все же как надежный шифр для реального использования и защиты сообщений он не годится.

Кубик Рубика в современных методах шифрования

Если шифр Митчелла 1992 года — это классическая транспозиция, то современная теория уходит гораздо глубже. В работе 2011–2013 годов Rubik’s for Cryptographers (Кубик Рубика для криптографов) Кристоф Пети и Жан-Жак Кискатер показывают, что математические задачи, связанные с кубиком Рубика (в первую очередь, в неабелевых группах), имеют прямые аналогии с задачами, на которых строится безопасность некоторых криптосистем, в первую очередь, с хеш-функциями Кэли — классом криптографических хеш-функций, основанных на графах Кэли и умножении в неабелевых группах.

Главный вывод, к которому приходят бельгийские криптографы: хотя простые перестановки кубика не дают защищенного алгоритма, его абстрактные обобщения в рамках теории групп могут служить источником криптографически сложных задач.

Кубик Рубика как иллюстрация некоммутативных групп также интересен и в контексте постквантовой криптографии — раздела, изучающего алгоритмы, устойчивые к квантовым компьютерам. Поскольку последовательность ходов — это набор элементов группы, где порядок важен, возникает аналогия с созданием криптосхем, безопасность которых основана на трудности решения определённых задач в некоммутативных группах (аналогично задачам сборки кубика, но в более сложных структурах).

Кубик Рубика вдохновил разработчиков ряда современных крипто-подходов, особенно в шифровании изображений:

• Гибридные алгоритмы с хаосом: Кубик Рубика комбинируется с гиперхаотическими системами (Lorenz, logistic mapping, 7D/8D хаос), параллельными ротациями и диффузией (скрамблинг с перестановкой битов по слоям, поворотом кадров и круговыми сдвигами. Такие схемы достигают высоких значений NPCR (>99.6%), UACI (33.5%) и энтропии (7.99), устойчивы к дифференциальным и plaintext-атакам.

• Квантово-вдохновленные и оптические методы, когда авторы берут идеи из квантовой физики (quantum walks), оптики (хаос света) и биологии (ДНК-кодирование) и комбинируют их с принципом кубика Рубика.

• Продвинутые способы «перемешивания» пикселей изображения, чтобы шифртекст выглядел как полный хаос: с применением Lucas Q-matrix, шифрованием нескольких изображений одновременно, используя покерную логику.

• Гибридные транспозиции: улучшение классического шифра через интеграцию в него принципов кубика Рубика.

Эти подходы не обязательно используют физический кубик Рубика, но принципы его перестановок лежат в основе алгоритмов, которые активно публикуются в журналах вроде Optik, Entropy, Scientific Reports и применяются для защиты мультимедиа контента.

Дешифровка…

Кубик Рубика в очередной раз обнаруживает новую грань — теперь криптографию:

• он выступает наглядной моделью перестановок, что важно для криптографии;

• он может использоваться для создания ручных шифров, в первую очередь, для обучения и развлечения;

• он стал предметом крипто-челленджа, который доказал уязвимость простых шифровальных схем, и напомнил, что большое пространство состояний — не то же самое, что криптоустойчивость.

• и наконец, он стал источником математических идей для современных криптографических концепций, включая постквантовые направления и продвинутые алгоритмы шифрования изображений.

Крутите кубик Рубика — и пусть у вас всё сложится!