Рубрика «занимательная математика»
Теорема Пифагора: великий обман школьной программы. Как абстракция убила смысл
2025-12-02 в 2:26, admin, рубрики: векторная алгебра, геометрия, доказательство, занимательная математика, линейная алгебра, математика, образование, симметрия, теорема Пифагора, школьная программаВсе мы знаем эту формулу .
Это, пожалуй, единственное знание из школьной геометрии, которое остается с человеком на всю жизнь, даже если он работает баристой или курьером.
Но задавали ли вы себе когда-нибудь вопрос: почему именно квадраты?
Читать полностью »
Зеркальные равенства: красивая математическая симметрия
2025-08-26 в 8:20, admin, рубрики: python, алгоритм, занимательная математика, зеркальные равенства, код, палиндром
Математика полна удивительных закономерностей. В одном из номеров журнала «Наука и жизнь» была небольшая заметка в разделе «Математические досуги». С двумя примерами на умножение из разряда математических неожиданностей.
Как с помощью циркуля и линейки находить корни, квадраты и обратные величины чисел
2021-05-07 в 16:40, admin, рубрики: Алгоритмы, занимательная математика, Занимательные задачки, логические игры, математика, ЦиркульПредставьте, что у вас нет под рукой калькулятора (но есть циркуль и линейка или угольник) и вам нужно посчитать результат в виде отрезка. Задача решается за менее чем 5 простых шагов.
Базовая формула вычисления
Для начала докажем одну формулу, которая нам будет помогать с дальнейшим решением.
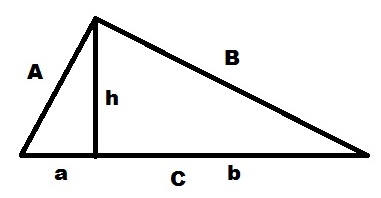
В прямоугольном треугольнике ABCЧитать полностью »
Занимательная математика. Самая экономичная система счисления
2018-10-28 в 1:50, admin, рубрики: занимательная математика, математика, системы счисления, ЭпсилонВсе мы знаем из школьного курса что такое системы счисления(СС). Но не все задумываются о том, на сколько затратны СС. Т.е. какой набор цифр нам необходим для представления числа в данной СС. Когда у нас есть ограниченный набор уникальных элементов (разноцветные камушки разных размеров), с помощью которого мы можем представить число, какое максимальное число мы можем представить используя эти элементы? (все красные камушки — это ноль, зелёные — один, синие — два и т.д., маленькие — нулевой разряд, средние — первый, большие — второй и т.д.). Где та грань, при которой основание СС играет большую роль чем разрядность числа?
Читать полностью »
Теория счастья. Термодинамика классового неравенства
2018-10-14 в 10:39, admin, рубрики: recreational science, занимательная математика, Занимательные задачки, кривая Лоренца, математика, Научно-популярное, теория вероятности и мат статистика, теория счастья, термодинамика, экономическая модель, энтропияПродолжаю знакомить читателей Хабра с главами из своей книжки «Теория счастья» с подзаголовком «Математические основы законов подлости». Это ещё не изданная научно-популярная книжка, очень неформально рассказывающая о том, как математика позволяет с новой степенью осознанности взглянуть на мир и жизнь людей. Она для тех кому интересна наука и для тех, кому интересна жизнь. А поскольку жизнь наша сложна и, по большому счёту, непредсказуема, упор в книжке делается, в основном, на теорию вероятностей и математическую статистику. Здесь не доказываются теоремы и не даются основы науки, это ни в коем случае не учебник, а то, что называется recreational science. Но именно такой почти игровой подход позволяет развить интуицию, скрасить яркими примерами лекции для студентов и, наконец, объяснить нематематикам и нашим детям, что же такого интересного мы нашли в своей сухой науке.
Опубликованные главы:
• Введение в мерфологию
• Закон арбузной корки и нормальность ненормальности
• Закон зебры и чужой очереди
• Проклятие режиссёра и проклятые принтеры
В этой главе мы порассуждаем о деньгах, рынках и энтропии, а также посмотрим на анимированные гифки, которых, увы, в книжке напечатать не получится.

Теория счастья. Проклятие режиссёра и проклятые принтеры
2018-09-07 в 9:27, admin, рубрики: recreational science, дедлайн, занимательная математика, Занимательные задачки, кривая Лоренца, математика, Научно-популярное, пуассоновский процесс, распределение пуассона, теория вероятности и мат статистика, теория счастья, числа СтирлингаПродолжаю знакомить читателей Хабра с главами из своей книжки «Теория счастья» с подзаголовком «Математические основы законов подлости». Это ещё не изданная научно-популярная книжка, очень неформально рассказывающая о том, как математика позволяет с новой степенью осознанности взглянуть на мир и жизнь людей. Она для тех кому интересна наука и для тех, кому интересна жизнь. А поскольку жизнь наша сложна и, по большому счёту, непредсказуема, упор в книжке делается, в основном, на теорию вероятностей и математическую статистику. Здесь не доказываются теоремы и не даются основы науки, это ни в коем случае не учебник, а то, что называется recreational science. Но именно такой почти игровой подход позволяет развить интуицию, скрасить яркими примерами лекции для студентов и, наконец, объяснить нематематикам и нашим детям, что же такого интересного мы нашли в своей сухой науке.
Опубликованные главы:
• Введение в мерфологию
• Закон арбузной корки и нормальность ненормальности
• Закон зебры и чужой очереди

Мы порассуждаем о цейтнотах, дедлайнах и о невовремя ломающихся принтерах.
Теория счастья. Закон зебры и чужой очереди
2018-08-19 в 4:08, admin, рубрики: recreational science, занимательная математика, Занимательные задачки, кривая Лоренца, математика, Научно-популярное, пуассоновский процесс, случайное блуждание, теория вероятности и мат статистика, теория счастья, цепи марковаПродолжаю знакомить читателей Хабра с главами из своей книжки «Теория счастья» с подзаголовком «Математические основы законов подлости». Это ещё не изданная научно-популярная книжка, очень неформально рассказывающая о том, как математика позволяет с новой степенью осознанности взглянуть на мир и жизнь людей. Она для тех кому интересна наука и для тех, кому интересна жизнь. А поскольку жизнь наша сложна и, по большому счёту, непредсказуема, упор в книжке делается, в основном, на теорию вероятностей и математическую статистику. Здесь не доказываются теоремы и не даются основы науки, это ни в коем случае не учебник, а то, что называется recreational science. Но именно такой почти игровой подход позволяет развить интуицию, скрасить яркими примерами лекции для студентов и, наконец, объяснить нематематикам и нашим детям, что же такого интересного мы нашли в своей сухой науке.
Опубликованные главы:
• Введение в мерфологию
• Закон арбузной корки и нормальность ненормальности

Мы поговорим о фатуме, землетрясениях, очередях и замечательных процессах: пуассоновском потоке, случайном блуждании и немного о цепях Маркова.
Теория счастья. Введение в мерфологию
2018-07-20 в 18:57, admin, рубрики: recreational science, занимательная математика, индекс Джини, кривая Лоренца, математика, Научно-популярное, парадокс инспекции, принцип Парето, теория вероятности и мат статистика, теория счастьяПродолжаю знакомить читателей Хабра с главами из своей книжки «Теория счастья» с подзаголовком «Математические основы законов подлости». Это ещё не изданная научно-популярная книжка, очень неформально рассказывающая о том, как математика позволяет с новой степенью осознанности взглянуть на мир и жизнь людей. Она для тех кому интересна наука и для тех, кому интересна жизнь. А поскольку жизнь наша сложна и, по большому счёту, непредсказуема, упор в книжке делается, в основном, на теорию вероятностей и математическую статистику. Здесь не доказываются теоремы и не даются основы науки, это ни в коем случае не учебник, а то, что называется recreational science. Но именно такой почти игровой подход позволяет развить интуицию, скрасить яркими примерами лекции для студентов и, наконец, объяснить нематематикам и нашим детям, что же такого интересного мы нашли в своей сухой науке.
Опубликованные главы:
Это, одна из первых глав, в которой на примере велосипедиста рассматриваются нужные нам инструменты для измерения несправедливости: кривая Лоренца и индекс Джини, а также упоминаются пресловутый Парето и грозный инспектор.

Теория счастья. Закон арбузной корки и нормальность ненормальности
2018-07-10 в 4:28, admin, рубрики: recreational science, занимательная математика, Занимательные задачки, математика, Научно-популярное, теория вероятности и мат статистика, теория счастьяПредставляю на суд читателей Хабра неупорядоченные главы из своей книжки «Теория счастья» с подзаголовком «Математические основы законов подлости». Это ещё не изданная научно-популярная книжка, очень неформально рассказывающая о том, как математика позволяет с новой степенью осознанности взглянуть на мир и жизнь людей. Она для тех кому интересна наука и для тех, кому интересна жизнь. А поскольку жизнь наша сложна и, по большому счёту, непредсказуема, упор в книжке делается, в основном, на теорию вероятностей и математическую статистику. Здесь не доказываются теоремы и не даются основы науки, это ни в коем случае не учебник, а то, что называется recreational science. Но именно такой почти игровой подход позволяет развить интуицию, скрасить яркими примерами лекции для студентов и, наконец, объяснить нематематикам и нашим детям, что же такого интересного мы нашли в своей сухой науке.
В этой главе мы начнём с анализа арбузов и их корок, выясним их связь со знаменитым законом Мерфи и убедимся со всей строгостью в том, что о вкусах не спорят.

