Рубрика «симметрия»
MDSI Solver: программная реализация метода создания двусторонних мозаик из кубиков Рубика
2026-01-12 в 6:00, admin, рубрики: двусторонняя мозаика, дизайн, кубик рубика, мозаика из кубиков рубика, рубиккубизм, симметрияВ статье я рассказываю о программной реализации своего MDSI-метода (Mirror Dual-Sided Inverse), разработанного для сборки зеркальных двусторонних инверсивных паттернов на кубике Рубика. Программа MDSI Solver объединяет MDSI-метод и двухфазный алгоритм Герберта Коцембы (kociemba two-phase algorithm). MDSI-метод находит полное состояние кубика на основе двух заданных противоположных граней, а затем алгоритм Коцембы генерирует оптимальное или близкое к оптимальному решение, обычно составляющее 20 или меньше ходов для сборки паттерна.
Еще раз о симметрии кубика Рубика. «Зеркало» двусторонних MDSI-паттернов
2026-01-08 в 7:20, admin, рубрики: головоломки, двусторонняя мозаика, дизайн, занимательные задачи, кубик рубика, логика, мозаика из кубиков рубика, рубиккубизм, симметрия, теория группЭто статья является дополнением к большому материалу Симметрия кубика Рубика, где я рассказывал о своем методе сборки зеркальных двусторонних инверсивных паттернов Mirror Dual-Sided Inverse (MDSI) на кубике Рубика. Я посчитал нужным дополнительно объяснить, как эвристически искал доказательство того, что возможно на противоположных сторонах кубика Рубика собрать любой (2-, 3-, 4-, 5- и 6-цветный) MDSI паттерн. Для этого я ввел понятие «зеркало» для среднего слоя, который отражает противоположные стороны и применил правило четности пермутаций.
***
Теория групп для всех: пульт для управления реальностью прямо из палаты
2025-12-23 в 11:51, admin, рубрики: визуализация, математика, перестановки, симметрия, теория группПочему теория групп порой кажется сложной и непонятной
Представьте себе, что вы открываете учебник по математике. На первой же странице видите:
«Гру́ппа — множество, на котором определена ассоциативная бинарная операция, причём »
В этот момент у вас сразу же появляются вопросы:
-
Откуда взялось это множество и зачем оно нужно?
-
Какая операция и что это вообще всё значит?
-
Почему я должен верить в эти аксиомы?
Теорема Пифагора: великий обман школьной программы. Как абстракция убила смысл
2025-12-02 в 2:26, admin, рубрики: векторная алгебра, геометрия, доказательство, занимательная математика, линейная алгебра, математика, образование, симметрия, теорема Пифагора, школьная программаВсе мы знаем эту формулу .
Это, пожалуй, единственное знание из школьной геометрии, которое остается с человеком на всю жизнь, даже если он работает баристой или курьером.
Но задавали ли вы себе когда-нибудь вопрос: почему именно квадраты?
Читать полностью »
Симметрия простых чисел
2025-11-07 в 9:08, admin, рубрики: гипотеза Гольтбаха, математика, поиск больших простых чисел, простые близнецы, простые числа, симметрияРассмотрим структуру простых чисел, их симметрию и введем новые определения. Применяя симметрию рассмотрим способ поиска простых чисел, задачу бесконечности близнецов и гипотезу Гольтбаха.
1. Симметрия простых чисел
Как известно, простые числа делятся без остатка только на себя и 1. Визуально это можно представить решетом Эратосфена. Давайте посмотрим наглядно, но используем не одну линию, а таблицу, где каждый делитель будет на своем слое.
Почему физики и программисты мыслят одинаково: законы симметрии кода и Вселенной
2025-10-28 в 13:40, admin, рубрики: Алгоритмы, вычисления, инвариантность, код, логика, мышление программиста, наука, симметрия, физика, энтропияИногда кажется, что физика и программирование живут в разных мирах. Но чем глубже смотришь, тем сильнее понимаешь — законы мышления, которыми мы руководствуемся, удивительно схожи. Симметрия, порядок, борьба с энтропией, поиск инвариантов — всё это объединяет инженеров, физиков и программистов в одном стремлении понять, как устроен мир. Я просто захотел порассуждать об этом и поделиться с вами своими мыслями.
Рекурсивная Гипотеза Реальности – от аксиомы к сильному ИИ. Статья 1
2025-03-24 в 17:55, admin, рубрики: алгоритм, дуализм, мультивселенная, рекурсия, симметрия, случайность, сознание
Что, если реальность — это алгоритм, который пишет сам себя?
Как теорема Нётер произвела революцию в физике
2025-02-14 в 13:49, admin, рубрики: симметрия, теорема нётерЭмми Нётер показала, что фундаментальные физические законы являются следствием простых симметрий. Спустя столетие её открытия продолжают формировать физику.
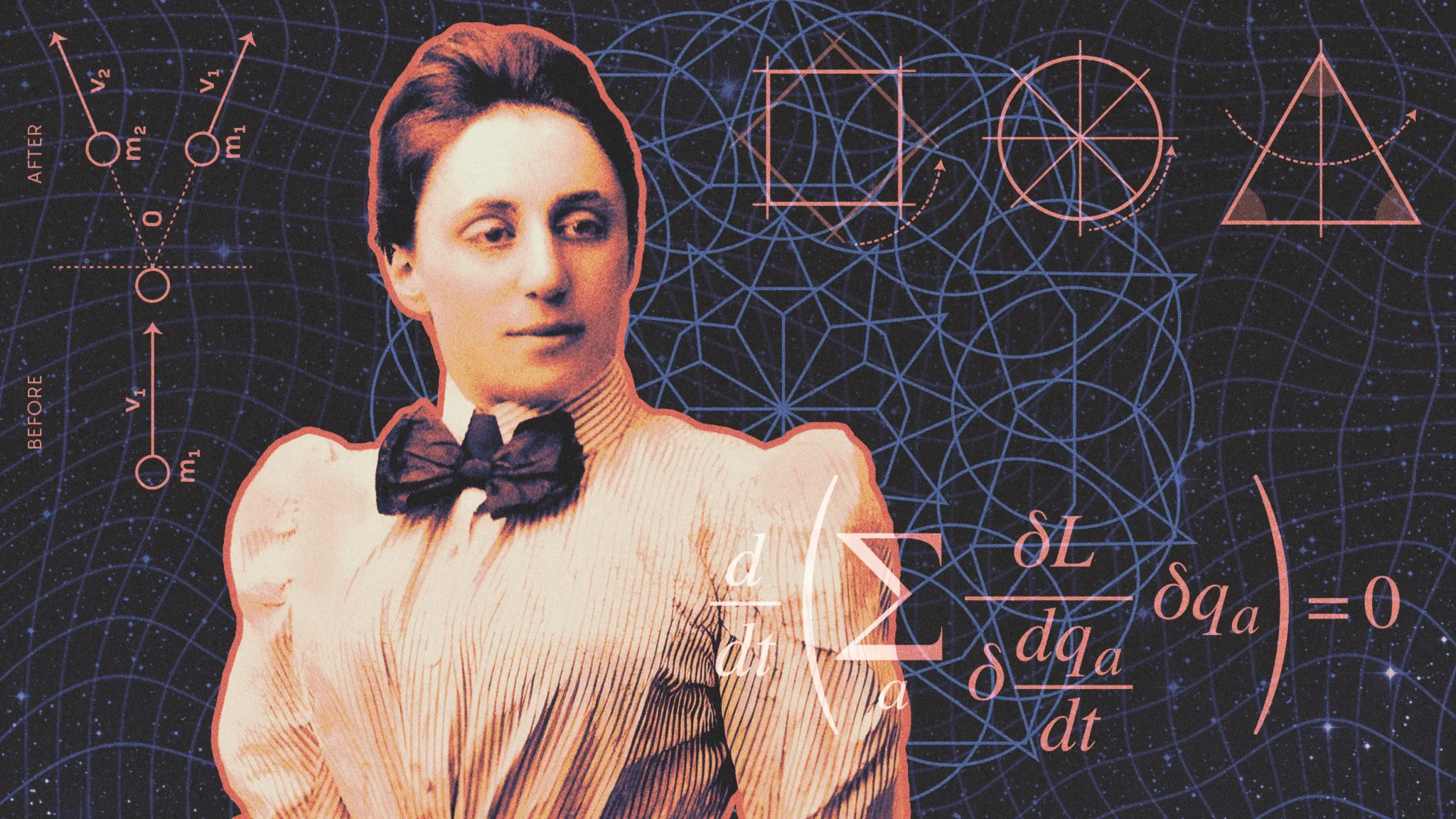
Осенью 1915 года фундамент физики начал давать трещину. Новая теория гравитации Эйнштейна, казалось, подразумевала возможность создания и уничтожения энергии, что грозило перевернуть двухвековые представления о физике.
