Продолжаю знакомить читателей Хабра с главами из своей книжки «Теория счастья» с подзаголовком «Математические основы законов подлости». Это ещё не изданная научно-популярная книжка, очень неформально рассказывающая о том, как математика позволяет с новой степенью осознанности взглянуть на мир и жизнь людей. Она для тех кому интересна наука и для тех, кому интересна жизнь. А поскольку жизнь наша сложна и, по большому счёту, непредсказуема, упор в книжке делается, в основном, на теорию вероятностей и математическую статистику. Здесь не доказываются теоремы и не даются основы науки, это ни в коем случае не учебник, а то, что называется recreational science. Но именно такой почти игровой подход позволяет развить интуицию, скрасить яркими примерами лекции для студентов и, наконец, объяснить нематематикам и нашим детям, что же такого интересного мы нашли в своей сухой науке.
Опубликованные главы:
• Введение в мерфологию
• Закон арбузной корки и нормальность ненормальности
Мы поговорим о фатуме, землетрясениях, очередях и замечательных процессах: пуассоновском потоке, случайном блуждании и немного о цепях Маркова.
Закон зебры
Говорят, что жизнь похожа на зебру: то белая полоса, то чёрная… А ещё бывает, что к одной неприятности добавляется другая, и так непросто в жизни а тут ещё кошка рожать принялась! То густо, то пусто! Одно одному! Но самое печальное, что когда хорошо и в жизни настала светлая полоса, мысли закрадываются нехорошие: ох, не сглазить бы, ох, не придётся ли за счастье расплачиваться… Знакомое ощущение? По этому поводу сформулирован один из законов мерфологии — второй закон Чизхолма: "Когда дела идут хорошо, что-то должно случиться в самом ближайшем будущем". Но так как Френсис Чизхолм, в своей оригинальной работе не даёт детального анализа или доказательства этого закона, мы постараемся сами выяснить кроется ли за этим какая-либо закономерность, или нам так только кажется. А если это причуды математики, то можно ли определить характерную длительность или частоту полосок на теле нашей зебры, и от чего она зависит?
В жизни то и дело происходят события. Иногда они вовсе не связаны друг с другом, иногда образуют цепочки причинно-следственных связей. Рассуждения об этих связях, цепочках и предопределённости жизненного пути могут увести нас очень далеко, и мы поговорим о них позже. А пока давайте попробуем, как всегда, обойтись наименьшим количеством исходных данных для анализа нашего закона. Рассмотрим последовательность никак не связанных между собой событий, и посмотрим, что удастся из неё добыть.
События, которые никак не связаны между собой и происходят во времени случайным образом описываются с помощью хорошо известного пуассоновского потока. Он соответствует многим случайным явлениям от землетрясений до появления покупателей в магазине. Пуассоновский поток событий характеризуется интенсивностью или плотностью потока — параметром, который определяет ожидаемое число событий в единицу времени. Например, при измерении времени в днях, значению параметра 
будет соответствовать цепочка случайных событий, в среднем, случающихся раз в неделю. Это вовсе не означает, что события будут происходить с частотой раз в неделю. Никакой выделенной частоты у последовательности событий может и не быть вовсе. Лучше всего представлять себе пуассоновский поток с интенсивностью раз в неделю так: в году 52 недели, значит, в год должно произойти около 52 событий (в среднем, за много лет). Если мы выберем 52 случайных равномерно распределённых даты в году, то их можно рассматривать, как моменты возникновения абсолютно независимых пуассоновских событий.
Пример построения пуассоновского потока с интенсивностью 1/7 (время измеряется в днях). На отрезке в 365 дней случайным образом разбросали никак не связанные между собой 52 события.
При этом о какой-либо периодичности в этих событиях речь не идёт, когда пожелают, тогда и случатся. Но и в этом беспорядке статистика может нам показать определённые закономерности. Например, распределение длительности периодов между событиями, показанными на предыдущем рисунке, будет вовсе не равномерным.
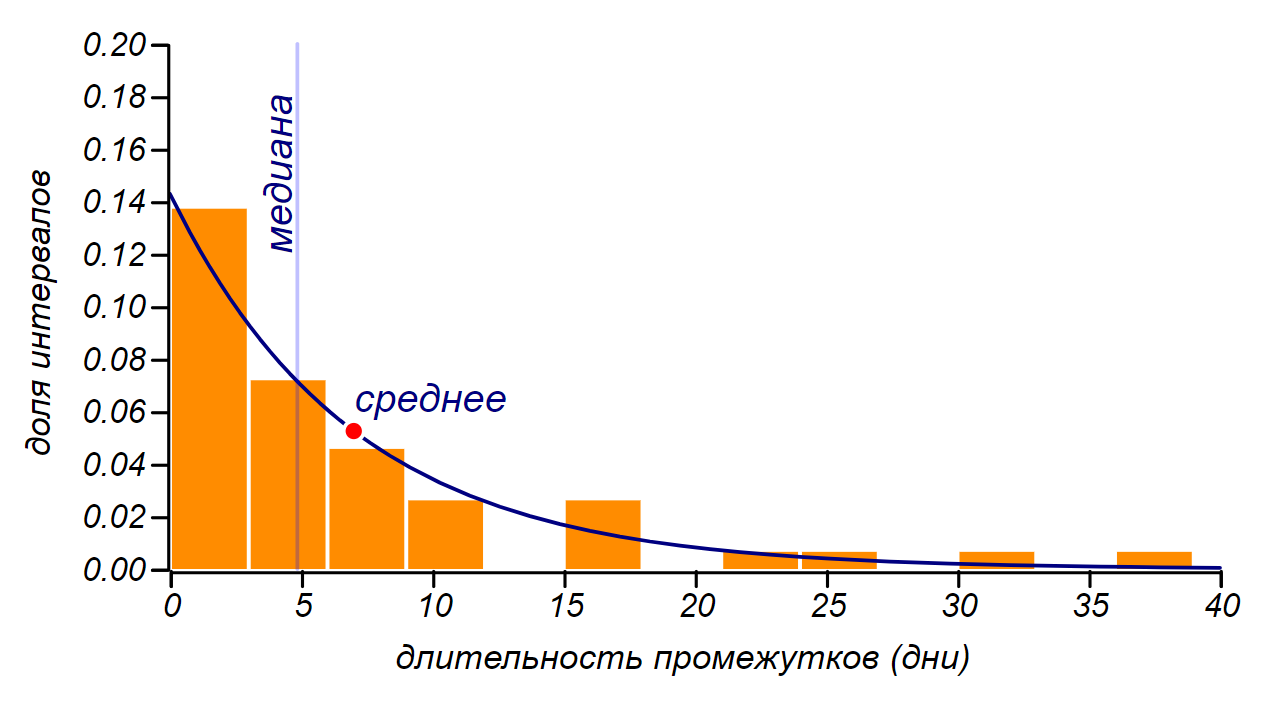
Плотность распределения длительностей промежутков между 52 событиями, случайно разбросанными по отрезку в 365 дней.
Распределение длительностей промежутков стремится к экспоненциальному, оно показано сплошной линией. У этого распределения максимум (мода) находится в нуле, а среднее значение, равно как раз 7 дням. Более того, стандартное отклонение тоже будет равно 7 дням. Равенство стандартного отклонения и среднего значения — характерное свойство экспоненциального распределения. Как видите, эти характеристики вовсе не гарантируют того, что между событиями будет проходить одна неделя, в среднем — да, но чаще всего — меньше, к тому же, могут наблюдаться и достаточно долгие промежутки. Наконец, медиана показывает, что половина всех промежутков будет иметь длительность не превышающую 5 дней. Интенсивность и частота совсем не одно и тоже, это очень важное замечание!
Для справедливости, положим, что хорошие и плохие события происходят равновероятно, но яркие и значимые события случаются существенно реже мелких и незначительных. Пусть это будет нормальная жизнь, в которой эмоциональная окраска событий подчиняется нормальному (гауссовому) распределению. Вот как может выглядеть год синтетической судьбы, как череды случайных абсолютно независимых жизненных перипетий:
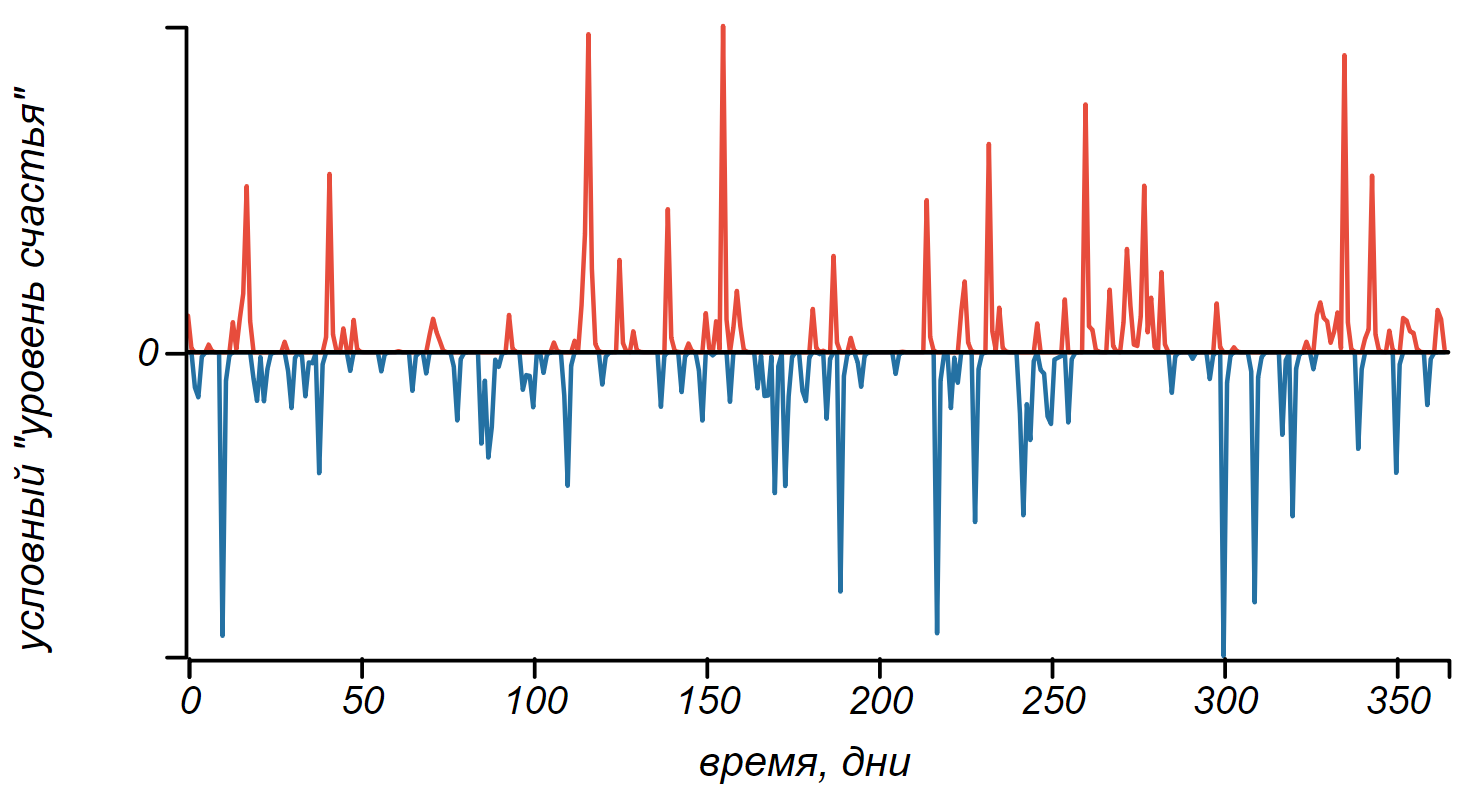
Череда событий различной эмоциональной окраски, образующая пуассоновский поток с интенсивностью 2/7 (2 события в 7 дней).
Пока никаких полос не наблюдается, вместо этого есть некий шум. Каждое событие проходит бесследно, ничего не оставляя ни в памяти, ни в настроении. Так не бывает, давайте наделим нашего модельного героя памятью, для начала, идеальной. Каждое событие пусть навсегда врежется ему в память и в настроение, соответственно, либо улучшая, либо ухудшая его. Вот какую картинку мы можем получить, пронаблюдав за судьбой нашего героя на протяжении десяти лет.
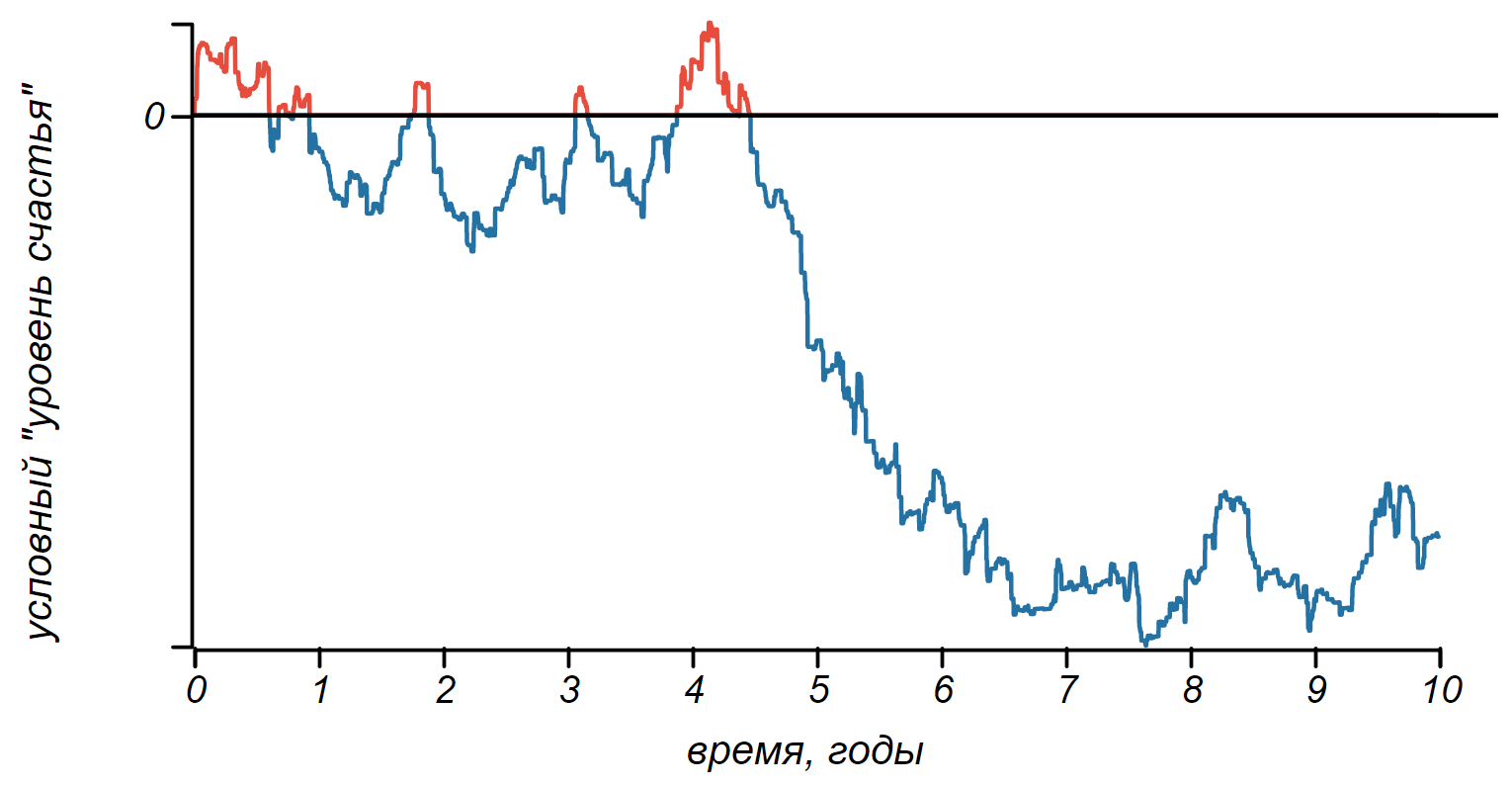
События, сливаясь в памяти, образуют эмоциональную окраску «синтетической жизни».
Ну, что же, мы уже видим какое-то чередование настроения, но картинка вышла не шибко радостной. Наш герой после череды смен настроения впал в глубочайшую депрессию. Жаль. Попробуем ещё несколько судеб. Все они испытывают череду светлых и тёмных полос, но надолго увязают либо в беспросветной тоске, либо в запредельном счастье. Так бывает, конечно, но это явно ненормально.
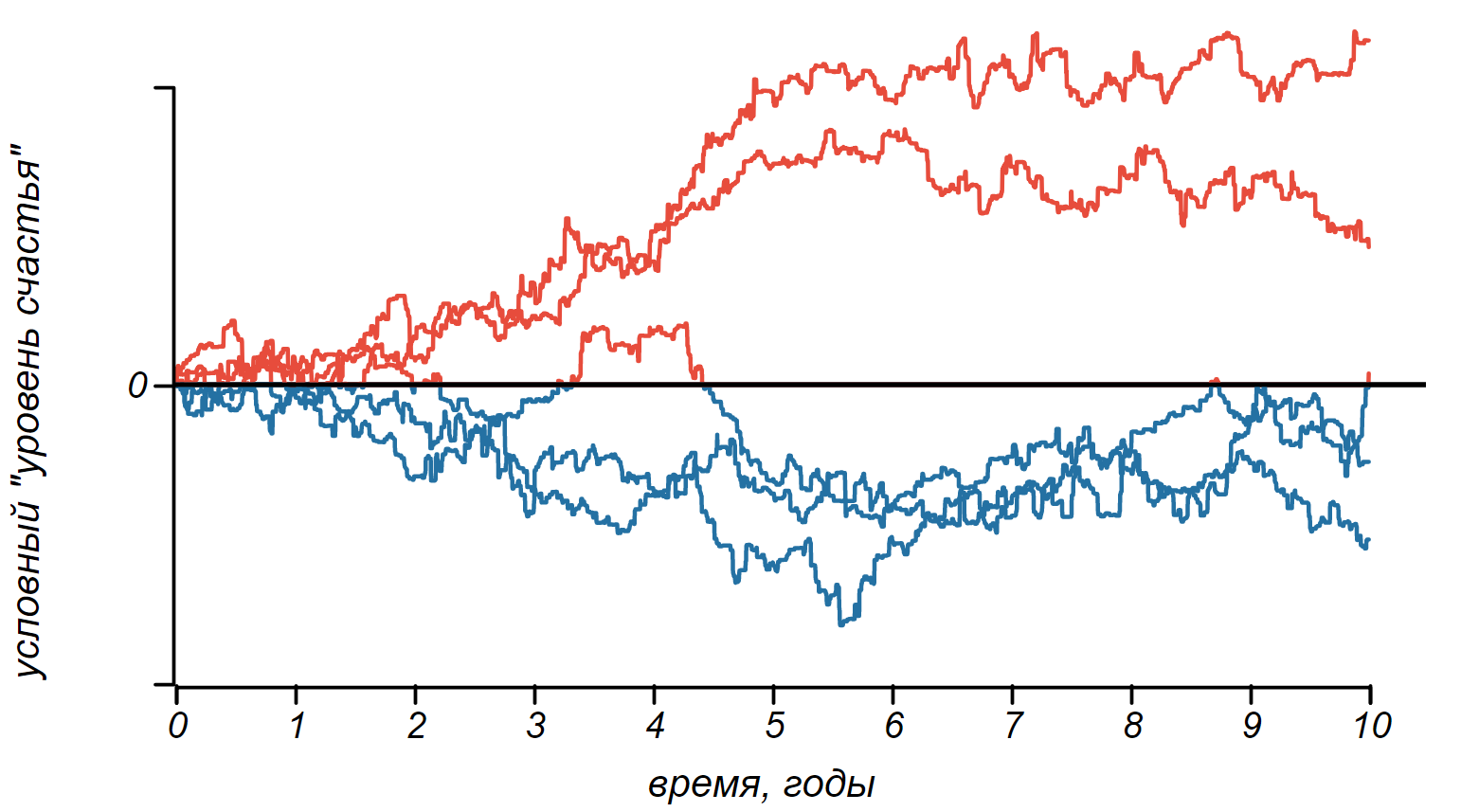
Несколько примеров «синтетических судеб» людей с идеальной памятью.
Relax, dude!
Наши модельные судьбы мы описали очень примечательным процессом, он зовется одномерным случайным блужданием и имеет ряд необычных свойств, среди которых — самоподобие, то есть, отсутствие какого-либо характерного временного масштаба. Кроме того, получив в своё распоряжение неограниченное время, случайное блуждание способно увести неограниченно далеко, и более того, оно обязательно уведёт вас на любое наперёд заданное расстояние о начального значения! Таким образом, какими бы ни были хорошими ваши дела, если они подчинены случайному блужданию, они обязательно скатятся до нуля и уйдут ниже, это просто вопрос времени! Этот известный и поучительный жизненный закон, получил имя проклятие игрока и его суть можно выразить простой максимой:
Оптимальная стратегия в азартных играх — владеть казино, в противном случае, вы проиграете.
Мы не будем подробно останавливаться на этом, уж больно известном результате, однако это свойство одномерного случайного блуждания нам ещё встретится.
Похоже, идеальная эмоциональная память это не очень хорошо. Наши герои не забывают ничего и тщательно хранят в памяти всё, даже самые давние события! На их настроении в старости влияет горе от поломанной игрушки в детстве или радость от поцелуя в юности. Причём все последующие поцелуи и игрушки имеют для них такую же важность. Надо этих бедолаг спасать. Эмоции со временем стихают, горе притупляется, радость, увы, тоже. Забывание, во многом, подобно остыванию, диффузии или замедлению движения в вязкой жидкости, поэтому разумно смоделировать его подобным образом. Перечисленные процессы называются процессами релаксации. Наделим же и наших бедолаг способностью к релаксации!
Релаксирующая система возвращается к равновесному состоянию, причём, тем быстрее, чем больше отклонение от равновесия. Это свойство можно смоделировать геометрической прогрессией, или экспоненциальным законом. Введём в нашу модель новый параметр — скорость забывания 
. Его можно выразить через время (в отсчетах нашей модели), за которое уровень эмоции уменьшится достаточно сильно. Например для 
эмоциональный след от события уменьшится на порядок через два месяца. И вот жизнь стала по-хорошему «полосатой»!
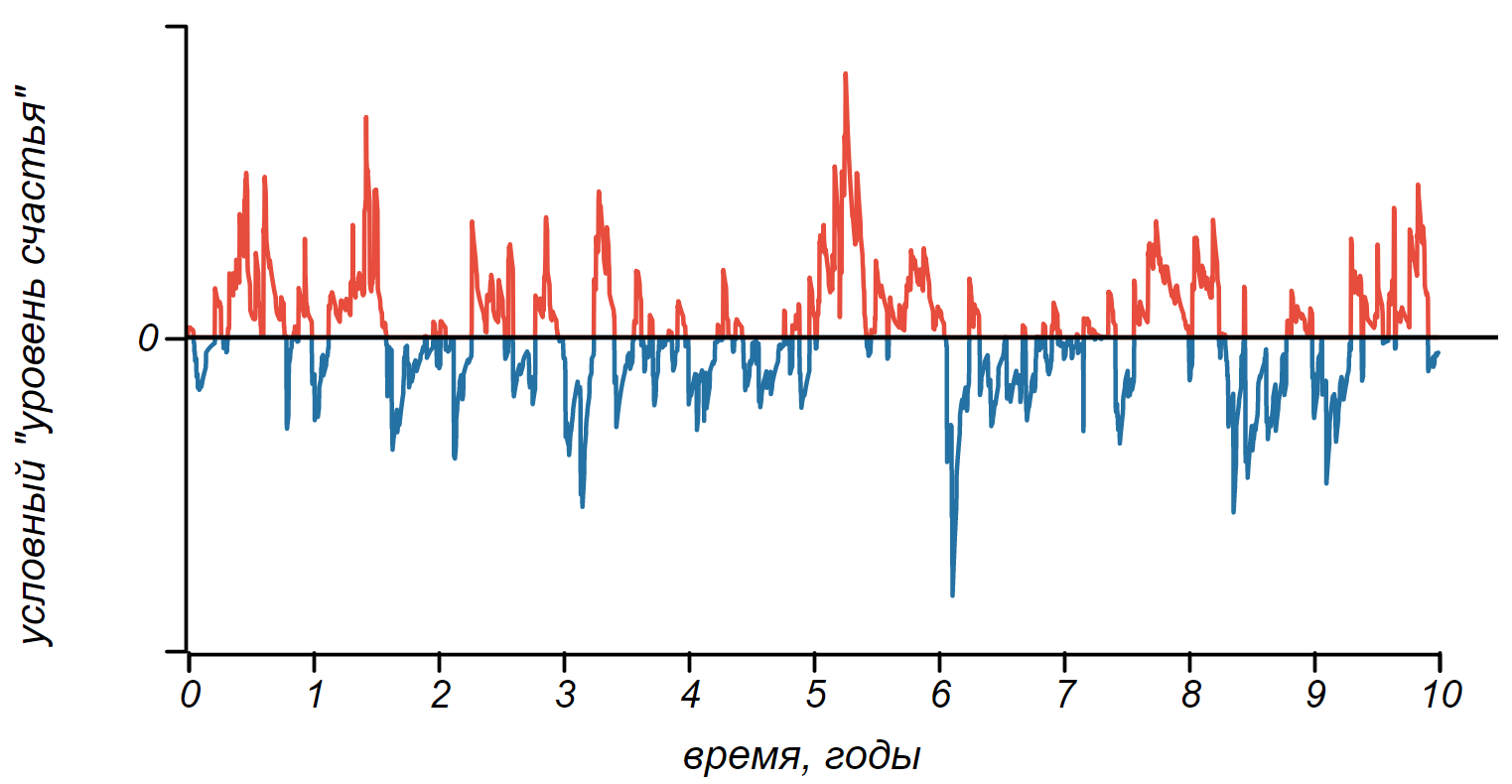
Ограничение памяти приводит к тому, что череда событий и их следов в памяти сливаясь, образуют череду эмоционально окрашенных полос.
Меняя «степень забывчивости», мы можем получить более или менее эмоционально уравновешенных подопытных. Кажется, мы нашли источник зеброобразности! Это, во-первых, случайные блуждания, склонные к расползанию во все стороны, и, во-вторых, целительная забывчивость, возвращающая настроение в норму. Результатом является волнообразное меандрирование настроения.
Давайте изучим свойства полученных нами «синтетических» житейских полос. Построим гистограмму, показывающую распределение их длительностей для длиннющей жизни (или для множества обычных) с параметрами 
.
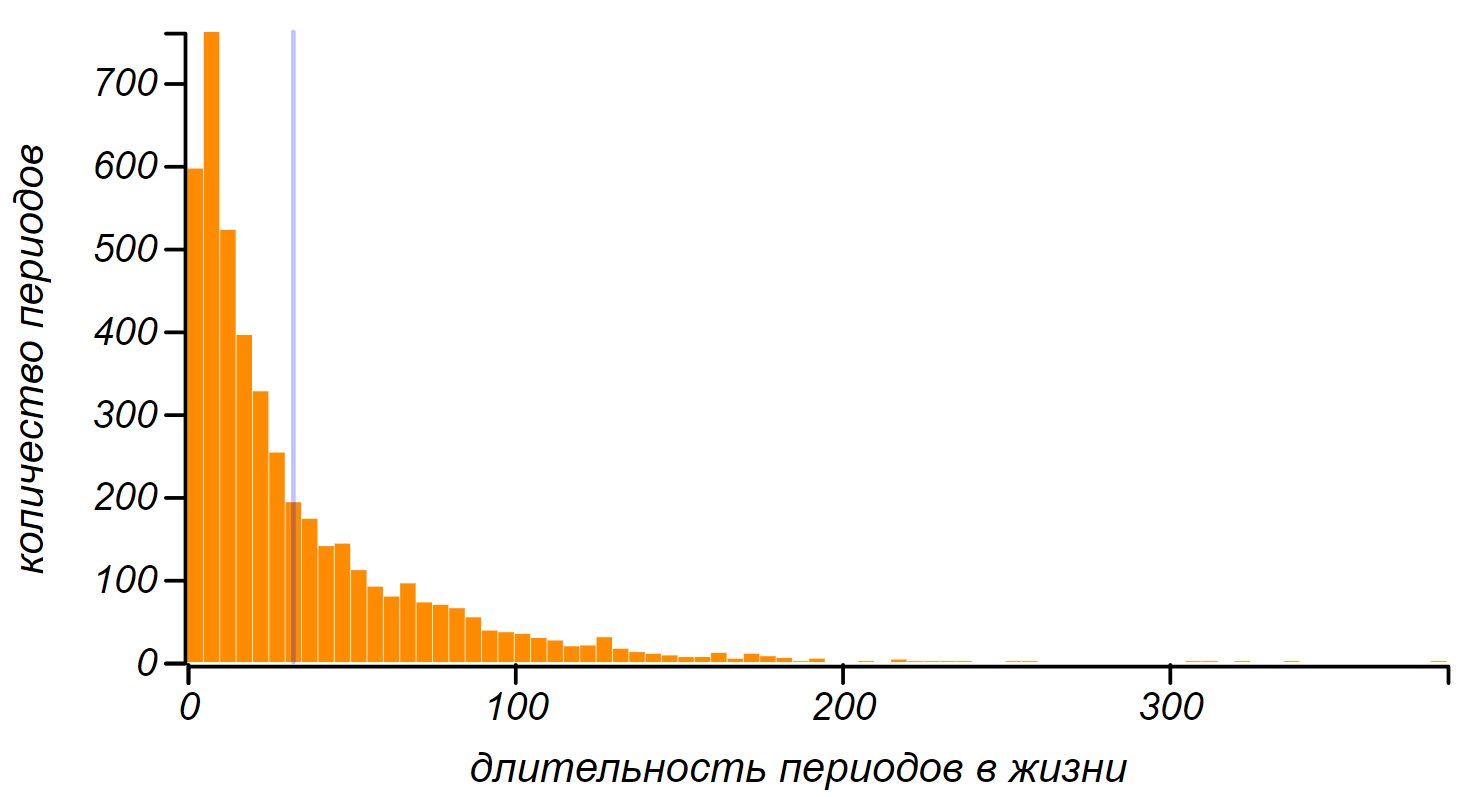
Распределение длительностей периодов счастья и горя для большого числа синтетических судеб. Вертикальной линией отмечено среднее значение, равное 33.
Первое, что бросается в глаза — максимум распределения (мода) находится вблизи нуля, значит, чаще всего периоды счастья и несчастья очень коротки, однако, встречаются и периоды длительностью более года. В среднем же, продолжительность периодов составляет 33 дня, со стандартным отклонением в 36 дней. Это распределение близко к экспоненциальному (на самом деле оно неплохо описывается более общим гамма распределением с такими параметрами, которые приближают его к экспоненциальному). В свою очередь, экспоненциальное распределение длительностей полос в жизни означает, что смены настроений можно рассматривать, как пуассоновский поток, то есть, как цепочку независимых случайных событий, не имеющих выделенной частоты, но случающихся с некоторой известной интенсивностью. Например, в рассмотренном нами примере тёмные и светлые полосы сменяются с интенсивностью раз в 33 дня, но при этом, больше всего в жизни наблюдается коротких периодов: половина их не длиннее десяти дней.
В случае отсутствия «памяти» (для 
), распределение перестаёт быть экспоненциально убывающим и становится степенным.
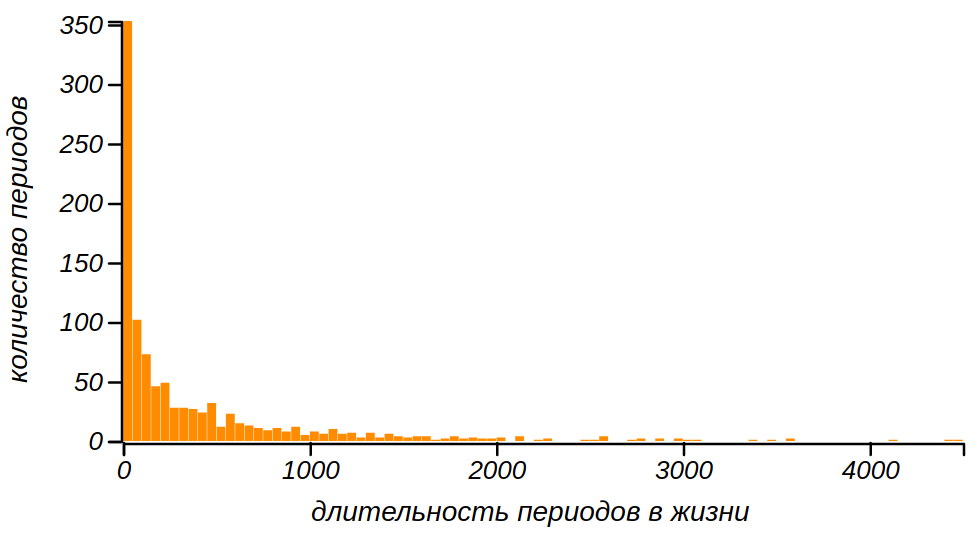
Распределение длительностей меандров для случайного блуждания имеет характер степенного распределения.
Статистики говорят, что у таких распределений тяжёлый хвост, делающий вполне вероятными очень большие отклонения от среднего значения, мы наблюдали их в виде долгих “погружений” в то иное настроение. У полученного нами распределения есть одно, непривычное и странное свойство — для него не определены ни среднее значение (математическое ожидание), ни стандартное отклонение, ни медиана. Дело в том, что все эти характеристики вычисляются исходя из площади под кривой плотности распределения, а она бесконечна. В связи с этим, можно услышать, что среднее значение в таком случае бесконечно, но это не так. Посмотрите, что произойдёт при попытке вычислить среднее значение длительности меандров случайного блуждания:
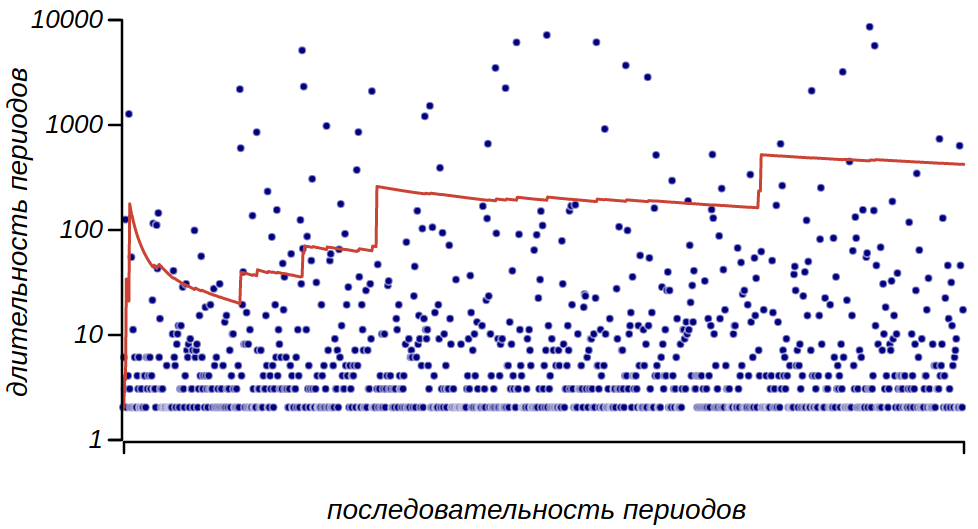
Попытка вычислить среднее значение для последовательности длительностей периодов между сменами настроения при отсутствии памяти. Появляющиеся экстремальные значения из тяжёлого хвоста распределения приводят к тому, что значение среднего не сходится к какому-либо значению.
Огромные скачки, происходящие из тяжёлого хвоста то и дело сбивают значение среднего и последовательность усреднений не сходится ни к какому пределу. Значение среднего вовсе не бесконечно, просто интеграл не сходится ни к какому числу и о каком-либо конкретном значении говорить нельзя. Именно в невозможности вычислить среднее значение длительности меандров отражается свойство самоподобия случайного блуждания, а именно отсутствие какого-либо собственного масштаба времени.
Мы моделировали приспосабливаемость к житейским неурядицам с помощью релаксации, или затухания эмоциональных всплесков. Можно истолковать этот процесс другим образом, как приспосабливаемость человека к жизненным обстоятельствам. При обработке зашумлённых сигналов или последовательностей часто для сглаживания и выделения полезного сигнала используют метод скользящего среднего, рассматривая в каждый момент не сам сигнал, а усреднённое значение сигнала в некоторый промежуток времени. Таким образом удаётся избавиться от шума и получить представление о долговременных тенденциях сигнала. Применяя такое усреднение к житейским неурядицам, мы можем моделировать приспосабливаемость человека. И во время войн люди влюбляются и находят повод для радости, так же как не безоблачна жизнь богатых бездельников. Смещается норма, от которой настроение отклоняется в ту или иную сторону. Рассматривая разницу между последовательность эмоций и сглаженной линией фона, мы получим такую же картину, полос, какую дала нам предыдущая модель, с теми же статистическими характеристиками. Это неудивительно, ведь концептуально они практически не отличаются, описывая систему с релаксацией.
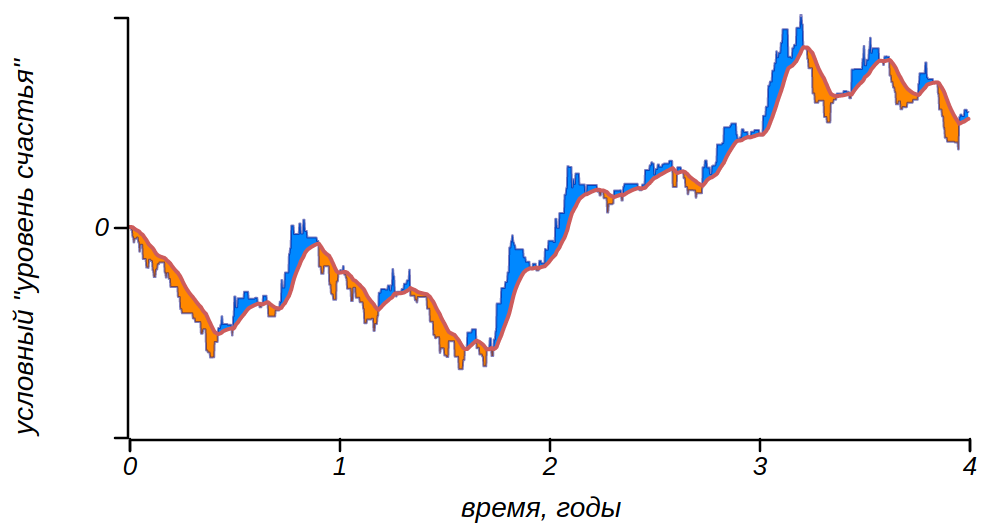
Меандрирование и смену настроений можно получить, моделируя скользящим средним приспосабливаемость человека к обстоятельствам.
Связанные одной цепью
В рассмотренных моделях мы получали пуассоновский поток смены настроений, генерируя события пуассоновским потоком. В этом можно усмотреть некоторую подтасовку — пуассоновский случайный процесс оказался «вшит» в модель. Насколько при этом универсален наш результат? Можно ли получить его как-нибудь по-другому?
Житейский опыт — штука плохо формализуемая, и его можно подогнать его под различные математические инструменты, допуская не только упрощающие допущения, но и спекуляции. В науке такой подход недопустим, но в нашем путешествии по методам теории случайных процессов, мы можем позволить себе поиграть с ними, чтобы познакомиться получше.
Наблюдая за динамикой настроения и мировосприятия можно заметить, что человеку свойственно «залипать» в определённом настроении. Если дела идут в целом хорошо, то и дурная новость может быть воспринята с оптимизмом. И, напротив, меланхолическое настроение, однажды поглотив человека, способно испортить даже радостное известие. С математической точки зрения, это значит, что вероятность остаться в текущем настроении больше вероятности его изменить. Такое поведение можно описать с помощью случайного процесса, называемого цепью Маркова. В общем случае, марковская цепь может быть представлена, как фиксированный набор состояний с переходами между ними, причём, переходы из состояния в состояние имеют различную но известную вероятность. Такие цепи удобно представлять в виде взвешенных графов, например, элементарная симметричная марковская цепь описывающая динамику настроения может быть представления таким образом:
Цепь Маркова с двумя состояниями («радостное» и «печальное»). Стрелки обозначают переходы и вероятности этих переходов. В нашем симметричном случае вероятность остаться в существующем настроении превышает вероятность его смены, но не зависит от самого настроения.
Наша цепь способна генерировать последовательности состояний и, конечно же, в ней появятся полосы житейской зебры.
Самой интересное, выяснить какому распределению будут подчиняться длительности этих полос. Для нашей более чем простой модели ответ можно получить точный — это геометрическое распределение, описывающее вероятность наблюдать заданное количество испытаний случайного эксперимента до наблюдения первого «успеха».
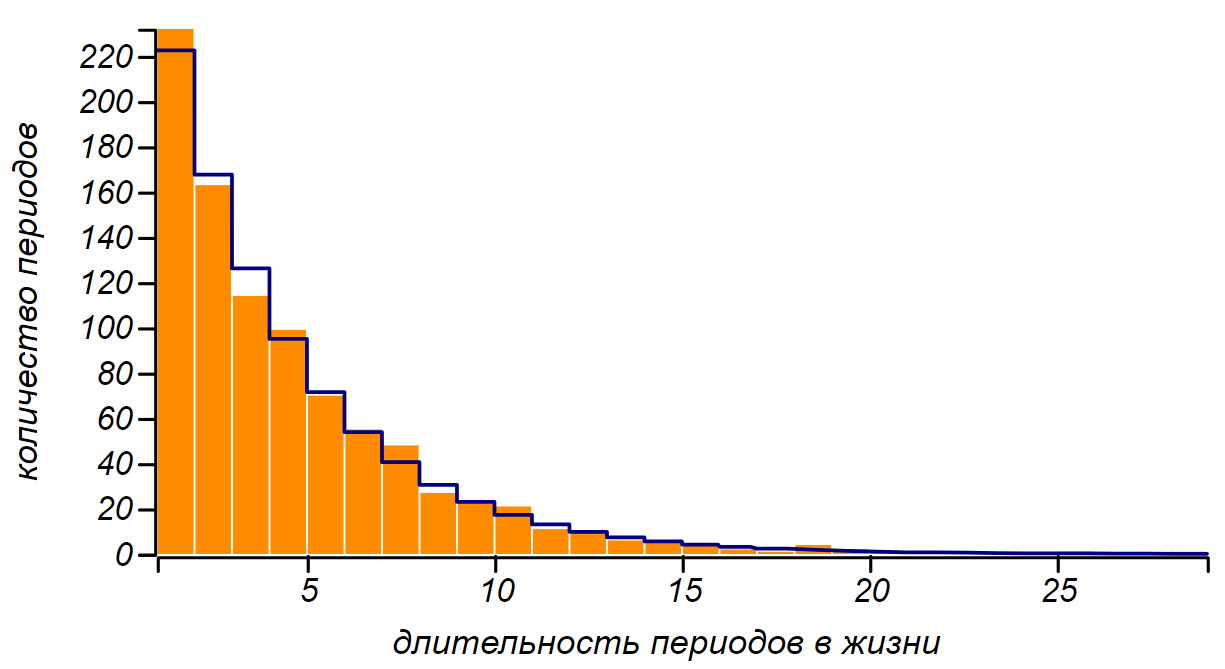
Гистограмма для длительностей периодов одинакового настроения в последовательности, генерированной симметричной цепью Маркова и функция вероятности геометрического распределения с параметром равным вероятности перехода между состояниями. Последовательность имеет длительность в десять лет.
Геометрическое распределение является дискретным аналогом экспоненциального распределения, в том смысле, что ему подчиняются округленные значения экспоненциально распределённой случайной величины. Существует связь между параметром геометрического распределения и интенсивностью соответствующего экспоненциального распределения. Таким образом, мы опять получаем пуассоновский поток смен настроения, и для описанной нами марковской цепи его интенсивность равна 
.
Если мы нарушим симметрию цепи, то сможем описать «оптимиста» либо «пессимиста», охотнее «залипающего» в том или ином настроении. Распределение длительностей полос при этом отклонится от геометрического, но при этом, всё равно, большая часть полос будет короткой. и какой-либо выделенной периодичности наблюдаться не будет.
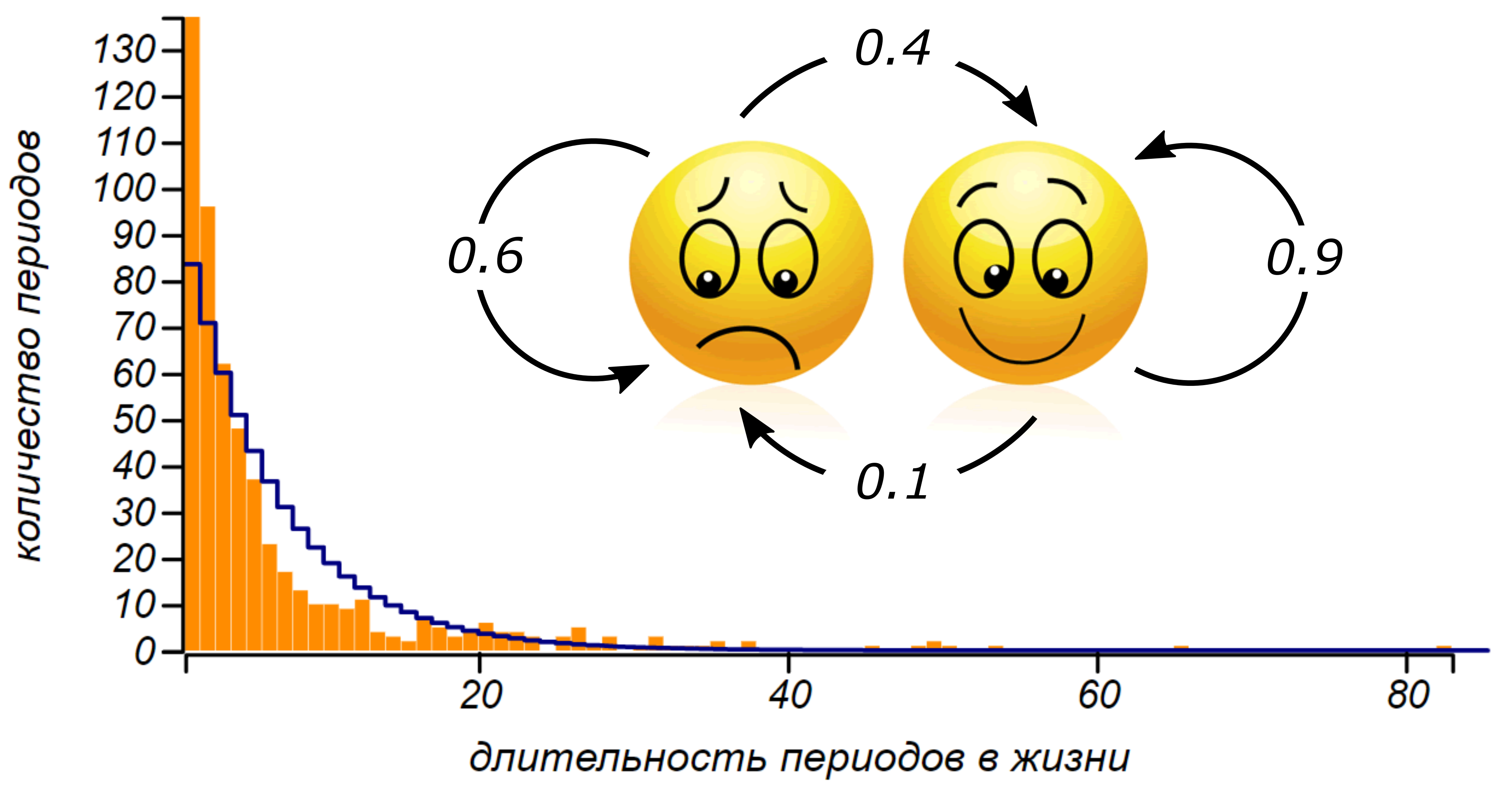
Гистограмма для длительностей периодов постоянного настроения в последовательности, генерированной асимметричной цепью Маркова. Последовательность имеет длительность в десять лет.
Цепи Маркова — это мощный инструмент анализа случайных процессов, в которых кроется некий алгоритм или сценарий. Они дают нам своеобразный взгляд на процессы, которые принято считать циклическими. Например известная максима: «история человечества ходит по кругу» часто трактуется как то, что в истории существуют некие циклы или даже периодичности. Приходится слышать, например, о том, что начало века сулит потрясения и войны. Рискуя забраться не в свою тему, возьму на себя смелость предположить, что на самом деле имеет смысл говорить не о буквальных циклах, а о более или менее устойчивых сценариях — закономерных цепочках, которые можно описать цепью Маркова. Среди марковских цепей есть класс циклических цепей, которые, в самом деле, способны создавать повторяющиеся последовательности. Однако настоящей детерминистической периодичности в их поведении нет. Случайно возникая в разные исторические периоды и в разных контекстах такие циклы похожи друг на друга, и могут создать ощущение исторического «дежа-вю». Изучать и описывать их полезно, но ожидать строгого календарного плана, пожалуй, не стоит.
На этом мы закроем тему зебры. Какие выводы можно сделать из нашего несерьёзного исследования? Череда светлых и тёмных полос в жизни не иллюзия, они есть на самом деле. Но в них нет особенных закономерностей. Чаще всего они коротки, но бывают и затяжными. Всё зависит от лёгкости характера и способности отпускать прошлое. Более того, если события в жизни будут случаться редко, то жизнь станет серой чередой исчезающих в прошлом воспоминаний. Так что в наших интересах запоминать прожитое, и в наших же силах сделать так, чтобы жизнь не становилась случайным блужданием. Мы можем сделать так, чтобы событий хороших становилось побольше и происходили они почаще, пусть даже они будут и незначительными. Лыжная прогулка, искренняя улыбка прохожего, билет на концерт, чашка горячего шоколада в холодный день, всё это поможет создавать положительный тренд и продлит светлую полосу в жизни. Правда, вслед за трендом потянется и среднее значение, так что неизбежные грустные события обязательно сменят настроение. Но не надо винить в этом своё счастье. Это не расплата за него, и не сглаз. Это свойство релаксирующих систем — склонность к колебаниям при стохастическом внешнем воздействии.
Про ожидание автобуса или землетрясения
Различие между частотой (периодом) и интенсивностью потока событий достаточно важно понимать, слушая новости или читая результаты научных исследований. Например, на сегодняшний день, сейсмологи, увы, не могут предсказать конкретное землетрясение: его время, место и силу. Зато наработаны методики долгосрочного сейсмического прогноза для какого-то региона, но их результаты формулируются на языке теории вероятностей, и что с ними делать не всегда очевидно.
Например, для Авачинского залива, на берегах которого расположен Петропавловск-Камчатский в 2018 году дан такой прогноз: «Суммарная вероятность землетрясений с магнитудой более 7.7, которые могут иметь силу 7-9 баллов в г. Петропавловск-Камчатский, может достигать на следующее пятилетие 52.3%.» Что это значит? Завтра тряхнёт? А когда? А где? Увы на такие прямые вопросы мы ответить пока не в силах. Точная интерпретация этого сообщения такая: интенсивность сейсмического потока сейчас такова, что в ближайшие 500 лет произойдёт примерно 52 землетрясения (при условии неизменности потока). Причём, через месяц прогноз может измениться. Интенсивность похожа, в каком-то смысле, на мгновенную скорость движения: чтобы измерить, что вы двигаетесь со скоростью в 60 км/ч не обязательно ехать целый час все 60 км. И, самое главное, данный учёными прогноз не говорит о том, что между землетрясениями проходит десять лет, как можно предположить, разделив 500 лет на 52 события. Таким образом, если на протяжении десяти лет не было сильных землетрясений, то это не значит, что оно произойдёт не сегодня-завтра. Оно произойдёт, конечно, но сколько именно придётся ждать, неизвестно.
Посмотрите на то, как меняется уровень сейсмической активности Камчатского региона на разных масштабах времени (изображение взято с сайта Монитора сейсмической активности Камчатского филиала Единой геофизической службы РАН)
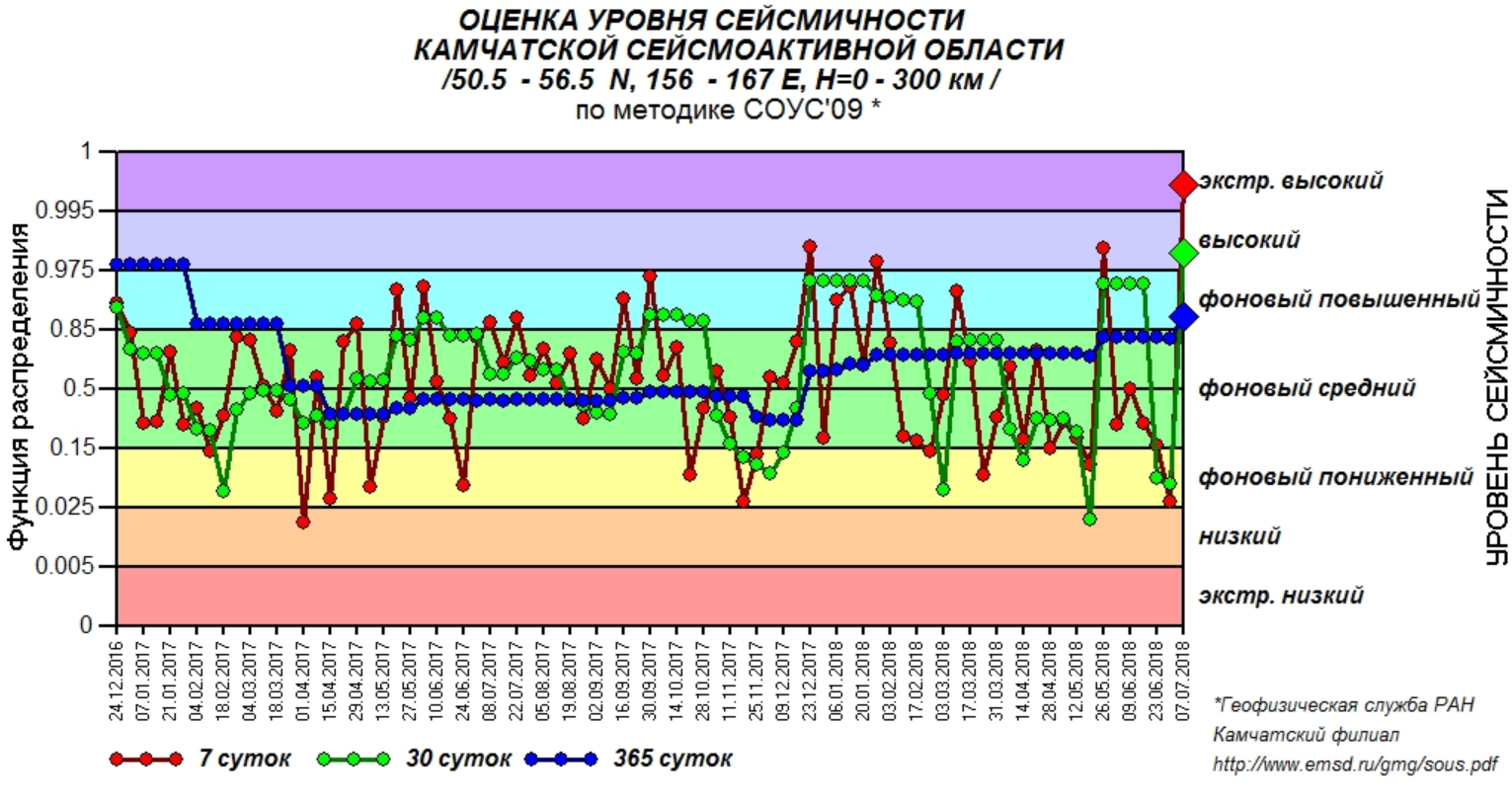
На смену пониженному уровню активности приходит повышенный, активность «дышит», но не периодично, а подобно всё тому же случайному блужданию с релаксацией.
Но землетрясения, всё же, неприятные явления и пусть бы их не случалось подольше. Бывают вещи, которых ждёшь с большим нетерпением, например, автобус. Приходя на остановку, мы, конечно, желаем мгновенно сесть на нужный маршрут автобуса или трамвая, но, скорее всего, это не удаётся. Тогда, если в этом месте действует чёткое расписание, мы смотрим на него, потом на часы, а потом погружаемся в книжку или телефон. Но часто, в середине маршрута, вместо расписания указывается интервал движения транспорта, например, 15 минут. Это значит, что мы уже далеко от автостанции, с которой автобусы выходят точно по расписанию, и накапливается некоторая ошибка, делающее прибытие автобуса случайным. Ну, 15, так 15, подождём. И вот тут надо иметь в виду, что в среднем придётся ждать именно 15 минут, независимо от того, когда вы приходите. Вот если бы автобусы приходили с периодичностью 15 минут, среднее время ожидания составило бы половину периода — 7,5 минут, но с интенсивностью так не выйдет! При отсутствии дополнительных условий, движение транспорта, моделируют пуассоновским потоком, а это значит, что время ожидания автобуса будет подчиняться экспоненциальному закону с той же интенсивностью. А математическое ожидание для экспоненциального распределённой величины с интенсивностью 
равно 
, таким образом и получается наш вывод. И что совсем обидно — то сколько времени вы уже провели на остановке никак не влияет на вероятность того, что автобус вот-вот подойдёт. Это работает такое свойство экспоненциального распределения, как отсутствие памяти, связанное с независимостью пуассоновских событий.
Подведём итог. Приходя на остановку, нужно чётко принять решение: ждать, или идти пешком, а размышлять на тему: подождать ещё или пойти уже пешком — только обрекать себя на встречу с законом подлости. Ибо когда вы, прождав уже 17 минут, плюнули, и пошли пешком, вас весьма вероятно обгонит долгожданный автобус, а то и два. Ну, и чтобы ожидание автобуса превратилось в томительное и безнадёжное состязание с судьбой, вспомним про проклятие велосипедиста из предыдущей главы, эффективно удлинняющее наблюдаемое время ожидания.
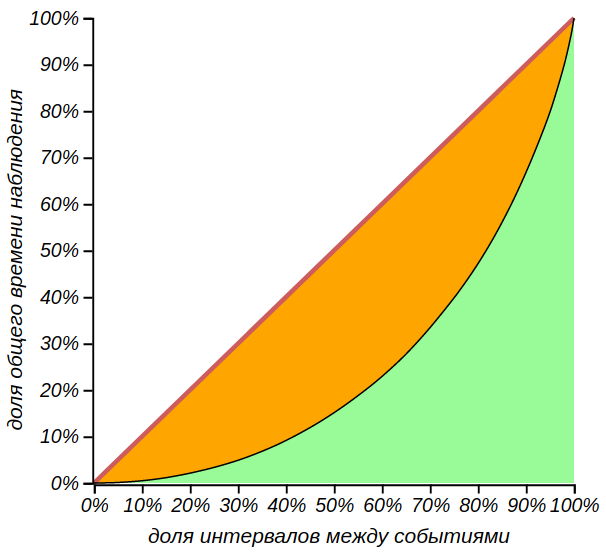
Интересно, что кривая Лоренца для экспоненциального распределения одинакова для любых интенсивностей. Таким образом, для всех пуассоновских процессов верно утверждение: половина общего времени наблюдения приходится на 20% случаев, когда это очередное событие задерживается. Коэффициент Джини для экспоненциального распределения равен в точности 1/2.
Чужая очередь
Я размышляю о законах подлости, стоя в аэропорту в очереди на регистрацию пассажиров и оформление багажа. Очередь длинная, люди разные и заметные со всеми своими сумками, детьми или клетками. Сзади слышу ворчание: «Как обычно, наша очередь тормозит. Вон, гляди, тот усатый в кепке наравне с нами стоял а теперь вон где… Вот ведь закон подлости! Всегда именно моя очередь медленная!» Этот закон зовётся наблюдением Этторе:
«Соседняя очередь всегда движется быстрее.»
Существует целая область теории управления и теории случайных процессов, которая занимается динамикой очередей. Это важно для проектирования магазинов и залов ожидания, оптимального управления операционным залом в банке, воротами на платную автостраду и документооборотом. И отправной точкой для моделирования очереди служит всё тот же пуассоновский поток, поскольку для него требуется минимум дополнительных допущений. Таким образом, перемещения того, кто стоит в очереди будет иметь вид монотонно растущей ступенчатой линии, с одинаковыми шагами, случающимися через случайные промежутки времени. Накопление данных таким образом называется пуассоновским процессом.
Вот так могут двигаться две длинные очереди:
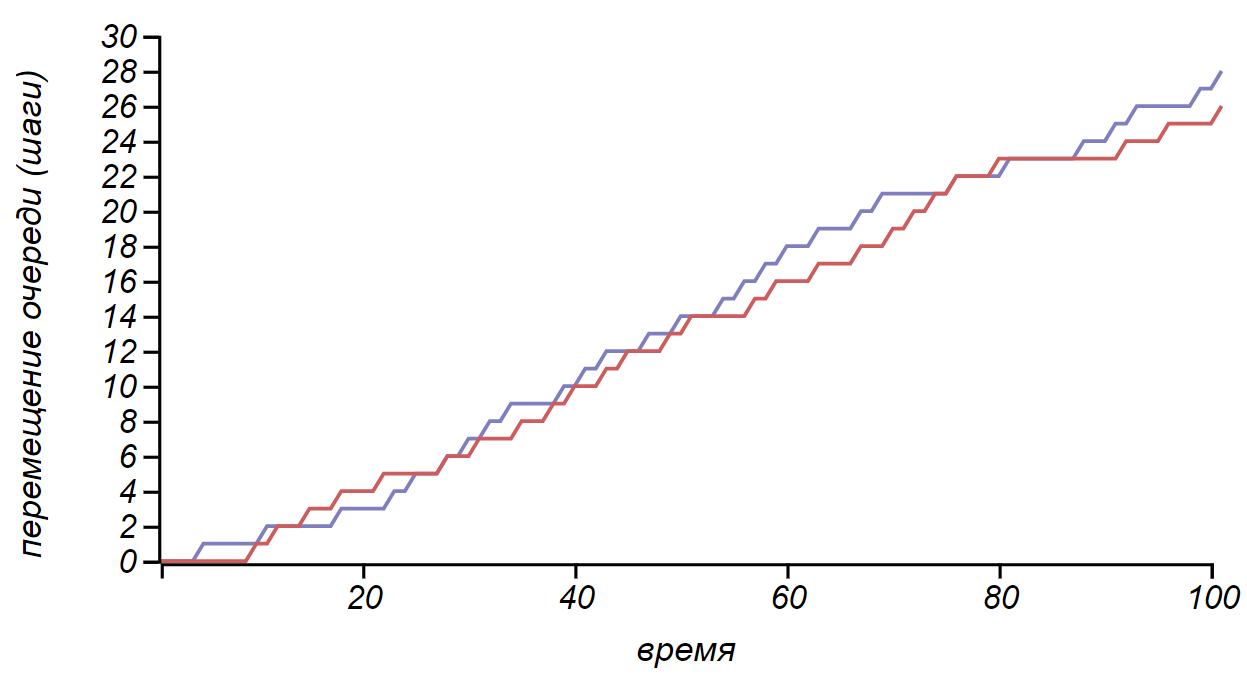
Перемещения двух соседних очередей, как пуассоновских процессов с равной интенсивностью.
В свою очередь, разница двух одинаковых пуассоновских процессов, а именно её наблюдает человек скучающий в хвосте, представляет собой своеобразное случайное блуждание. А раз так, то мы готовы сделать некоторые выводы. Первый: расстояние между одновременно вставшими в одинаковые очереди людьми будет то увеличиваться, то уменьшаться, при этом будут образовываться характерные меандры с постоянно меняющейся длительностью. Второй вывод: из-за самоподобия случайного блуждания и для коротких очередей и для длинных, меандры будут иметь длительность, соизмеримую со временем стояния в очереди, а значит, они будут заметны, а меандры — это уже повод для недовольства. Третий вывод: заранее неизвестно какая очередь пройдёт быстрее, ведь случайное блуждание равновероятно уходит как вверх, так и вниз. И, наконец, четвёртое заключение: очереди движутся независимо, то и дело опережая и нагоняя друг друга, в среднем, они движутся одинаково, и ожидаемая разница между ними стремится к нулю, но разброс вокруг среднего со временем растёт (в описанном нами случае, величина отставания одной очереди от другой подчиняется распределению Скеллама). Выходит, или угадал с быстрой очередью или нет — никаких подлых штучек со стороны злодейки судьбы!
Но законы подлости не назывались бы законами, если бы не претендовали на универсальность. Если нам не повезло оказаться в отстающей очереди, то мы в ней проведём больше времени и у нас будет больше возможностей посетовать на судьбу! А теперь, внимание, хорошие новости: в любой выбранный интервал времени тех, кому повезёт попасть в быструю очередь больше чем невезунчиков, ведь быстрая очередь может пропустить больше людей! Но, увы, это вовсе не утешит того, кто застрял в очереди.
Представленный текст ещё не издан, а это значит, что он может меняться. Я рассчитываю на то, что комментарии и замечания читателей Хабра помогут ему измениться в лучшую сторону.
Автор: Сергей Самойленко
