Сортировка слиянием на CUDA

Я решил изучить, как повысится производительность алгоритмов сортировки при их реализации на CUDA. Моя цель — понять, как можно использовать мощь параллельных вычислений для ускорения алгоритмов сортировки.

В качестве тестового я возьму алгоритм сортировки слиянием (merge sort), потому что он удобно разбивает задачу на меньшие подзадачи с двумя равными половинами, что хорошо подходит для параллельных вычислений.

Базовая рекурсивная сортировка слиянием сверху вниз

Ниже показана базовая логика сортировки слиянием сверху вниз, в которой я рекурсивно делю массив на две половины, пока не достигну базового случая из одного элемента, а затем выполняю слияние отсортированных половин.

Для слияния двух отсортированных массивов мы вычисляем их начальные элементы, выбираем меньший для выходного массива и двигаем указатели вперёд.

MERGE_SORT(arr, left, right)
    IF left < right THEN
        mid ← left + (right - left) / 2

        // Рекурсивно сортируем первую половину
        MERGE_SORT(arr, left, mid)

        // Рекурсивно сортируем вторую половину
        MERGE_SORT(arr, mid + 1, right)

        // Сливаем отсортированные половины
        MERGE(arr, left, mid, right)
    ENDIF
END MERGE_SORT

А теперь давайте взглянем на реализацию на CPU:

Code: Basic Recursive Merge Sort on CPU

▍ Примечания:

• Сигнатуры функций:
  • void merge(uint8_t* arr, uint8_t* temp, long long left, long long mid, long long right):
    • uint8_t вместо int для массивов элементов взят, чтобы значения оставались маленькими (0-255).
    • Использование long long для индексов позволяет использовать очень большие массивы (10¹⁸).
    • uint8_t* temp применяется как рабочее пространство для операции слияния, обеспечивая повышение производительности.
  • void mergeSort(uint8_t* arr, uint8_t* temp, long long left, long long right) соответствует псевдокоду, который разбивает массив на две половины и вызывает сам себя для этих двух половин. Когда он достигает базового случая (одного элемента), он вызывает функцию слияния для объединения двух половин.
• Разница сортировки на GPU и CPU:
  • Массивы генерируются с переданными аргументами и заданным seed (например, 1).
  • Все реализации выполняют примерно один и тот же объём работы.
  • Результаты сортировки слиянием необходимо вызвать обратно в исходный массив из GPU в CPU, что требует лишней траты ресурсов и сравнимо по производительности с массивом, отсортированным std::sort на CPU.
  • Возможно, лучше было бы сортировать случайные массивы на самом GPU и сравнивать результаты.
  • Способы и место сортировки во многом зависит от контекста использования.
• Для графиков используется физическое время выполнения всей программы, а не только время, потраченное на сортировку массива.
• Проверка корректности выполняется сортировкой исходного массива при помощи std::sort и сравнением результатов.
• Временная сложность для среднего случая: O(n log n).
• Пространственная сложность: O(n).

Базовая рекурсивная сортировка слиянием сверху вниз на CUDA

Теперь давайте посмотрим, как можно реализовать этот алгоритм на CUDA. Он следует тому же паттерну, что и реализация на CPU. Это моя первая наивная реализация на CUDA. Ядро запускается для каждой операции слияния, а рекурсия выполняется на CPU.

Code: Basic Recursive Merge Sort with CUDA

▍ Примечания:

• #include <cuda_runtime.h> предоставляет доступ к CUDA Runtime API и функциям типа cudaMalloc(), cudaMemcpy(), cudaFree(), kernel<<<numBlocks, threadsPerBlock>>>(args), cudaGetErrorString(), cudaGetLastError()
• __global__ void mergeSort(uint8_t* arr, uint8_t* temp, long long left, long long right) — это функция ядра, запускаемая для каждой операции слияния, которая пока делает то же самое, что и в реализации на CPU.
• В void mergeSort(....)
  • merge<<<1, 1>>>(...) запускает ядро для каждой операции слияния, но пока она просто запускает для выполнения всего слияния один поток, что неэффективно. <<<1,1>>> указывает количество блоков потока и количество потоков на каждый блок потоков. <<<numBlocks, blockSize>>> — это синтаксис для запуска ядра в CUDA. Суммарное количество потоков равно numBlocks * blockSize, и их можно выстраивать в 1D-, 2D- или 3D-сетку.
  • cudaDeviceSynchronize() заставляет ожидать завершения этого слияния, прежде чем переходить к следующему этапу, чтобы избежать проблем с корректностью.
  • cudaMalloc(....) используется для распределения памяти в GPU. cudaMemcpy(..., cudaMemcpyHostToDevice) и cudaMemcpy(...., cudaMemcpyDeviceToHost) можно использовать для копирования данных между CPU и GPU.
  • cudaFree(cu_arr) используется для освобождения памяти в GPU.

▍ Сравнение реализаций базовой рекурсивной сортировки слиянием на CPU и GPU

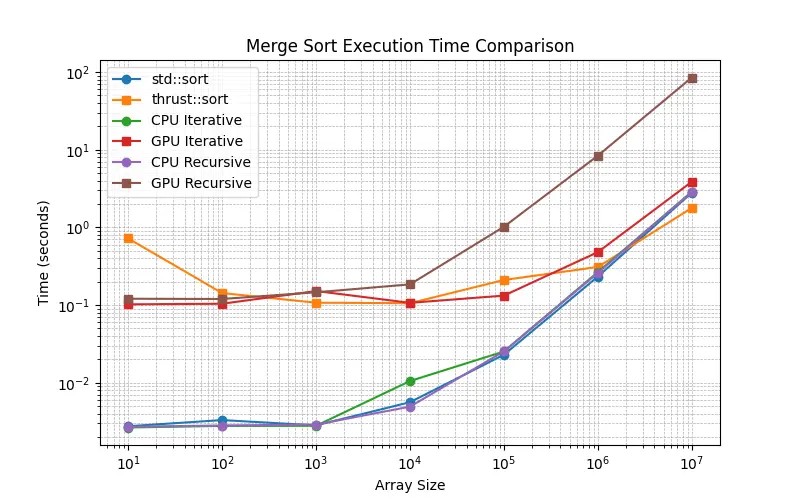
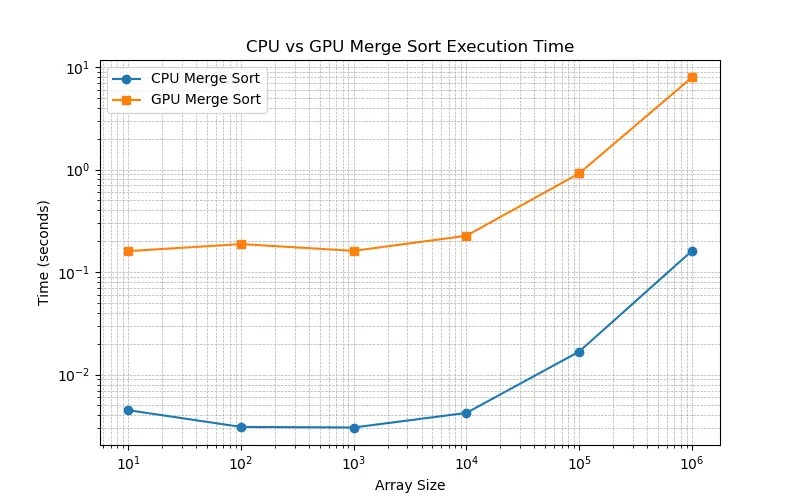
Как видно на Рисунке 1, эта реализация не особо эффективна: ядро запускается для каждой операции слияния, а рекурсия выполняется на CPU. CUDA не обрабатывает рекурсию эффективно, поэтому мы должны преобразовать рекурсию в цикл.

У меня возникли важные вопросы:

• Почему CUDA плохо справляется с рекурсией?
  • Наша функция слияния запускается как единственный поток на GPU, а рекурсия выполняется на CPU. Глубокую рекурсию создавать проблематично, потому что она может привести к переполнению стека, учитывая маленький размер потоков на GPU. Для каждой операции слияния есть существенная лишняя трата ресурсов на запуск ядра. Рекурсия не позволяет особо хорошо использовать параллелизм. Синхронизация тоже вызывает проблемы.
• Как мы можем улучшить ситуацию?
  • Переписать рекурсию в итеративный цикл и выполнять сортировку слиянием снизу вверх.

В отличие от реализаций на CPU, в которых широко применяется рекурсия, для обеспечения оптимальной производительности CUDA требует итеративного подхода с аккуратным управлением памятью и синхронизацией потоков; это видно из показанной ниже реализации.

Итеративная сортировка слиянием снизу вверх

Так как CUDA не может эффективно выполнять рекурсию из-за ограничений стека, мы реализуем для сортировки слиянием итеративный подход. Основой итеративного подхода будет слияние массива снизу вверх. Мы начинаем со слияния наименьших подмассивов размера 1, затем сливаем подмассивы размера 2, затем 4, 8, 16 и так далее.

MERGE_SORT(arr, temp, start, end)
    FOR sub_size ← 1 TO end STEP 2 × sub_size DO
        FOR left ← 0 TO end STEP 2 × sub_size DO
            mid ← MIN(left + sub_size - 1, end)
            right ← MIN(left + 2 × sub_size - 1, end)

            MERGE(arr, temp, left, mid, right)
        ENDFOR
    ENDFOR
END MERGE_SORT

А теперь давайте посмотрим реализацию на CPU:

Code: Iterative Merge Sort on CPU

▍ Примечания:

void mergeSort(uint8_t* arr, uint8_t* temp, long long n) {
    long long left, mid, right, size;
    for (size = 1; size < n; size *= 2) {
        for (left = 0; left < n - size; left += 2 * size) {
            mid = left + size - 1;
            right = std::min(left + 2 * size - 1, n - 1);
            mergeKernel(arr, temp, left, mid, right);
        }
    }
}

Мы превратили рекурсию в цикл:

• Верхний цикл for увеличивает размер с 1 до n по степеням двойки, так что мы получаем размеры 1,2,4,8. Могут возникнуть опасения, что размеры массивов неточно совпадут со степенями двойки; я решил эту проблему, ограничив индекс right концом массива.
• Внутренний цикл for проходит по массиву шагом в 2*size и выполняет слияние подмассивов размера size, начиная с left до right, а mid — это середина подмассива. Обратите внимание, что right = std::min(left + 2 * size - 1, n - 1);, что ограничивает правый индекс концом массива.
• mergeKernel эквивалентна функции merge в решении с рекурсией, но теперь она вызывается в цикле.

Итеративная сортировка слиянием снизу вверх на CUDA

Лично для меня самым важным уроком стала эта реализация. В приведённой выше реализации присутствуют два цикла, поэтому я решил, что можно выполнять второй цикл параллельно на GPU, ведь он в основном параллельно производит операции слияния для всего массива.

void mergeSort(uint8_t* arr, uint8_t* temp, long long n) {
    bool flipflop = true;
    long long numThreads, gridSize;
    long long size; // size - это размеры массивов слияния
    for (size = 1; size < n; size *= 2) {
        numThreads = max(n / (2 * size), (long long)1);
        gridSize = (numThreads + THREADS_PER_BLOCK - 1) / THREADS_PER_BLOCK;
        mergeKernel<<<gridSize, THREADS_PER_BLOCK>>>(flipflop ? arr : temp, flipflop ? temp : arr, size, n);
        CUDA_CHECK(cudaGetLastError());
        CUDA_CHECK(cudaDeviceSynchronize());
        flipflop = !flipflop;
    }

    if (!flipflop) CUDA_CHECK(cudaMemcpy(arr, temp, n * sizeof(uint8_t), cudaMemcpyDeviceToDevice));
}

▍ Примечания:

• flipflop используется для отслеживания того, какой массив является окончательным отсортированным, а какой рабочим пространством.
• numThreads — это количество потоков, которое необходимо запустить для операции слияния. gridSize — это количество блоков, которое нужно запустить.
• После вычисления размера массивов слияния:
  • При заданном размере массивов слияния операция слияния происходит для двух подмассивов размера size. Поэтому мне нужно запускать n / (2 * size) потоков (1 помогает в случаях, когда размер становится больше n/2).
  • gridSize вычисляется делением количества потоков на THREADS_PER_BLOCK и округлением вверх. Grid size — это количество блоков, которое нужно запустить.
  • В mergeKernel мы указываем gridSize и THREADS_PER_BLOCK для запуска ядра. mergeKernel<<<gridSize, THREADS_PER_BLOCK>>>(flipflop ? arr : temp, flipflop ? temp : arr, size, n);: обратите внимание на тернарный оператор для переключения между массивами, в котором arr и temp служат в качестве ping-pong buffer — на основании состояния flipflop мы считываем из одного и записываем в другой.
  • CUDA_CHECK(cudaGetLastError()); и CUDA_CHECK(cudaDeviceSynchronize()); используются для проверки на ошибки и чтобы ядро точно завершило исполнение до перехода на следующий этап.
• if (!flipflop) CUDA_CHECK(cudaMemcpy(arr, temp, n * sizeof(uint8_t), cudaMemcpyDeviceToDevice)); используется для копирования окончательного отсортированного массива обратно в исходный массив, если окончательный отсортированный массив находится в массиве temp.

Теперь давайте взглянем на mergeKernel:

__global__ void mergeKernel(uint8_t* arr, uint8_t* temp, long long curr_size, long long n) {
    long long index = blockIdx.x * blockDim.x + threadIdx.x;
    long long left = 2 * curr_size * index;
    if (left >= n) return; 

    long long mid = min(left + curr_size - 1, n - 1);
    long long right = min(left + 2 * curr_size - 1, n - 1);

    long long i = left, j = mid + 1, k = left;

    ///.... ниже идёт обычная логика слияния
}

▍ Примечания:

• Мне понадобилась куча времени, чтобы разобраться с индексацией и с тем, как правильно запускать ядро для операции слияния. Я запускаю 1D-сетки и 1D-блоки. blockIdx.x даёт блоку индекс, который может иметь значение 1,2,3,4,… а затем blockDim.x указывает количество потоков в блоке. blockIdx.x * blockDim.x после прибавления threadIdx.x (от 0 до THREADS_PER_BLOCK-1) даёт нам глобальный уникальный индекс потока.
• Теперь мы можем уникальным образом идентифицировать поток глобально и хотим дать ему уникальную подзадачу в зависимости от его index. Перейдём к вычислению индексов left, mid и right для подмассива, слияние которого хотим выполнить. У нас есть массив размера n, каждый поток должен работать с подзадачами размера 2 * curr_size, начиная с left до right.
• Самый важный вопрос: сколько индексов у меня получилось? index= blockIdx.x * blockDim.x + threadIdx.x и если blockIdx.x равен 0 и threadIdx.x равен 0, то минимальный индекс будет равен 0. Мы знаем, что максимальный blockIdx.x равен gridSize-1. Так что максимальный индекс равен (gridSize-1) * blockDim.x + blockDim.x - 1, то есть gridSize * blockDim.x -1. Если заменить gridSize на numThreads + THREADS_PER_BLOCK -1 / THREADS_PER_BLOCK, а blockDim.x на THREADS_PER_BLOCK, то мы получим numThreads + THREADS_PER_BLOCK - 2. То есть максимальный индекс для решения наших подзадач с несколькими дополнительными потоками приблизительно равен n / 2 × curr_size​.
• Учитывая, что у нас есть индексы от 0 до n/2 * curr_size, можно вычислить left index как 2 * curr_size * index, что приблизительно охватывает весь массив. Если left >= n, то мы выполняем возврат, потому что охватили весь массив. У меня возник интересный пограничный случай: этот left ранее был int, это приводило к переполнению, и мне пришлось поменять его на long long. Я обнаружил эту ошибку при помощи compute-sanitizer и отладочных символов, использовав -g -G при компиляции через nvcc.
• После нахождения left, mid и right остаётся та же самая старая логика слияния.
• Я пробовал разные значения THREADS_PER_BLOCK, но результаты оставались почти одинаковыми.

Результаты

Мы определили задачу генерации случайных массивов на CPU, выполнения сортировки на CPU/GPU, а затем сравнили результаты со стандартной сортировкой std::sort на CPU.

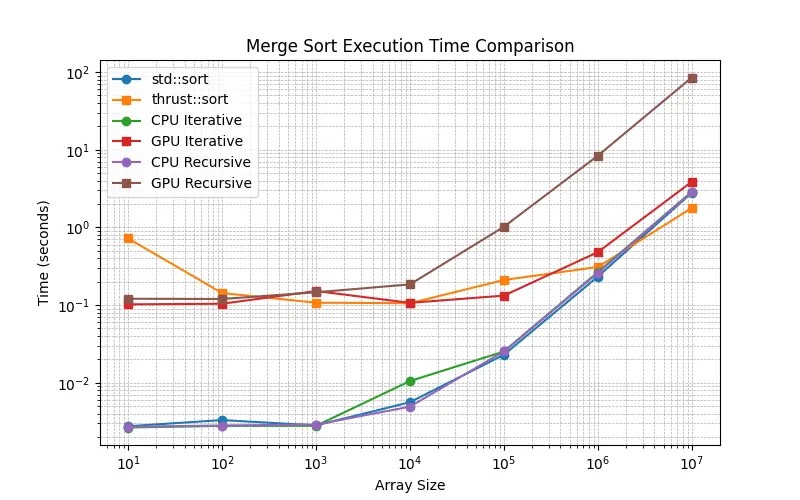
• Итеративная сортировка слиянием снизу вверх на CUDA существенно повышает эффективность благодаря распараллеливанию операций.
• Неудивительно, что решения на CPU проявляют себя лучше на маленьких массивах при замере физического времени выполнения программы.
• thrust::sort оказывается для больших массивов лучше, чем мои реализации: итеративный способ на GPU вполне конкурентоспособен, а рекурсивный способ сильно отстаёт.
• Решения на CPU, то есть рекурсивный и итеративный, очень конкурентоспособны по сравнению с std::sort
• 10⁷ — это точка перегиба, в которой сортировка на GPU с помощью thrust::sort начинает побеждать стандартную сортировку на CPU, а моя итеративная реализация на GPU тоже к ней приближается.
• Вероятно, причиной различий времени между решениями на CPU и GPU при размерах от 10¹ до 10⁴ стала трата ресурсов на отправку данных в GPU и возврат данных из GPU.

Заключение и дальнейшая работа

Я получил множество новых знаний о сортировке слиянием, которые долгое время ускользали от меня. Кроме того, этот простой алгоритм позволил мне изучить основы CUDA на среднем уровне сложности. Можно было многое сделать лучше, и это нужно будет исследовать в будущем:

• Лучше определять задачи или создавать большее количество задач со следующими целями:
  • Операции должны начинаться в CPU и оказываться в GPU только для дальнейших вычислений.
  • Операции должны начинаться и завершаться только на отдельных устройствах.
  • Операции должны начинаться в GPU и переходить в CPU только для дальнейших вычислений.
• Попытаться реализовать параллельную сортировку слиянием, предложенную Rezaul Chowdhury в источнике [1]
• Сравнивать массивы гораздо большего размера, начиная с 107 до 1018 и выполнять нагрузочное тестирование объёма сортировки, который мы можем выполнить на устройствах.
• Выполнить дальнейшую оптимизацию производительности на GPU при помощи общей памяти, thrust:sort на конкретном уровне в сочетании с моей реализации.
• Использовать потоки в реализации на CPU, чтобы проверить, полезно ли это будет для повышения производительности.
• Сравнить влияние выбора разных размеров THREAD_PER_BLOCK и, возможно, попробовать использовать каждый поток для решения не одной, а нескольких подзадач, поскольку мы ожидаем, пока закончат работу все потоки.

Ссылки

• Заметки Rezaul Chowdhury
• GeeksForGeeks: MergeSort
• NVIDIA CUDA Intro
• MergeSort на YouTube

Дополнительные источники

• Linebender GPU Sorting
• Onesweep Paper
• Onesweep GPU Code by Thomas Smith
• NVIDIA OneSweep
• Approachable Radix Sort Introduction
• Radix Sort by Thomas Smith
• Loop unrolling and thread coarsening
• Bitonic Sort implementation
• Bitonic Sort 2