Привет, Хаброжители! Книга закладывает фундамент для дальнейшего овладения технологией глубокого обучения. Она начинается с описания основ нейронных сетей и затем подробно рассматривает дополнительные уровнии архитектуры.
Книга специально написана с намерением обеспечить минимально возможный порог входа. Вам не требуются знания линейной алгебры, численных методов, выпуклых оптимизаций и даже машинного обучения. Все, что потребуется для понимания глубокого обучения, будет разъясняться по ходу дела.
Предлагаем ознакомится с отрывком «Что такое фреймворк глубокого обучения?»
Хорошие инструменты уменьшают количество ошибок, ускоряют разработку и увеличивают скорость выполнения
Если вы много читали о глубоком обучении, то наверняка сталкивались с такими известными фреймворками, как PyTorch, TensorFlow, Theano (недавно был объявлен устаревшим), Keras, Lasagne и DyNet. В последние несколько лет фреймворки развивались очень быстро, и, несмотря на то что все эти фреймворки распространяются бесплатно и с открытым исходным кодом, в каждом из них присутствует дух состязания и товарищества.
До сих пор я избегал обсуждения фреймворков, потому что, прежде всего, для вас крайне важно было понять, что происходит за кулисами, реализовав алгоритмы вручную (с использованием только библиотеки NumPy). Но теперь мы начнем пользоваться такими фреймворками, потому что сети, которые мы собираемся обучать, — сети с долгой краткосрочной памятью (LSTM) — очень сложны, и код, реализующий их с использованием NumPy, сложно читать, использовать и отлаживать (градиенты в этом коде встречаются повсеместно).
Именно эту сложность призваны устранить фреймворки глубокого обучения. Фреймворк глубокого обучения может существенно снизить сложность кода (а также уменьшить количество ошибок и повысить скорость разработки) и увеличить скорость его выполнения, особенно если для обучения нейронной сети использовать графический процессор (GPU), что может ускорить процесс в 10–100 раз. По этим причинам фреймворки используются в сообществе исследователей почти повсеместно, и понимание особенностей их работы пригодится вам в вашей карьере пользователя и исследователя глубокого обучения.
Но мы не будем ограничивать себя рамками какого-то конкретного фреймворка, потому что это помешает вам узнать, как работают все эти сложные модели (такие, как LSTM). Вместо этого мы создадим свой легковесный фреймворк, следуя последним тенденциям в разработке фреймворков. Следуя этим путем, вы будете точно знать, что делают фреймворки, когда с их помощью создаются сложные архитектуры. Кроме того, попытка самостоятельно создать свой небольшой фреймворк поможет вам плавно перейти к использованию настоящих фреймворков глубокого обучения, потому что вы уже будете знать принципы организации программного интерфейса (API) и его функциональные возможности. Мне это упражнение очень пригодилось, а знания, полученные при создании собственного фреймворка, оказались как нельзя кстати при отладке проблемных моделей.
Как фреймворк упрощает код? Если говорить абстрактно, он избавляет от необходимости снова и снова писать один и тот же код. А конкретно, наиболее удобной особенностью фреймворка глубокого обучения является поддержка автоматического обратного распространения и автоматической оптимизации. Это позволяет писать только код прямого распространения, а фреймворк автоматически позаботится об обратном распространении и коррекции весов. Большинство современных фреймворков упрощают даже код, реализующий прямое распространение, предлагая высокоуровневые интерфейсы для определения типичных слоев и функций потерь.
Введение в тензоры
Тензоры — это абстрактная форма векторов и матриц
До этого момента в качестве основных структур мы использовали векторы и матрицы. Напомню, что матрица — это список векторов, а вектор — список скаляров (отдельных чисел). Тензор — это абстрактная форма представления вложенных списков чисел. Вектор — это одномерный тензор. Матрица — двумерный тензор, а структуры с большим числом измерений называются n-мерными тензорами. Поэтому начнем создание нового фреймворка глубокого обучения с определения базового типа, который назовем Tensor:
import numpy as np
class Tensor (object):
def __init__(self, data):
self.data = np.array(data)
def __add__(self, other):
return Tensor(self.data + other.data)
def __repr__(self):
return str(self.data.__repr__())
def __str__(self):
return str(self.data.__str__())
x = Tensor([1,2,3,4,5])
print(x)
[1 2 3 4 5]
y = x + x
print(y)
[2 4 6 8 10]Это первая версия нашей базовой структуры данных. Обратите внимание, что всю числовую информацию она хранит в массиве NumPy (self.data) и поддерживает единственную тензорную операцию (сложение). Добавить дополнительные операции совсем несложно, достаточно добавить в класс Tensor дополнительные функции с соответствующей функциональностью.
Введение в автоматическое вычисление градиента (autograd)
Прежде мы выполняли обратное распространение вручную. Теперь сделаем его автоматическим!
В главе 4 мы познакомились с производными. С тех пор мы вручную вычисляли эти производные в каждой новой нейронной сети. Напомню, что достигается это обратным перемещением через нейронную сеть: сначала вычисляется градиент на выходе сети, затем этот результат используется для вычисления производной в предыдущем компоненте, и так далее, пока для всех весов в архитектуре не будут определены правильные градиенты. Эту логику вычисления градиентов тоже можно добавить в класс тензора. Ниже показано, что я имел в виду.
import numpy as np
class Tensor (object):
def __init__(self, data, creators=None, creation_op=None):
self.data = np.array(data)
self.creation_op = creation_op
self.creators = creators
self.grad = None
def backward(self, grad):
self.grad = grad
if(self.creation_op == "add"):
self.creators[0].backward(grad)
self.creators[1].backward(grad)
def __add__(self, other):
return Tensor(self.data + other.data,
creators=[self,other],
creation_op="add")
def __repr__(self):
return str(self.data.__repr__())
def __str__(self):
return str(self.data.__str__())
x = Tensor([1,2,3,4,5])
y = Tensor([2,2,2,2,2])
z = x + y
z.backward(Tensor(np.array([1,1,1,1,1])))Этот метод вводит два новшества. Во-первых, каждый тензор получает два новых атрибута. creators — это список любых тензоров, использовавшихся для создания текущего тензора (по умолчанию имеет значение None). То есть если тензор z получается сложением двух других тензоров, x и y, атрибут creators тензора z будет содержать тензоры x и y. creation_op — сопутствующий атрибут, который хранит операции, использовавшиеся в процессе создания данного тензора. То есть инструкция z = x + y создаст вычислительный граф с тремя узлами (x, y и z) и двумя ребрами (z -> x и z -> y). Каждое ребро при этом подписано операцией из creation_op, то есть add. Этот граф поможет организовать рекурсивное обратное распространение градиентов.
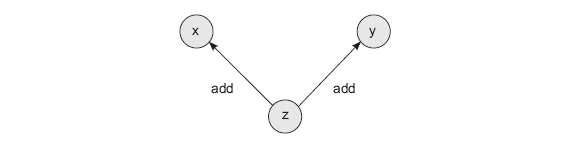
Первым новшеством в этой реализации является автоматическое создание графа при выполнении каждой математической операции. Если взять z и выполнить еще одну операцию, граф будет продолжен в новой переменной, ссылающейся на z.
Второе новшество в этой версии класса Tensor — возможность использовать граф для вычисления градиентов. Если вызвать метод z.backward(), он передаст градиент для x и y с учетом функции, с помощью которой создавался тензор z (add). Как показано в примере выше, мы передаем вектор градиентов (np.array([1,1,1,1,1])) в z, а тот применяет его к своим родителям. Как вы наверняка помните из главы 4, обратное распространение через сложение означает применение сложения при обратном распространении. В данном случае у нас есть только один градиент для добавления в x и y, поэтому мы копируем его из z в x и y:
print(x.grad)
print(y.grad)
print(z.creators)
print(z.creation_op)
[1 1 1 1 1]
[1 1 1 1 1]
[array([1, 2, 3, 4, 5]), array([2, 2, 2, 2, 2])]
addСамой замечательной особенностью этой формы автоматического вычисления градиента является то, что она работает рекурсивно — каждый вектор вызывает метод .backward() всех своих родителей из списка self.creators:
» Более подробно с книгой можно ознакомиться на сайте издательства
» Оглавление
» Отрывок
Для Хаброжителей скидка 25% по купону — Глубокое обучение
По факту оплаты бумажной версии книги на e-mail высылается электронная книга.
Автор: ph_piter
