Одним из самых ценных ресурсов любой социальной сети является "граф дружб" — именно по связям в этом графе распространяется информация, к пользователям поступает интересный контент, а к авторам контента конструктивный фидбэк. При этом граф является еще и важным источником информации, позволяющим лучше понять пользователя и непрерывно совершенствовать сервис. Однако в тех случаях когда граф разрастается, технически извлекать из него информацию становится все сложнее и сложнее. В данной статье мы поговорим о некоторых трюках, используемых для обработки больших графов в OK.ru.
Для начала рассмотрим простую задачу из реального мира: определить возраст пользователя. Знание возраста позволяет социальной сети подбирать более релевантный контент и лучше адаптироваться под человека. Казалось бы, возраст и так указывается при создании страницы в соцсети, но на самом деле достаточно часто пользователи лукавят и указывают возраст отличный от реального. Помочь исправить ситуацию может социальный граф :).
Возьмем, к примеру, Боба (все персонажи в статье вымышлены, любые совпадения с реальностью есть плод творчества рандома):

С одной стороны, половина друзей Боба являются подростками, что позволяет предположить что Боб также является подростком. Но у него есть и более старшие друзья, поэтому уверенность в ответе низкая. Помочь уточнить ответ может дополнительная информация из социального графа:

Добавив в рассмотрение не только дуги, в которых Боб принимает непосредственное участие, но и дуги между его друзьями, мы можем увидеть, что Боб является частью плотного сообщества подростков, что позволяет сделать вывод о его возрасте с большей степенью уверенности.
Подобная структура данных известна как ego network или эго подграф, она достаточно давно и успешно применяется при решении многих задач: поиск сообществ, определение ботов и спама, рекомендации друзей и контента и т.д. Однако расчет эго подграфа для всех пользователей в графе с сотнями миллионов узлов и десятками миллиардов дуг сопряжен с рядом "небольших технических затруднений" :).
Основная проблема заключается в том, что при рассмотрении информации о "втором шаге" в графе происходит квадратичный взрыв количества связей. Например, для пользователя со 150 прямыми связями эго подграф может включать до 
Дополнительной сложностью является тот факт, что граф хранится в распределенной среде, и ни один узел не имеет полного образа графа в памяти. Работы по balanced graph partitioning ведутся как в академии, так и в индустрии, но даже самые топовые результаты при сборе эго подграфа приводят к коммуникации "все со всеми": для того чтобы получить информацию о друзьях друзей пользователя, придется сходить на все "партиции" в большинстве случаев.
Одной из рабочих альтернатив в этом случае будет принудительное дублирование данных (например алгоритм 3 в статье от Google), но это дублирование тоже дается не бесплатно. Давайте попробуем разобраться, что можно улучшить в этом процессе.
Наивный алгоритм
Для начала рассмотрим "наивный" алгоритм генерации эго подграфа:
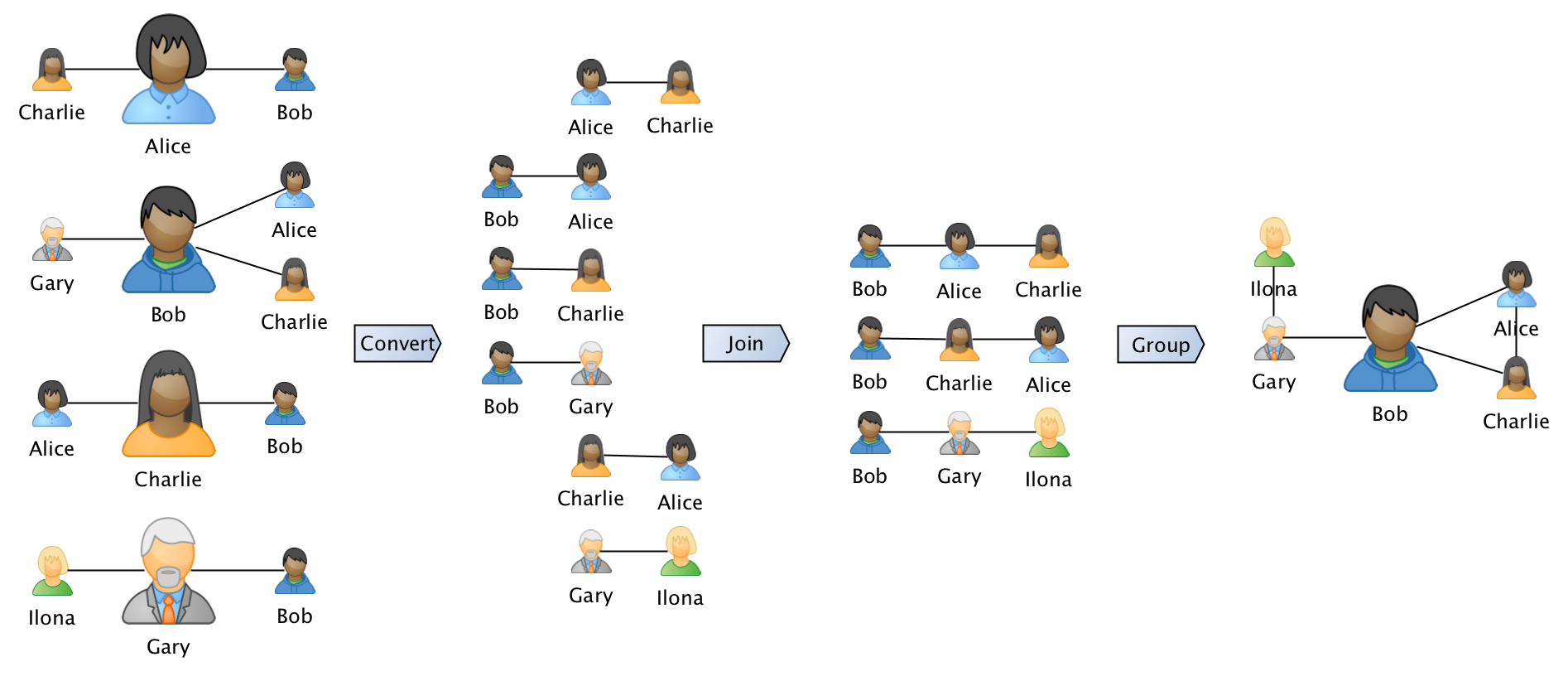
Алгоритм предполагает, что исходный граф хранится в виде списка смежности, т.е. информация о всех друзьях пользователя хранится в единой записи с ID пользователя в ключе и списком ИД друзей в значении. Для того чтобы сделать второй шаг и получить информацию о друзьях нужно:
- Преобразовать граф в формат списка ребер, где каждое ребро является отдельной записью.
- Сделать join списка ребер самого на себя, что даст все пути в графе длины 2.
- Сгруппировать по началу пути.
На выходе для каждого пользователя мы получаем списки путей длины 2 для каждого из пользователей. Здесь следует отметить, что полученная структура на самом деле является двухшаговой окрестностью пользователя, тогда как эго подграф является её подмножеством. Поэтому для завершения процесса нам нужно отфильтровать все выходящие вне непосредственных друзей дуги.
Этот алгоритм хорош тем, что реализуется в две строчки на Scala под Apache Spark. Но на этом преимущества заканчиваются: для графа промышленного размера объем сетевой коммуникации запредельный и время работы измеряется днями. Основную сложность создают две операции shuffle, которые происходят, когда мы делаем join и группировку. Можно ли уменьшить количество пересылаемых данных?
Эго подграф в один shuffle
С учетом того, что наш граф дружб симметричен, можно воспользоваться оптимизациями, предложенной Tomas Schank:
- Получить все пути длины 2 можно без join — если у Боба в друзьях Элис и Гарри, то существуют пути Элис-Боб-Гарри и Гарри-Боб-Алиса.
- При проведении группировки два пути на входе соответствуют одному и тому же новому ребру. Путь Боб-Алиса-Дэйв и Боб-Дэйв-Алиса содержит одну и ту же информацию для Боба, значит можно посылать только каждый второй путь, отсортировав пользователей по их ID.
После применения оптимизаций схема работы будет выглядеть так:

- На первом этапе генерации мы получаем список путей длины 2 с фильтром на порядок ID.
- На втором группируем по первому пользователю в пути.
В такой постановке алгоритм отрабатывает за одну операцию shuffle, и размер передаваемых по сети данных уменьшается в два раза. :)
Раскладываем эго подграф в памяти
Важным вопросом, который мы пока не рассмотрели, является то, как данные эго подграфа разложить в памяти. Для хранения графа в целом мы использовали список смежности. Эта структура удобна для задач, где необходимо пройти по готовому графу целиком, но затратна, если мы хотим строить граф из кусочков и делать более тонкую аналитику. Идеальная структура для нашей задачи должна эффективно выполнять следующие операции:
- Объединение двух графов, полученных с разных партиций.
- Получение всех друзей человека.
- Проверка факта связаны ли два человека.
- Хранение в памяти без накладных расходов на boxing.
Одним из наиболее подходящих под данные требования форматов является аналог разреженной CSR матрицы:
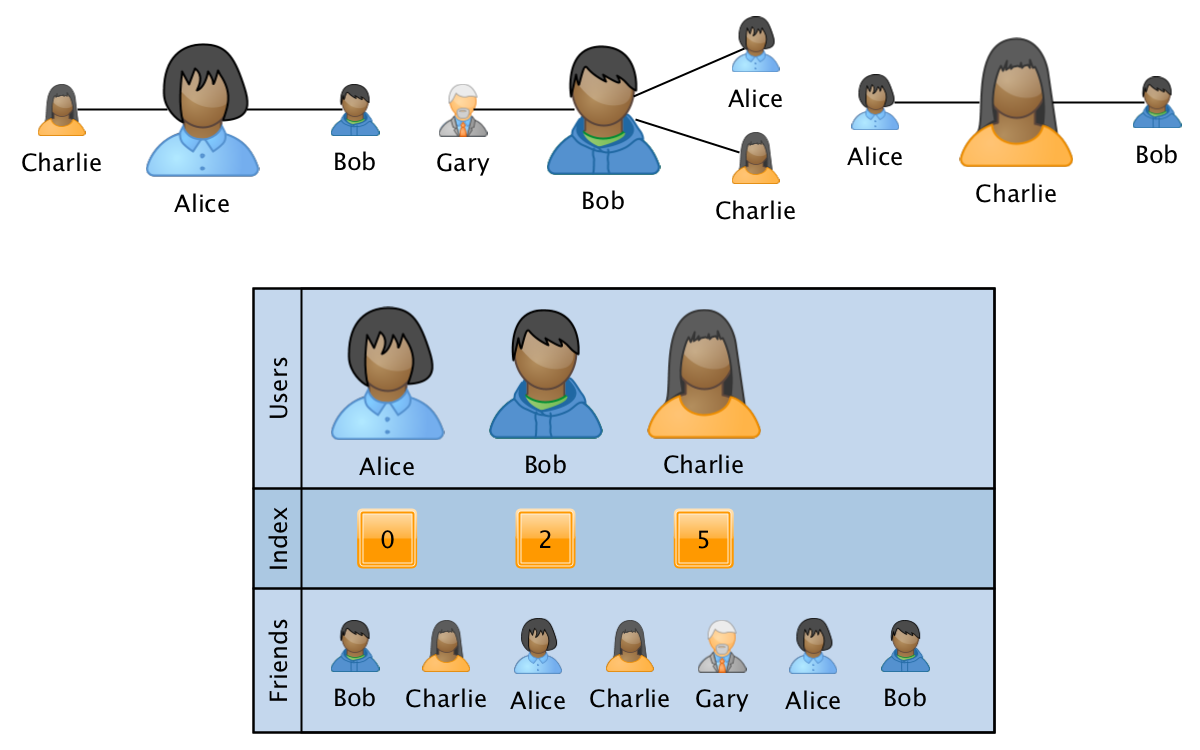
Граф в этом случае хранится в виде трех массивов:
- users — сортированный массив с ID всех участвующих в графе пользователей.
- index — массив того же размера, что и users, где для каждого пользователя хранится индекс-указатель на начало информации о связях пользователя в третьем массиве.
- friends — массив размера, равного количеству ребер в графе, где последовательно указаны ID связанных пользователей для соответствующих ID из users. Для быстроты обработки в пределах информации о связях отдельно взятого пользователя массив отсортирован.
В таком формате операция слияния двух графов выполняется за линейное время, а операции получения информации по конкретному пользователю или по паре пользователей за логарифм от числа вершин. При этом накладные расходы в памяти от размера графа не зависят, так как используется фиксированное число массивов. Добавив четвертый массив data размера, равного размеру friends, можно сохранить и дополнительную информацию, ассоциированную со связями в графе.
Используя свойство симметричности графа, можно хранить только половину дуг "верхнетреугольной формы" (когда дуги хранятся только от меньшего ID к большему), но в этом случае реконструкция всех связей отдельно взятого пользователя будет занимать линейное время. Хорошим компромисом в данном случае может быть подход, использующий "верхнетреугольное" кодирование для хранения и пересылки между узлами, а симметричное кодирование при загрузке эго подграфа в память для анализа.
Уменьшаем shuffle
Однако даже после реализации всех упомянутых выше оптимизации задача по конструированию всех эго подграфов все равно работает слишком долго. В нашем случае порядка 6 часов с высокой утилизацией кластера. При ближайшем рассмотрении видно, что основным источником сложности по-прежнему является операция shuffle, при этом существенная часть данных, участвующих в shuffle, выкидывается на следующих стадиях. Дело в том, что описанный подход строит полную двухшаговую окрестность для каждого пользователя, тогда как эго подграф является лишь относительно небольшим подмножеством этой окрестности содержащим только внутренние дуги.
Например, если бы обрабатывая прямых соседей Боба — Гарри и Фрэнка — мы знали, что они не являются друзьями друг друга, то уже на первом шаге могли бы отфильтровать такие внешние пути. Но для того чтобы узнать для всех Гари и Френков дружат ли они, придется втянуть граф дружб в память на всех вычислительных узлах или делать удаленные вызовы при обработке каждой записи, что, по условиям задачи, невозможно.
Тем не менее, решение есть, если мы позволим себе в небольшом проценте случаев ошибаться находя дружбу там, где её на самом деле нет. Существует целое семейство вероятностных структур данных, позволяющий на порядки сократить потребление памяти при хранении данных, допуская при этом некоторую долю погрешности. Наиболее известной структурой такого рода является фильтр Блума, который уже много лет с успехом применяется в промышленных базах данных для компенсации промахов кэша на "длинном хвосте".
Основная задача фильтра Блума — отвечать на вопрос "входит ли данный элемент в множество ранее виденных элементов?" При этом если фильтр отвечает "нет", то значит элемент наверняка в множество не входит, а вот если он отвечает "да" — есть небольшая вероятность, что элемента там все-таки нет.
В нашем случае "элементом" будет пара пользователей, а "множеством" — все ребра графа. Тогда фильтр Блума можно с успехом применить для сокращения размера shuffle:
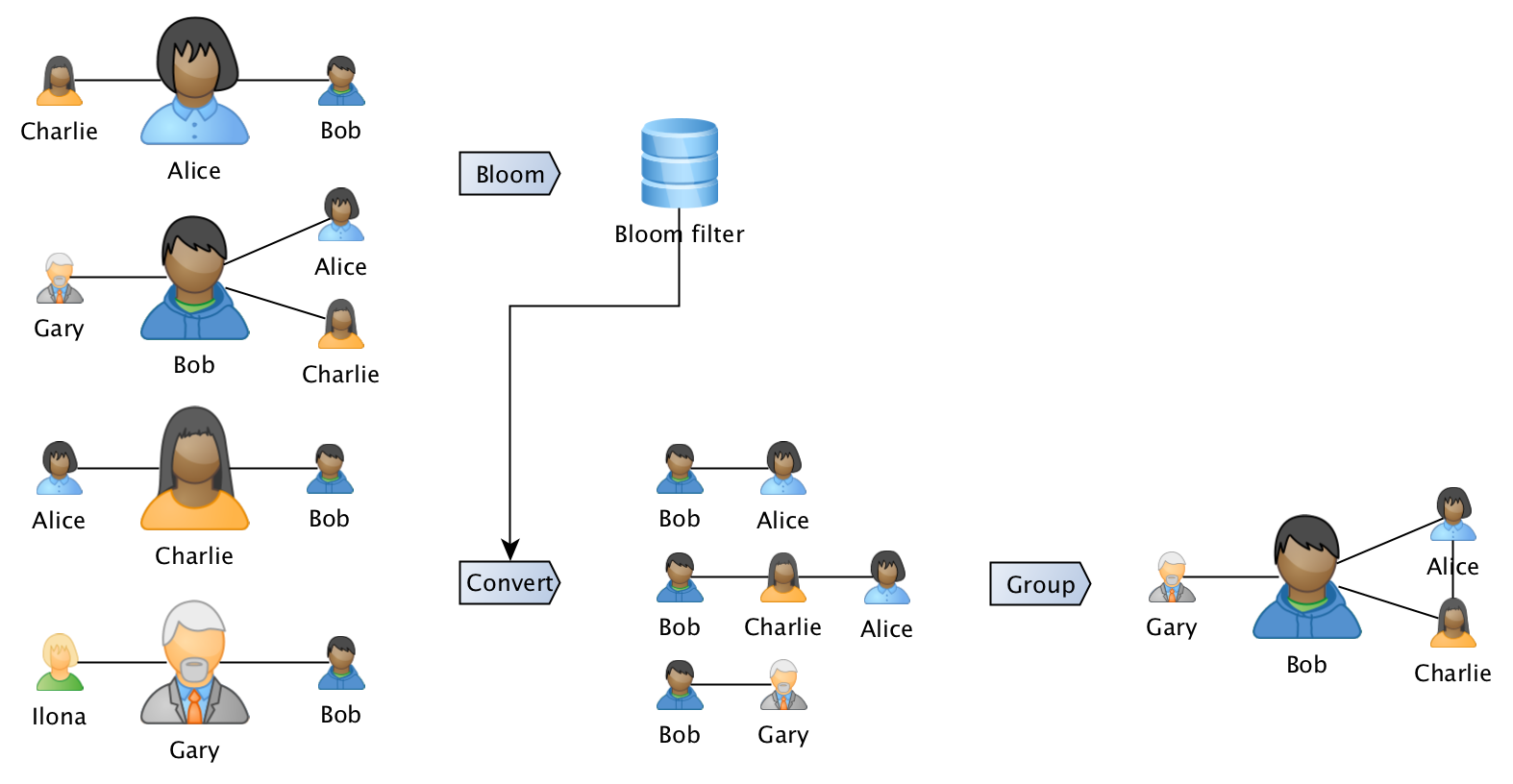
Заранее подготовив фильтр Блума с информацией о графе мы можем просматривая друзей Гарри узнать, что Боб и Илона друзьями не являются, а это значит, что слать информацию о связи Гари и Илоны бобу не нужно. Однако информацию о том, что Гарри и Боб дружат сами по себе, отправить все-таки придется, чтобы Боб мог полноценно восстановить свой граф дружб после группировки.
Убираем shuffle
После применения фильтра количество пересылаемых данных сокращается примерно на 80 %, и задача отрабатывает за 1 час с умеренной загрузкой кластера, позволяющей свободно выполнять другие задачи параллельно. В таком режиме её уже можно принимать "в эксплуатацию" и ставить на ежедневный расчет, но потенциал по оптимизации на самом деле еще есть.
Как бы парадоксально это ни звучало, но задачу можно решить и не прибегая к shuffle, если позволить себе некоторый процент ошибок. И в этом нам может помочь все тот же фильтр Блума:

Если просматривая список друзей Боба с помощью фильтра мы узнаем о том, что Алиса и Чарли почти наверняка являются друзьями, мы можем сразу добавить соответствующую дугу в эго подграф Боба. Весь процесс в этом случае займет меньше 15 минут и не потребует передачи данных по сети, однако некоторый процент дуг, зависящий от настроек фильтра, может оказаться отсутствующим в реальности.
Лишние дуги, добавленные фильтром, для некоторых задач не вносят значимых искажений: например, при подсчете треугольников мы можем легко откорректировать итог, а при подготовке признаков для алгоритмов машинного обучения нужную "корректировку" сможет выучить сам ML-алгоритм на следующем шаге.
Но в некоторых задачах лишние дуги приводят к фатальному ухудшению качества результат: например, при поиске компонент связности в эго подграфе с удаленным эго (без вершины самого пользователя) вероятность появления "фантомного моста" между компонентами растет квадратично относительно их размера, что приводит к тому, что почти везде мы получаем одну большую компоненту.
Есть и промежуточная область, когда негативный эффект от лишних дуг нужно оценивать экспериментально: например, некоторые алгоритмы поиска сообществ могут достаточно успешно справится с небольшим шумом, возвращая практически идентичную структуру сообществ.
Вместо заключения
Эго подграфы пользователей являются важным источником информации, активно используемым в OK для улучшения качества рекомендаций, уточнения демографии, борьбы со спамом, но их вычисление сопряжено с рядом сложностей.
В статье мы рассмотрели эволюцию подхода к задаче построения эго подграфов для всех пользователей социальной сети и смогли улучшить время работы с изначальных 20 часов до 1 часа, а в случае допуска небольшого процента ошибок и до 10-15 минут.
Тремя "китами", на которых основано финальное решение, являются:
- Использование свойства симметричности графа и алгоритмов Tomas Schank.
- Эффективное хранение эго подграфов с помощью разреженной CSR матрицы.
- Применение фильтра Блума для сокращения передачи данных по сети.
Примеры того, как эволюционировал код алгоритма, можно найти в Zeppelin-тетрадке.
Автор: dmitrybugaychenko