Фантастические трюки на языке C

Доброго времени суток, господа и дамы! Иногда у некоторых людей возникает желание заняться откровенным непотребством в программировании — то, что не несет практической пользы напрямую, но помогает развлечься. И я — не исключение. В этой статье я хочу рассказать вам о лайфхаках, трюках (магических и не очень), алгоритмах на языке C!

Идея написать эту статью зародилась из моего поста, после него я начал серию статей, которая раскрывала много интересных моментов — от математических алгоритмов и оптимизации до ГПСЧ.

Увидев, что многим понравилась, я решил продолжить данную серию статей. Части независимы друг от друга, в каждой статье я прикладываю бенчмарки и графики.

В этой статье будет еще порция свежих хаков, фанов, трюков, еще больше магии и скорости!

Всех, кто заинтересовался — прошу под кат.

❯ Содержание

Вы можете читать статьи в любом порядке, они независимы друг от друга:

Наступила юбилейная, пятая часть серии статей.

❯ Алгоритм Флетчера‑32

Данный алгоритм позволяет вычислять 32‑битную контрольную сумму. Разработан Джоном Флетчером из Лаборатории Лоуренса Ливермора в конце 1970‑х годов.

Алгоритм включает разделение слова двоичных данных на короткие «блоки» битов и вычисление модульной суммы этих блоков. Процесс:

1. Инициализировать две суммы — sum1 и sum2 — в ноль.

2. Для каждого 16‑битного слова (2 байта) во входных данных:

   • Добавить значение слова к sum1, взяв результат по модулю 65 535.

   • Добавить новое значение sum1 ко второй сумме, взяв результат по модулю 65 535.

3. Окончательная 32‑битная контрольная сумма формируется путем объединения sum2 (наиболее значащих 16 бит) и sum1 (наименее значащих 16 бит). Результат: Result = (sum2 << 16) | sum1.

Среди особенностей можно выделить, что он чувствителен к порядку блоков, а также алгоритм не является криптографически безопасным — он предназначен для проверки целостности данных, а не для проверки подлинности.

Давайте перейдем к самой сишной реализации:

uint32_t fletcher32(const uint16_t* data, size_t len) {
    uint32_t sum1 = 0xffff, sum2 = 0xffff;

    while (len) {
        size_t tlen = len > 360 ? 360 : len;
        len -= tlen;

        do {
            sum1 += *data++;
            sum2 += sum1;
        } while (--tlen);

        sum1 = (sum1 & 0xffff) + (sum1 >> 16);
        sum2 = (sum2 & 0xffff) + (sum2 >> 16);
    }

    sum1 = (sum1 & 0xffff) + (sum1 >> 16);
    sum2 = (sum2 & 0xffff) + (sum2 >> 16);
    return sum2 << 16 | sum1;
}

Алгоритм работает с массивом 16‑битных слов. В основе лежат две аккумулирующие суммы, инициализированные значением 0xffff. На каждом шаге основного цикла к sum1 прибавляется очередное 16‑битное значение из входного массива, а к sum2 прибавляется текущее значение sum1. Это создает зависимость между всеми элементами данных.

Ключевая особенность реализации — обработка данных блоками по 360 элементов. Это предотвращает возможное переполнение при больших объемах данных. После обработки каждого блока выполняется операция модульной редукции: младшие 16 бит складываются со старшими 16 битами, что равно вычислению остатка от деления на 2¹⁶.

После обработки всех данных выполняется финальная редукция сумм, и результат формируется как объединение sum2 (в старших 16 битах) и sum1 (в младших 16 битах). Такой подход обеспечивает хорошее обнаружение различных типов ошибок, включая перестановки соседних слов.

Ниже я предоставил функцию для того, чтобы получать контрольную сумму строки:

uint32_t fletcher32_string(const char* str) {
    size_t len = strlen(str);
    size_t padded_len = (len + 1) / 2;
    uint16_t* data = (uint16_t*)str;
    return fletcher32(data, padded_len);
}

Данный алгоритм в итоге корректно работает и может показывать следующий результат:

Строка: "Fletcher32 checksum test"
Результат: 0x646d915c

❯ ГПСЧ TinyMT32

TinyMT — генератор псевдослучайных чисел, легкий вариант Mersenne Twister (MT). Представлен в 2011 году Муцуо Сайто и Макото Мацумото. Основное преимущество TinyMT32 — маленький размер внутреннего состояния. И так же, как большинство ГПСЧ, он не подходит для криптографии.

Структура tinymt32_t содержит внутреннее состояние генератора в виде массива из четырех 32‑битных целых чисел.

Кроме того, этот ГПСЧ требует сначала инициализации себя, функция tinymt32_init устанавливает начальное состояние на основе переданного seed. Первый элемент состояния инициализируется значением сида, остальные — константами. Затем выполняется 8‑раундная инициализация с обновлением состояния. Операции сдвига и XOR обеспечивают хорошее распространение сида по всему состоянию.

А вот сама функция генерации выполняет одно преобразование состояния и возвращает псевдослучайное число. Сначала вычисляется промежуточное значение x путем комбинации битов из трех элементов состояния с использованием маски 0x7FFFFFFF и операции XOR. Затем это значение сдвигается влево и снова применяется XOR. Далее выполняется циклический сдвиг элементов состояния, где первые три элемента сдвигаются, а последний вычисляется на основе x и предыдущего состояния. Возвращаемым значением становится новый вычисленный элемент state[3].

typedef struct {
    uint32_t state[4];
} tinymt32_t;

void tinymt32_init(tinymt32_t *tmt, uint32_t seed) {
    tmt->state[0] = seed;
    tmt->state[1] = 0x8f7011ee;
    tmt->state[2] = 0xfc78ff1f;
    tmt->state[3] = 0x3793fdff;

    for (int i = 1; i < 8; i++) {
        tmt->state[i & 3] ^= i + 1812433253 *
            (tmt->state[(i-1) & 3] ^ (tmt->state[(i-1) & 3] >> 30));
    }
}

uint32_t tinymt32_generate(tinymt32_t *tmt) {
    uint32_t x = (tmt->state[0] & 0x7fffffff) ^ tmt->state[1] ^ tmt->state[2];
    x ^= x << 1;
    tmt->state[0] = tmt->state[1];
    tmt->state[1] = tmt->state[2];
    tmt->state[2] = tmt->state[3] ^ (x >> 1);
    tmt->state[3] = x;
    return tmt->state[3];
}

Об этом алгоритме можно прочитать на странице RFC 8682.

❯ Хеш‑функция FNV‑1a

Давайте перейдем к теме хеш‑функций. FNV‑1a (Fowler–Noll–Vo) — одна из них. Она не подходит для криптографии, но позволяет быстро вычислять значения и подходит для хеш‑таблиц.

Алгоритм начинается с инициализации хеш‑значения начальным числом 2166136261. Затем для каждого байта входных данных выполняется две операции: операция XOR текущего хеша со значением байта, за которой следует умножение на 16777619.

uint32_t fnv1a_hash(const void *data, size_t len) {
    const uint8_t *bytes = (const uint8_t*)data;
    uint32_t hash = 2166136261u;

    for (size_t i = 0; i < len; i++) {
        hash ^= bytes[i];
        hash *= 16777619u;
    }
    return hash;
}

❯ Bit reversal (переворот битов)

Данная функция выполняет зеркальную перестановку битов в 32‑битном числе (бит 0 меняется местами с битом 31 и т. д.).

В начале алгоритм меняет местами соседние биты: сдвиг вправо четных битов, влево нечетных, а после — объединение. На втором шаге меняются местами соседние пары битов. Аналогичный сдвиг битов и объединение. Третьим этапом меняет местами соседние четверки битов, после идет смена мест между соседними байтами, и последний пятый шаг меняет местами два 16‑битных полуслова. Здесь используется простой сдвиг: старшие 16 бит сдвигаются вправо, младшие — влево, и результаты объединяются.

uint32_t reverse_bits(uint32_t x) {
    x = ((x >> 1) & 0x55555555) | ((x & 0x55555555) << 1);
    x = ((x >> 2) & 0x33333333) | ((x & 0x33333333) << 2);
    x = ((x >> 4) & 0x0F0F0F0F) | ((x & 0x0F0F0F0F) << 4);
    x = ((x >> 8) & 0x00FF00FF) | ((x & 0x00FF00FF) << 8);
    x = (x >> 16) | (x << 16);
    return x;
}

В результате после последовательных перестановок биты полностью меняются порядком на обратный. Алгоритм эффективен и выполняется за O(log n) операций, где n — количество битов.

❯ MicroLCG — ГПСЧ с 8‑битным состоянием

Данный код реализует линейный конгруэнтный генератор (ЛКГ) для генерации псевдослучайных чисел в диапазоне 0–255.

Линейный конгруэнтный генератор (ЛКГ) — это простейший алгоритм генерации последовательности псевдослучайных чисел, основанный на рекуррентной формуле: Xₙ₊₁ = (a * Xₙ + c) mod m

Работает он следующим образом: функция принимает указатель на 8‑битное число state, которое является текущим состоянием генератора. Внутри функция вычисляет новое значение состояния по формуле: новое состояние = 29 * (текущее состояние) + 217. Операции выполняются с использованием арифметики по модулю 256, поскольку тип uint8_t автоматически обрезает результат до младших 8 бит (это эквивалентно взятию по модулю 256).

uint8_t micro_rand(uint8_t *state) {
    *state = 29 * (*state) + 217;
    return *state;
}

❯ ГПСЧ «Mulberry32» (сверхкомпактный)

Генератор обновляет 32‑битное состояние *state прибавлением константы 0x6D2B79F5. Рабочая копия z проходит два раунда перемешивания.

Каждый раунд использует форму z = (z ^ (z >> N)) * (z | 1). Умножение на (z | 1) (всегда нечётное) — биективная операция по модулю 2³², она не теряет энтропию. XOR со сдвигом z ^ (z >> N) вносит нелинейность, распространяя изменения между битами.

После второго раунда применяется выходная функция z ^ (z >> 14). Она улучшает статистику младших битов, выравнивая их случайность со старшими.

uint32_t mulberry32(uint32_t *state) {
    uint32_t z = (*state += 0x6D2B79F5);
    z = (z ^ (z >> 15)) * (z | 1);
    z ^= z + (z ^ (z >> 7)) * (z | 1);
    return z ^ (z >> 14);
}

Вся логика — это цепь необратимых (сложение) и биективных (умножение на нечётное, XOR со сдвигом) операций. Это создаёт хаотичное преобразование одного слова состояния, достаточное для многих практических задач.

❯ ГПСЧ «RanQ1» (Quick 64‑bit)

Всего одно 64‑битное состояние. Три операции XOR‑shift и одно умножение. Самый быстрый ГПСЧ на диком западе.

uint64_t ranq1_state;

uint64_t ranq1() {
    ranq1_state ^= ranq1_state >> 21;
    ranq1_state ^= ranq1_state << 35;
    ranq1_state ^= ranq1_state >> 4;
    return ranq1_state * 2685821657736338717ULL;
}

Этот генератор работает с одним‑единственным числом — 64‑битным состоянием. Каждый раз, когда нужно новое случайное число, он его быстро взбалтывает и преобразует. Сначала он трижды перемешивает своё состояние с помощью операций, похожих на сдвиг и наложение битов (XOR‑shift). Это как быстро перетасовать колоду: сдвинуть часть битов вправо, наложить на себя, потом сдвинуть влево, снова наложить, и ещё раз немного сдвинуть. Эти три быстрые манипуляции ломают простые закономерности в битах.

Вся хитрость в том, что каждая операция (сдвиг, XOR, умножение) — невероятно быстра для процессора.

❯ Потоковый шифр RC4

Давайте рассмотрим потоковый шифр RC4. RC4 (от англ. Rivest cipher 4 или Ron’s code) — потоковый шифр, разработанный в 1987 году Рональдом Ривестом, сотрудником компании RSA Security. Он состоит из двух основных частей: инициализации и генерации псевдослучайного байта.

Потоковый шифр — это симметричный шифр, в котором каждый символ открытого текста преобразуется в символ шифрованного текста в зависимости не только от используемого ключа, но и от его расположения в потоке открытого текста.

typedef struct {
    uint8_t S[256];
    int i, j;
} RC4_ctx;

Структура RC4_ctx хранит внутреннее состояние шифра: массив S из 256 байт для перестановки и два индекса i и j для работы алгоритма. Это состояние необходимо сохранять между генерациями байтов. Предоставлена она выше.

void rc4_init(RC4_ctx *ctx, const uint8_t *key, int key_len) {
    for (int i = 0; i < 256; i++) ctx->S[i] = i;

    int j = 0;
    for (int i = 0; i < 256; i++) {
        j = (j + ctx->S[i] + key[i % key_len]) & 0xFF;
        uint8_t tmp = ctx->S[i];
        ctx->S[i] = ctx->S[j];
        ctx->S[j] = tmp;
    }
    ctx->i = ctx->j = 0;
}

Функция выше инициализирует состояние шифра. Она сначала заполняет массив S последовательными числами от 0 до 255. Затем она выполняет ключевое расписание, перемешивая этот массив с помощью ключа. Для каждого байта массива вычисляется индекс j на основе текущего j, значения S[i] и байта ключа, после чего элементы S[i] и S[j] меняются местами. Это создаёт уникальную начальную перестановку, зависящую от ключа. В конце функция сбрасывает индексы i и j в ноль, переводя шифр в начальное состояние для генерации потока.

uint8_t rc4_byte(RC4_ctx *ctx) {
    ctx->i = (ctx->i + 1) & 0xFF;
    ctx->j = (ctx->j + ctx->S[ctx->i]) & 0xFF;

    uint8_t tmp = ctx->S[ctx->i];
    ctx->S[ctx->i] = ctx->S[ctx->j];
    ctx->S[ctx->j] = tmp;

    return ctx->S[(ctx->S[ctx->i] + ctx->S[ctx->j]) & 0xFF];
}

Функция rc4_byte генерирует один псевдослучайный байт ключевого потока. Она сначала обновляет индексы i и j: увеличивает i на 1, а j — на значение S[i]. Затем снова меняет местами элементы S[i] и S[j]. На выходе функция возвращает байт из массива S, индекс которого вычисляется как сумма значений только что обменянных S[i] и S[j]. Этот байт и является частью ключевого потока, который можно использовать для шифрования путём операции XOR с открытым текстом.

❯ XOR Linked List

Давайте перейдем к классическим структурам данных. Обычный связный список, но хранящийся в одном указателе через XOR. Ключевая идея: если известен один из соседних узлов, можно получить другой, выполнив XOR с полем link.

typedef struct xor_node {
    int value;
    uintptr_t link;
} xor_node;

Узел хранит значение и поле link, которое содержит результат побитового XOR адресов предыдущего и следующего узлов. Используется uintptr_t для безопасного преобразования указателя в число.

void xor_list_add(xor_node *prev, xor_node *node, xor_node *next) {
    node->link = (uintptr_t)prev ^ (uintptr_t)next;
    prev->link ^= (uintptr_t)next ^ (uintptr_t)node;
    next->link ^= (uintptr_t)prev ^ (uintptr_t)node;
}

xor_node* xor_list_next(xor_node *prev, xor_node *current) {
    return (xor_node*)(current->link ^ (uintptr_t)prev);
}

Функция xor_list_add получает три готовых узла: предыдущий, вставляемый и следующий. Связь нового узла формируется как XOR адресов его соседей. Затем корректируются связи существующих соседей. У предыдущего узла в его поле связи адрес старого следующего заменяется адресом нового узла через операцию XOR. И тот же принцип применяется для следующей ноды.

А для получения следующей ноды (xor_list_next) нужны указатели на текущий и предыдущий узел. Если выполнить операцию XOR этого поля с адресом известного предыдущего узла, результатом будет адрес следующего узла, так как операция обращает сама себя.

❯ Бонус: меняем мантиссу числа на инвертированную

Эта функция меняет мантиссу числа на инвертированную, оставляя экспоненту неизменной. Создает «зеркальные» числа с плавающей точкой. Чисто для фана.

float magic_float_trick(float x) {
    union { float f; uint32_t i; } u = {x};
    u.i = (u.i & 0x7F800000) | (~u.i & 0x007FFFFF);
    return u.f;
}

Данный алгоритм берет float, копирует его экспоненту как есть, а дробную часть (мантиссу) меняет на ее битовую инверсию. Знак всегда становится плюсом. Получается число той же величины (порядка), но со странной дробной частью.

❯ Бенчмарки

Не стану изменять традиции, я также написал бенчмарки наших функций:

Math Algorithms Performance (1000000 iterations):
--------------------------------------------
fast_pow:                3.28 ms  ( 0.003 us/call)
fastest_pow:             2.32 ms  ( 0.002 us/call)
fast_mod:                2.36 ms  ( 0.002 us/call)
is_power_of_two:         2.78 ms  ( 0.003 us/call)
jenkins_hash:           60.47 ms  ( 0.060 us/call)
jenkins_mix+final:      60.55 ms  ( 0.061 us/call)
xor_swap:                4.51 ms  ( 0.005 us/call)
div3:                    2.79 ms  ( 0.003 us/call)
isqrt:                  12.40 ms  ( 0.012 us/call)
to_gray:                 2.79 ms  ( 0.003 us/call)
from_gray:               3.25 ms  ( 0.003 us/call)
counting_sort_256:      15.57 ms  ( 1.557 us/call)
next_power_of_two:       2.81 ms  ( 0.003 us/call)
count_trailing_zeros:    3.56 ms  ( 0.004 us/call)
count_trailing_zeros_kernighan:    3.63 ms  ( 0.004 us/call)
fisher_yates_shuffle:    4.27 ms  ( 0.427 us/call)
Q_rsqrt:                3.25 ms  ( 0.003 us/call)
reverse_bits:           2.79 ms  ( 0.003 us/call)
--------------------------------------------

PRNG Performance (10,000,000 iterations):
-----------------------------------------
xorshift64:       30.94 ms  (323.20M numbers/s)
lehmer64:         44.46 ms  (224.92M numbers/s)
xoshiro256pp:     32.52 ms  (307.46M numbers/s)
pcg32:            23.23 ms  (430.55M numbers/s)
wyrand:           36.15 ms  (276.61M numbers/s)
msws32:           35.61 ms  (280.85M numbers/s)
romu_duo:         27.91 ms  (358.27M numbers/s)
sfc32:            89.55 ms  (111.67M numbers/s)
sha1_prng:       526.40 ms  ( 19.00M numbers/s)
tinymt32:         98.71 ms  (101.31M numbers/s)
mulberry32:       27.86 ms  (358.88M numbers/s)
ranq1:            32.54 ms  (307.35M numbers/s)
rc4_byte:         48.96 ms  (204.23M numbers/s)
-----------------------------------------

Hash Algorithms Performance (1000000 iterations):
--------------------------------------------
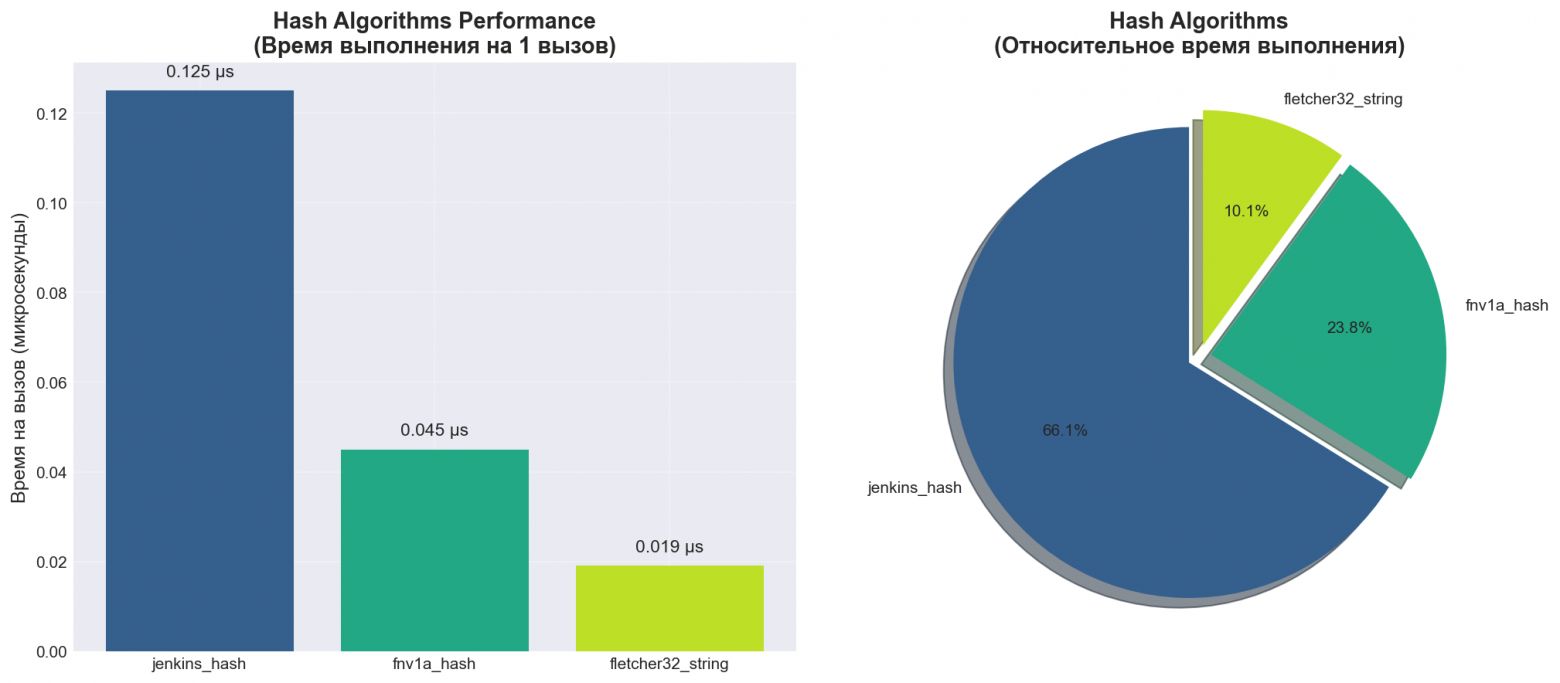
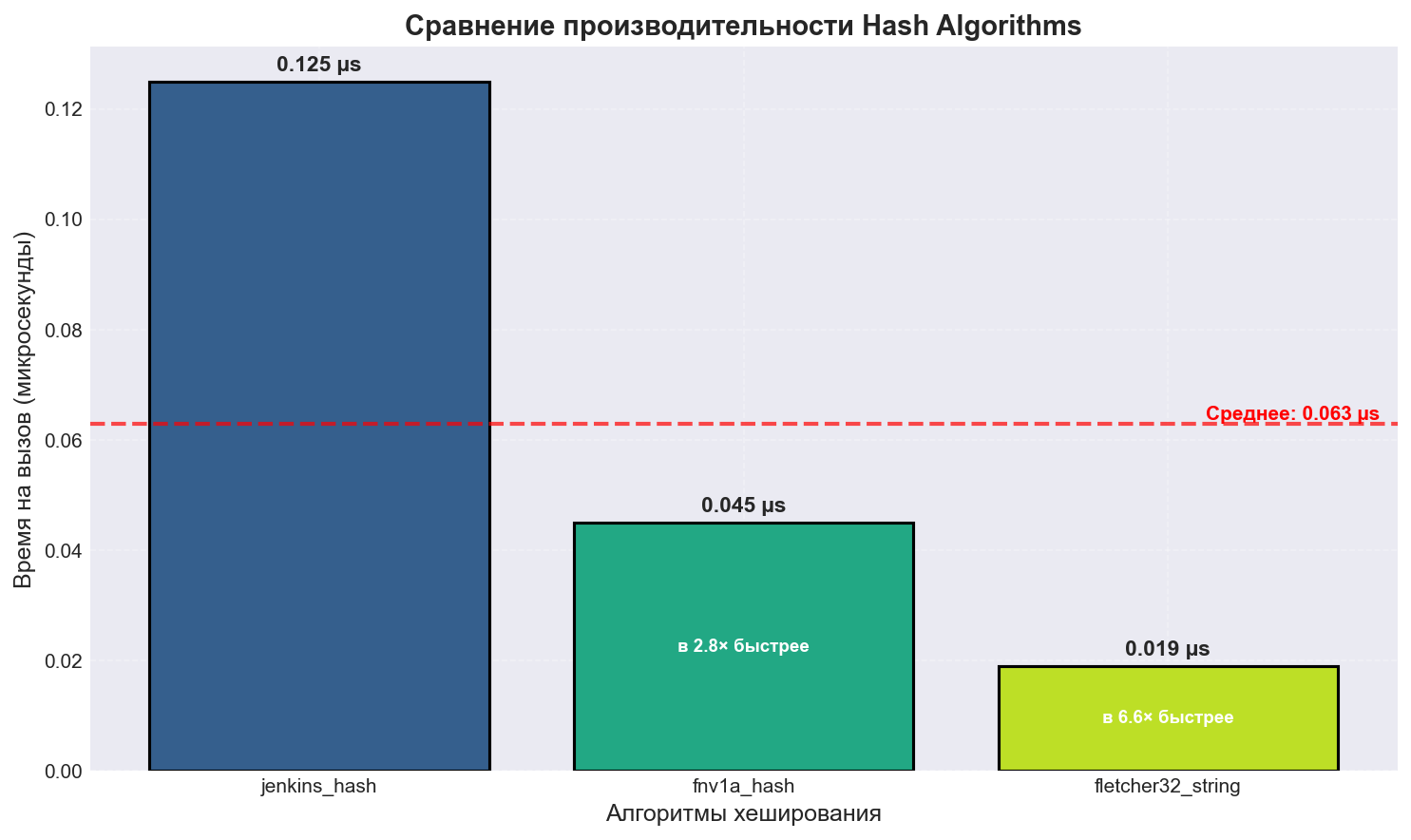
jenkins_hash:          124.68 ms  ( 0.125 us/call)
fnv1a_hash:             45.28 ms  ( 0.045 us/call)
fletcher32_string:      18.81 ms  ( 0.019 us/call)
--------------------------------------------

И также я реализовал графики, чтобы вы визуально могли изучить разницу:

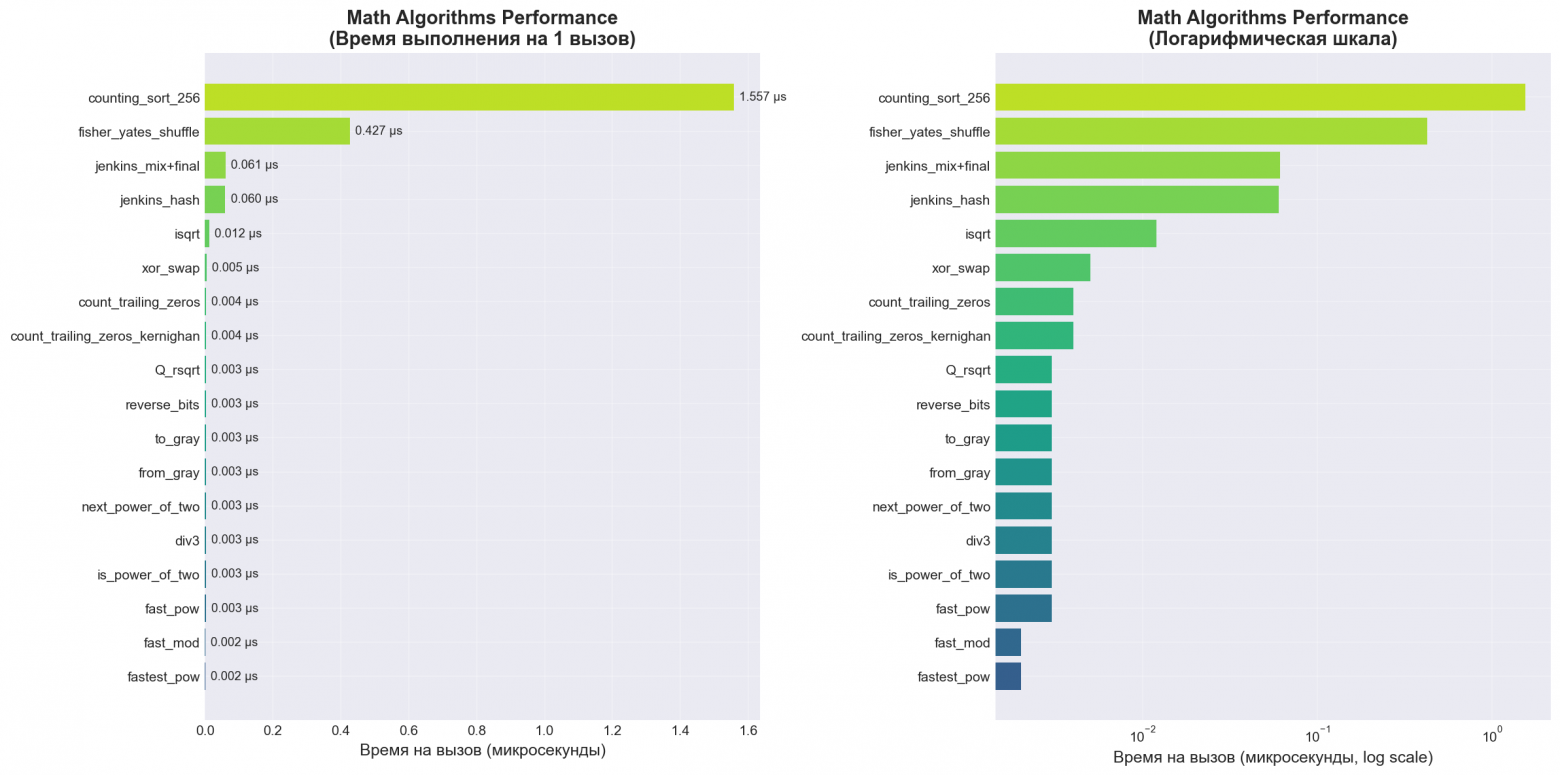
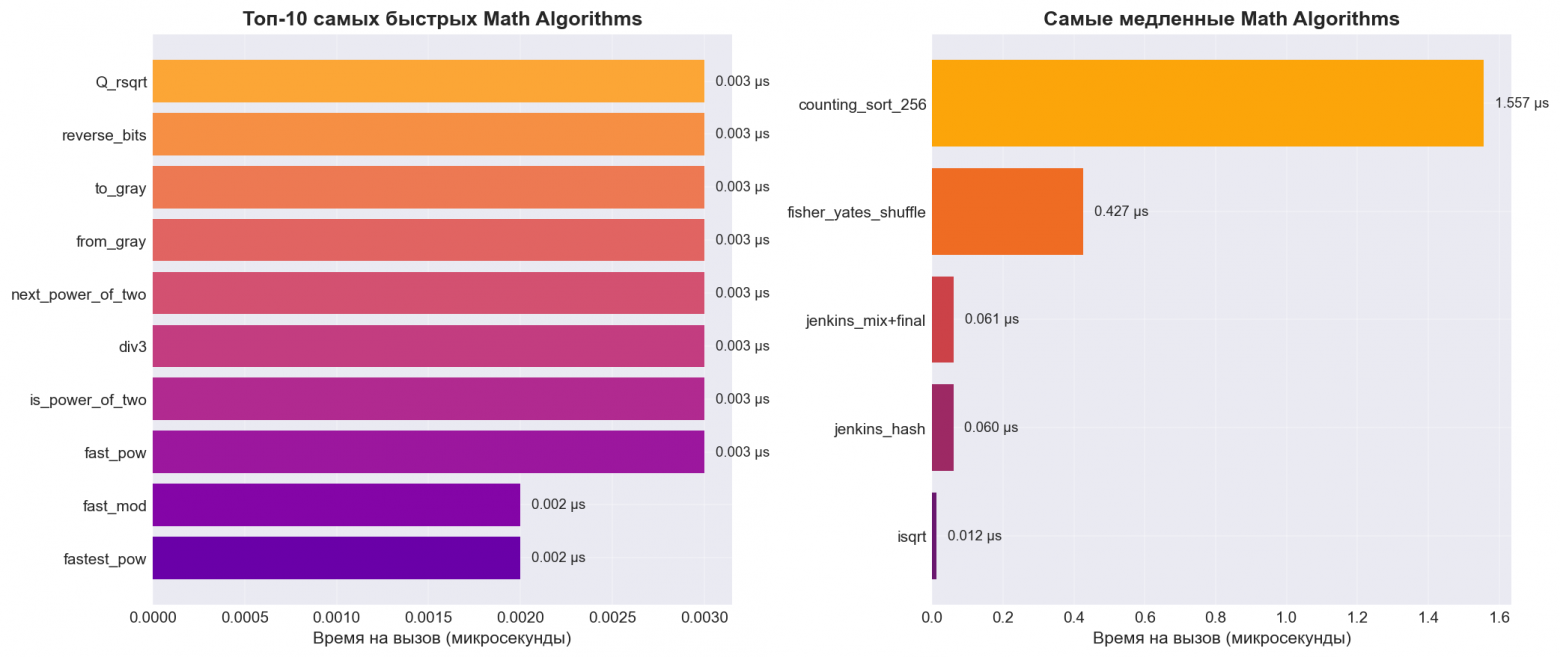
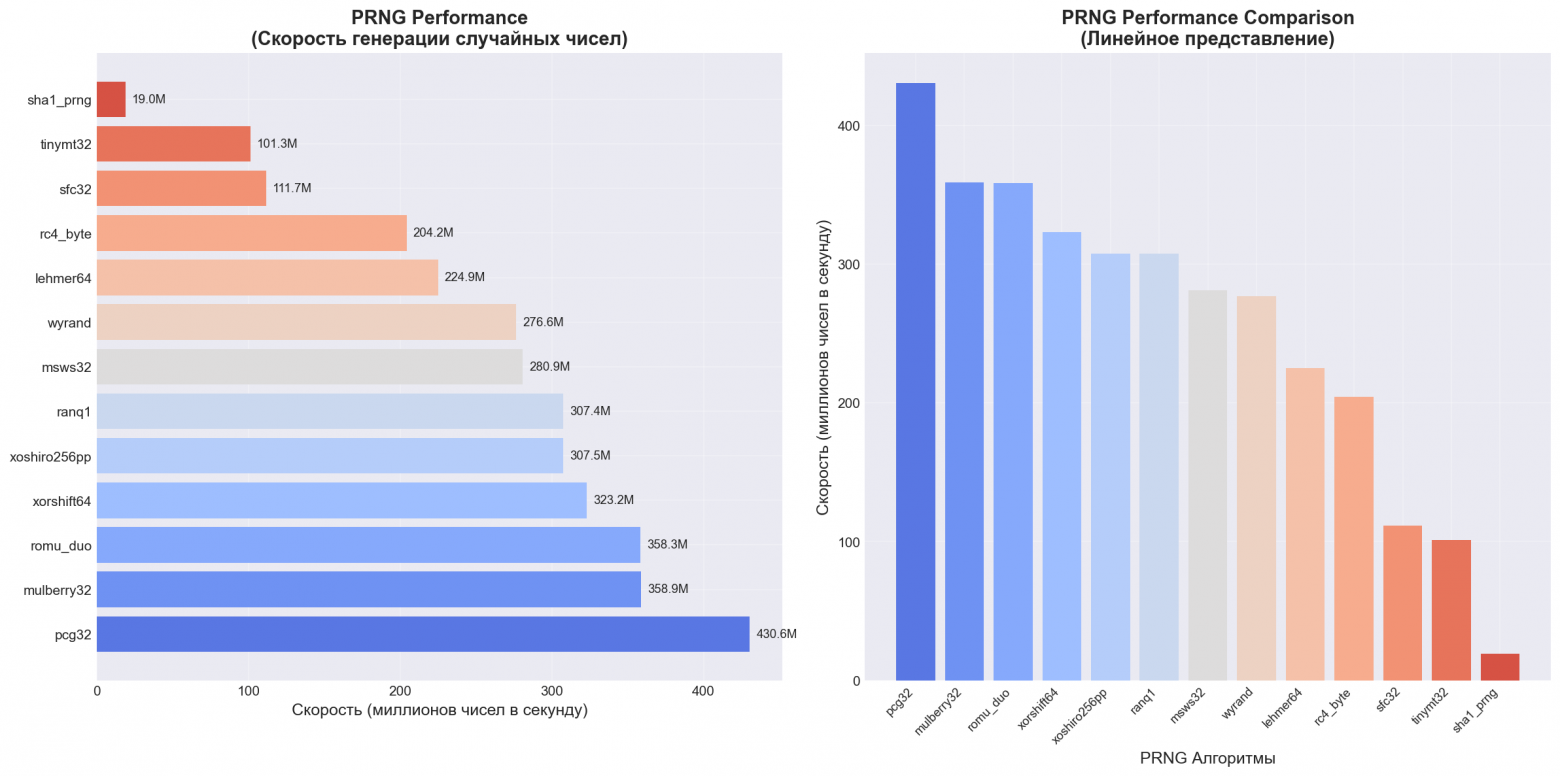
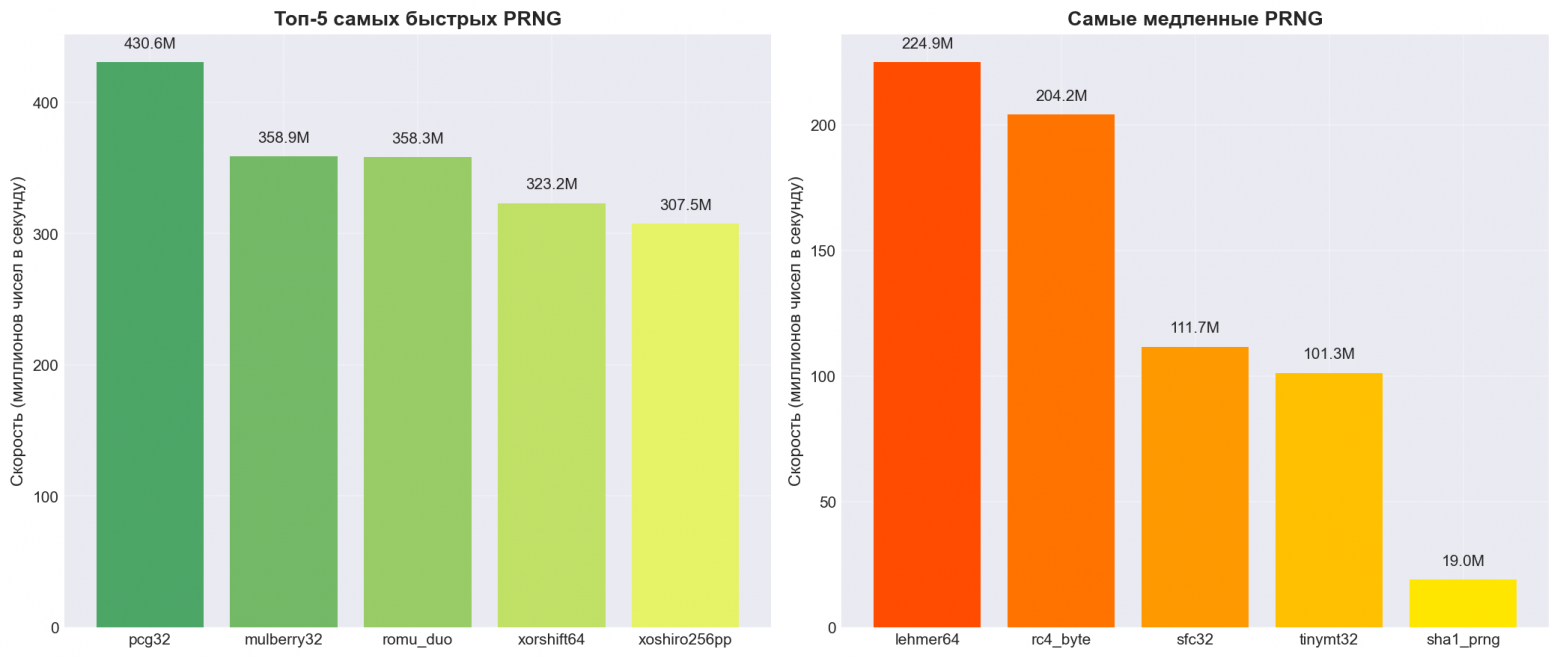
❯ Заключение

Спасибо за прочтение статьи! Я надеюсь, вы узнали что‑то новенькое, или, может, какой‑нибудь трюк натолкнул вас на другой интересный алгоритм. Если нашли нюанс в самой статье — пишите в комментарии.

Если вам понравился изложенный материал, могу предложить вам подписаться на мой блог в телеграме. Если, конечно, вам статья понравилась и вы хотите видеть чуть больше.

Примеры работы кода вы можете увидеть в моем репозитории The Art Of Fun C.