Введение
Всем привет, раз на хабре пошел цикл статей про нейронные сети, то и я напишу про возможность использования нейронных сетей в задаче прогнозирования финансовых временных рядов.
Существует несколько различных теорий о возможности прогнозирования фондовых рынков. Одна из них — гипотеза эффективного рынка, согласно ей, в цене акции уже учтена вся имеющиеся информация и делать прогнозы бессмысленно. Продолжением этой гипотезы можно назвать теорию случайных блужданий.
В теории случайных блужданий информация подразделяется на две категории — предсказуемую, известную и новую, неожиданную. Если предсказуемая, а тем более уже известная информация уже заложена в рыночные цены, то новая неожиданная информация в цене пока еще не присутствует. Одним из свойств непредсказуемой информации является ее случайность и, соответственно, случайность последующего изменения цены. Гипотеза эффективного рынка объясняет изменение цен поступлениями новой неожиданной информации, а теория случайных блужданий дополняет это мнением о случайности изменения цен.
Краткий практический вывод теории случайных блужданий — игрокам рекомендуется использовать в своей работе стратегию «покупай и держи». Следует заметить, что расцвет теории случайных блужданий пришелся на 70-е годы, когда на фондовом рынке США, традиционно являющемся главным полигоном проверки и использования всех новых экономических теорий, не было явных тенденций, а сам рынок находился в узком коридоре. Согласно гипотезе эффективного рынка и теории случайных блужданий прогнозирование цен невозможно. [1]
Однако, большинство участников рынка все же использует различные методы для прогнозирования, предполагая, что сам ряд полон скрытых закономерностей.
Такие скрытые эмпирические закономерности пытался выявить в 30-х годах в серии своих статей основатель технического анализа Эллиот (R.Elliott).
В 80-х годах неожиданную поддержку эта точка зрения нашла в незадолго до этого появившейся теории динамического хаоса. Эта теория построена на противопоставлении хаотичности и стохастичности (случайности). Хаотические ряды только выглядят случайными, но, как детерминированный динамический процесс, вполне допускают краткосрочное прогнозирование. Область возможных предсказаний ограничена по времени горизонтом прогнозирования, но этого может оказаться достаточно для получения реального дохода от предсказаний (Chorafas, 1994). И тот, кто обладает лучшими математическими методами извлечения закономерностей из зашумленных хаотических рядов, может надеяться на большую норму прибыли — за счет своих менее оснащенных собратьев. [2]
Методы прогнозирования
В настоящее время профессиональные участники рынка используют различные методы прогнозирования финансовых временных рядов, основные из них:
1) экспертные методы прогнозирования.
Самый распространенный метод из группы экспертных методов — метод Дельфи. Суть метода заключается в сборе мнений различных экспертов и их обобщение в единую оценку. Если мы прогнозируем этим методом финансовые рынки, то нам нужно выделить экспертную группу людей разбирающихся в этой предметной области (это могут быть аналитики, профессиональные трейдеры, инвесторы, банки итд), провести анкетирование или опрос и сделать обобщение о текущей ситуации на рынке.
2) Методы логического моделирования.
Основаны на поиске и выявлении закономерностей рынка в долгосрочной перспективе.
Сюда входят методы:
— метод сценариев («если — то»), описание последовательностей исходов из того или иного события, с созданием базы знаний;
— методы прогнозов по образу;
— метод аналогий.
3) Экономико-математические методы.
Методы из этой группы базируются на создании моделей исследуемого объекта. Экономико-математическая модель — это определенная схема, путь развития рынка ценных бумаг при заданных условиях. При прогнозировании финансовых временных рядов используют статистические, динамические, микро- макро-, линейные, нелинейные, глобальные, локальные, отраслевые, оптимизационные, дескриптивные. Очень значимы для финансовых наук оптимизационные модели, они представляют из себя систему уравнений, куда входят различные ограничения, а также особое уравнение называемое функционалом оптимальности (или критерием оптимальности). С помощью него находят оптимальное, наилучшее решение по какому-либо показателю.
4) Статистические методы.
Статистические методы прогнозирования применительно, для финансовых временных рядов основаны на построении различных индексов (диффузный, смешанный), расчет значений дисперсии, мат ожидания, вариации, ковариации, интерполяции, экстраполяции.
5) Технический анализ.
Прогнозирование изменений цен в будущем на основе анализа изменений цен в прошлом. В его основе лежит анализ временны́х рядов цен — «чартов» (от англ. chart). Помимо ценовых рядов, в техническом анализе используется информация об объёмах торгов и другие статистические данные. Наиболее часто методы технического анализа используются для анализа цен, изменяющихся свободно, например, на биржах. В техническом анализе множество инструментов и методов, но все они основаны на одном предположении: из анализа временны́х рядов, выделяя тренды, можно спрогнозировать поведение цен.
6) Фундаментальный анализ.
Метод прогнозирования рыночной (биржевой) стоимости компании, основанных на анализе финансовых и производственных показателей её деятельности.
Фундаментальный анализ используется инвесторами для оценки стоимости компании (или её акций), которая отражает состояние дел в компании, рентабельность её деятельности. При этом анализу подвергаются финансовые показатели компании: выручка, EBITDA (Earnings Before Interests Tax, Deprecation and Amortization), чистая прибыль, чистая стоимость компании, обязательства, денежный поток, величина выплачиваемых дивидендов и производственные показатели компании.
[3] [4] [5]
Использование нейронных сетей для прогнозирование финансовых временных рядов
Нейронные сети можно отнести к методам технического анализа, т.к они тоже пытаются выявить закономерности в развитие ряда, обучаясь на его исторических данных.
Финансовый временной ряд довольно сильно зашумлен и поэтому надо уделить особое внимание предобработке данных и кодированию переменных.
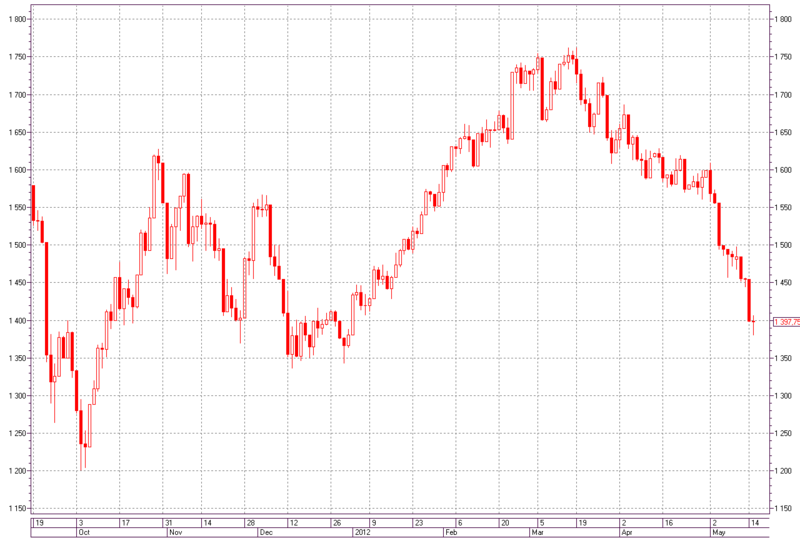
Рис. 1 — Интервальный график в виде японских свечей индекса РТС. Период — день.
Для справки: каждая фигура на графике показывает нам определенный промежуток времени (в данном случае один день) и движения цены за этот промежуток. Опишем их:
— цена открытия — это величина цены в начале этого промежутка времени
— цена закрытия — это величина цены в конце этого промежутка времени
— максимальная цена — это максимальная цена за весь этот промежуток времени
— минимальная цена — это минимальная цена за весь этот промежуток времени
— если цена шла вверх (бычий тренд) за этот период — тело свечи будет белым (или прозрачным)
— если цена шла вниз (медвежий тренд) за этот период — тело свечи будет черным (или закрашенным) [6]
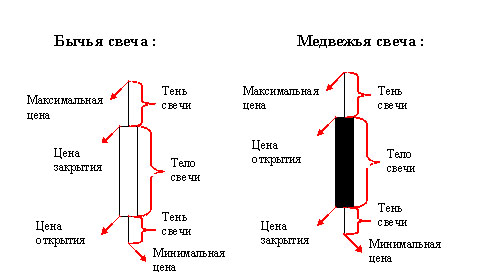
Рис. 2 — Японские свечи.
Действительно значимыми для предсказаний являются изменения котировок. Поэтому на вход нейронной сети после предварительной обработки будем подавать ряд процентных приращений котировок, рассчитанных по формуле X[t] / X[t-1], где X[t] и X[t-1] цены закрытия периодов.
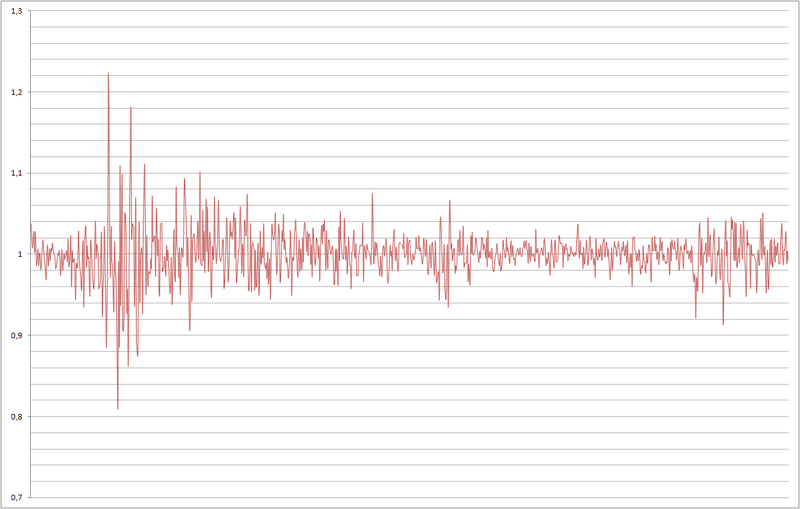
Рис. 3 — Ряд процентных приращений котировок, рассчитанных по формуле X[t] / X[t-1].
Но, т.к. изначально процентные приращения имеют гауссово распределение, а из всех статистических функций распределения, определенных на конечном интервале, максимальной энтропией обладает равномерное распределение, то для этого перекодируем входные переменные, что бы все примеры в обучающей выборке несли примерно одинаковую информационную нагрузку.

Рис. 4 — Распределение процентных приращений котировок.
Алгоритм здесь следующий — отрезок от минимального процентного приращения до максимального разбивается на N отрезков, так, что бы в диапазон значений каждого отрезка входило равное количество процентных приращений котировок.

Рис. 5 — Границы 6 отрезков, количество процентных приращений в каждом отрезке равно.
Далее перекодируем процентные приращения в классы, идентифицирующие каждый отрезок.
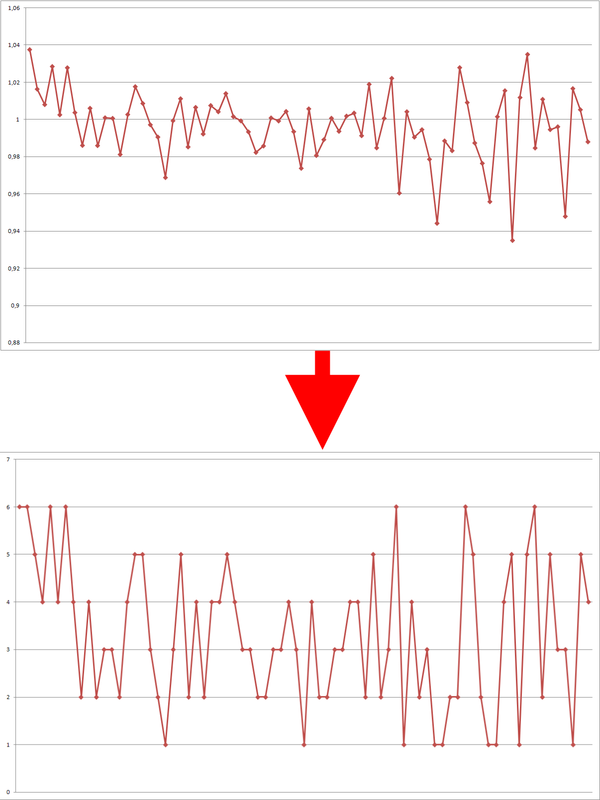
Рис. 6 — Перекодирование процентных приращений.
И получим равномерное распределение.
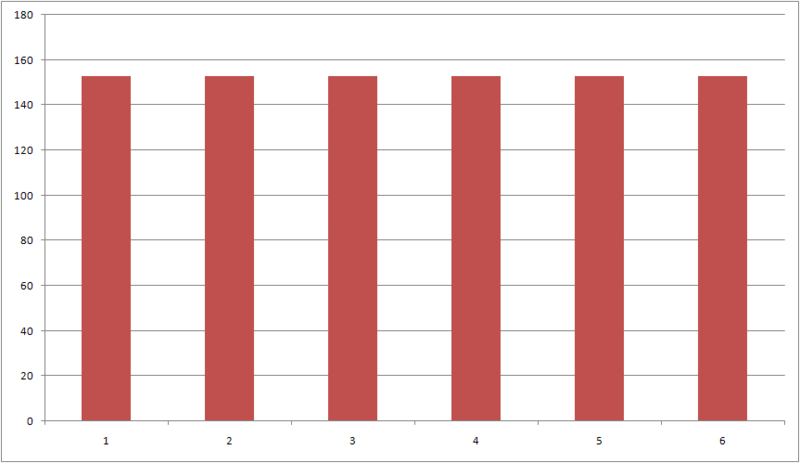
Рис. 7 — Равномерное распределение.
Задача получения входных образов для формирования обучающего множества в задачах прогнозирования временных рядов предполагает использование метода «окна». Этот метод подразумевает использование «окна» с фиксированным размером, способного перемещаться по временной последовательности исторических данных, начиная с первого элемента, и предназначены для доступа к данным временного ряда, причем «окно» размером N, получив такие данные, передает на вход нейронной сети элементы с 1 по N-1, а N-ый элемент используется в качестве выхода.
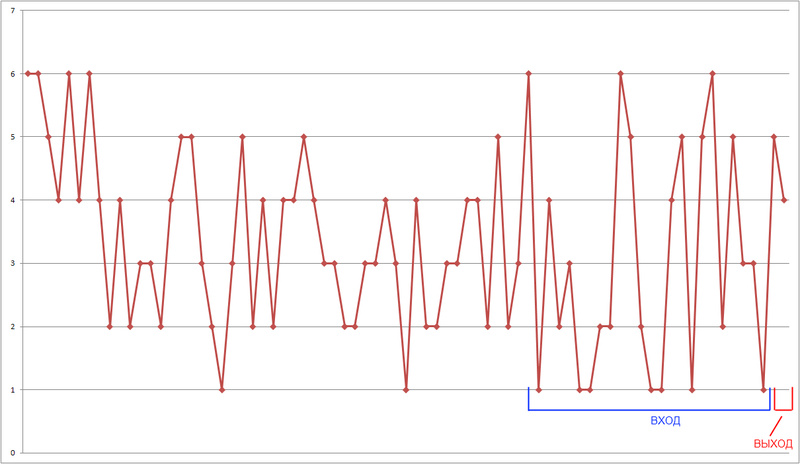
Рис. 8 — Метод «окна».
Качество обучающей выборки тем выше, чем меньше ее противоречивость и больше повторяемость. Для задач прогнозирования финансовых временных рядов высокая противоречивость обучающей выборки является признаком того, что способ описания выбран неудачно. Факторы влияющие на противоречивость и повторяемость:
1) количество элементов обучающей выборки — чем больше элементов, тем больше противоречивость и повторяемость;
2) количество классов на которые перекодировали процентные приращения — при увеличение снижается противоречивость и повторяемость;
3) глубина погружения в финансовый временной ряд («окно») — чем больше глубина, тем меньше противоречивость и меньше повторяемость.
При создании обучающей выборки, меняя эти параметры, необходимо найти баланс при котором уровень противоречивости минимален а повторяемость максимальна.
Для практического примера спрогнозируем направления приращений индекса РТС с 16.01.2012 по 17.04.2012 гг, период — день.
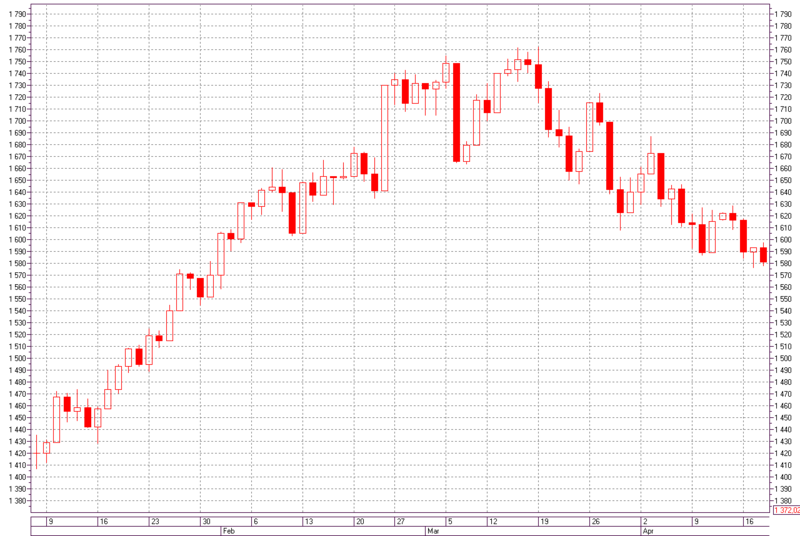
Рис. 9 — График индекса РТС с 8.01.2012 по 18.04.2012 гг, период — день.
Создадим коллекцию нейронных сетей, показавших наилучшие результаты (более 70% правильно спрогнозированных направлений изменений значения индекса) на тестовом множестве (последние 50 периодов). Через каждые 5 периодов коллекция пересоздается, в тестовое множество включается уже прогнозированные периоды. Нейронные сети, входящие в коллекцию не однотипны — у каждой подбирается размер обучающей выборки, количество классов на которые перекодируются процентные приращения, глубина погружения («окно») и количество нейронов в скрытом слое так, что бы наиболее точно прогнозировала текущую рыночную ситуацию (последние 50 периодов).
Базовая архитектура используемых нейронных сетей — многослойный перцептрон с одним скрытым слоем. Есть прекрасная готовая реализация в библиотеке ALGLIB [7]. В качестве алгоритма обучения используем L-BFGS алгоритм (limited memory BFGS), квази-Ньютоновский метод с трудоемкостью итерации, линейной по количеству весовых коэффициентов WCount и размеру обучающего множества, и умеренными требованиями к дополнительной памяти — O(WCount).
Пример коллекции:
Прогноз с: 16.01.2012 по: 20.01.2012
Количество сетей: 16
Параметры сетей:
Вход: 3 Скрытый слой: 18 Количество классов: 4 Длина обучающей выборки: 200 Результат на об. выб.: 74,6 Результат на тестовой выб.: 72,5
Вход: 3 Скрытый слой: 19 Количество классов: 4 Длина обучающей выборки: 200 Результат на об. выб.: 74,6 Результат на тестовой выб.: 72,5
Вход: 3 Скрытый слой: 20 Количество классов: 4 Длина обучающей выборки: 200 Результат на об. выб.: 74,6 Результат на тестовой выб.: 72,5
Вход: 4 Скрытый слой: 18 Количество классов: 4 Длина обучающей выборки: 200 Результат на об. выб.: 75,6 Результат на тестовой выб.: 74,5
Вход: 4 Скрытый слой: 20 Количество классов: 4 Длина обучающей выборки: 200 Результат на об. выб.: 74,1 Результат на тестовой выб.: 72,5
Вход: 5 Скрытый слой: 19 Количество классов: 4 Длина обучающей выборки: 200 Результат на об. выб.: 74,6 Результат на тестовой выб.: 70,6
Вход: 5 Скрытый слой: 20 Количество классов: 4 Длина обучающей выборки: 200 Результат на об. выб.: 76,1 Результат на тестовой выб.: 72,5
Вход: 4 Скрытый слой: 18 Количество классов: 5 Длина обучающей выборки: 200 Результат на об. выб.: 67,2 Результат на тестовой выб.: 74,5
Вход: 5 Скрытый слой: 18 Количество классов: 5 Длина обучающей выборки: 200 Результат на об. выб.: 70,6 Результат на тестовой выб.: 74,5
Вход: 5 Скрытый слой: 19 Количество классов: 5 Длина обучающей выборки: 200 Результат на об. выб.: 76,6 Результат на тестовой выб.: 74,5
Вход: 5 Скрытый слой: 20 Количество классов: 5 Длина обучающей выборки: 200 Результат на об. выб.: 76,1 Результат на тестовой выб.: 74,5
Вход: 3 Скрытый слой: 18 Количество классов: 4 Длина обучающей выборки: 270 Результат на об. выб.: 74,9 Результат на тестовой выб.: 70,6
Вход: 3 Скрытый слой: 19 Количество классов: 4 Длина обучающей выборки: 270 Результат на об. выб.: 74,9 Результат на тестовой выб.: 70,6
Вход: 3 Скрытый слой: 20 Количество классов: 4 Длина обучающей выборки: 270 Результат на об. выб.: 74,9 Результат на тестовой выб.: 70,6
Вход: 5 Скрытый слой: 18 Количество классов: 4 Длина обучающей выборки: 340 Результат на об. выб.: 78,0 Результат на тестовой выб.: 70,6
Вход: 5 Скрытый слой: 19 Количество классов: 4 Длина обучающей выборки: 340 Результат на об. выб.: 79,5 Результат на тестовой выб.: 74,5
Параметры всех использованных коллекций можно посмотреть в файле
Так как прогнозируем направление изменения индекса РТС, то используем простейшую стратегию — открываем позицию по цене закрытия текущего периода и закрываем ее по цене закрытия прогнозируемого периода, фиксируя прибыль или убыток.
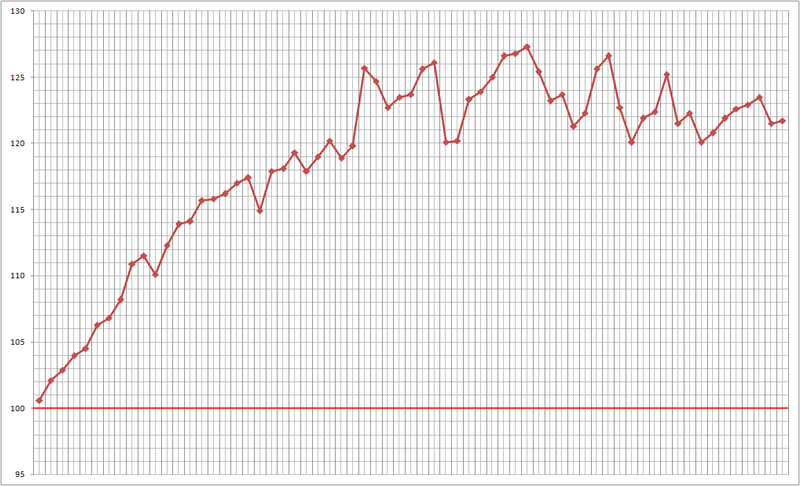
Рис. 10 — Результат работы.
Результат работы с 16.01.2012 по 17.04.2012 гг: 77% правильно прогнозированных направлений изменений значения индекса.
Автор: AzatArslanov

