Проблема кратчайшей общей надстроки формулируется следующим образом: найти кратчайшую строку, такую, что каждая строка из заданного набора являлась бы её подстрокой. Эта проблема имеет место как в биоинформатике (задача сборки генома в общем случае) так и в сжатии данных (вместо данных хранить их надстроку и последовательность пар, вида (индекс вхождения, длина)).
Когда я искал в сети информацию по этой проблеме и её решению на русском языке — находилась лишь пара постов про биоинформатике, где вскользь упоминаются эти слова. Кода (кроме жадного алгоритма), конечно же, тоже не было. Разобравшись в проблеме, этот факт сподвиг на статью здесь.
Осторожно, 4 мегабайта!
По большей части, статья — попытка перевести на понятный язык, проиллюстрировать, приправить примером, и, конечно же, реализовать на Java 4-приближённый алгоритм конструирования надстроки из книжки Дэна Гасфилда (см. использованную литературу). Но сначала небольшое введение и 2-приближенный, жадный алгоритм.
В простейшем случае (если бы в названии проблемы не было слова “кратчайшей”) решением задачи будет простое конкатенирование входных строк в произвольном порядке. Но при данной постановке проблемы мы имеем дело с NP-полнотой, что означает, что в настоящее время не существует алгоритма, с помощью которого можно было бы решить эту задачу на машине Тьюринга за время, не превосходящее полинома от размера данных.
Ввод: S1, S2, …, Sn — множество строк конечного алфавита E*.
Вывод: X — строка алфавита E* содержащая каждую строку S1..n в качестве подстроки, где длина |X| минимизирована.
Пример. Возьмём множество строк S = {abc, cde, eab}. В случае с конкатенированием длина выходной надстроки будет 9 (X = abccdeeab), что, очевидно, не лучший вариант, так как строки могут иметь суффиксно-префиксное совпадение. Длину этого совпадения мы будем называть overlap. (Выбор английского слова произведён неслучайно, так как конкретного и однозначного перевода на русский язык оно не имеет. В русскоязычной литературе обычно используются термины наложение, пересечение, перекрытие и суффиксно-префиксное совпадение).
Отступление. Понятие overlap является одним из важнейших в процессе реализации алгоритмов конструирования надстрок. Вычисление overlap’a для упорядоченной пары строк (Si, Sj) сводится к нахождению длины максимального совпадения суффикса строки Si с префиксом строки Sj.

Один из способов запрограммировать нахождение overlap’a представлен в следующем листинге.
/*
* Функция вычисляет максимальную длину суффикса строки s1
* совпадающего с префиксом строки s2 (длину наложения s1 на s2)
*/
private static int overlap(String s1, String s2)
{
int s1last = s1.length() - 1;
int s2len = s2.length();
int overlap = 0;
for (int i = s1last, j = 1; i > 0 && j < s2len; i--, j++)
{
String suff = s1.substring(i);
String pref = s2.substring(0, j);
if (suff.equals(pref)) overlap = j;
}
return overlap;
}
Возврат к примеру. Если конкатенировать строки S = {abc, cde, eab} с учётом их overlap’ов, то получим строку X = abcdeab с длинной 7, которая короче предыдущей, но не самая короткая. Самая короткая строка получится при конкатенировании строк с учётом overlap’ов в порядке 3-1-2, тогда результирующая строка X = eabcde будет иметь длину 6. Таким образом, мы свели задачу к нахождению оптимального порядка конкатенирования строк с учётом их overlap’ов.
Ограничение. Все существующие алгоритмы нахождения кратчайших надстрок предполагают, что никакая строка входного набора не является подстрокой какой-либо другой строки. Удаление таких строк может быть произведено, например, с помощью суффиксного дерева и, очевидно, не умаляет общности.
Жадный алгоритм
В этом алгоритме на каждой итерации мы пытаемся найти максимальный overlap двух любых строк и слить их в одну. Мы надеемся, что результат этого алгоритма будет близко приближён к фактически оптимальному.
1. Пока S содержит более одной строки, находим две строки с максимальным overlap’ом и сливаем их в одну (например, ABCD + CDEFG = ABCDEFG).
2. Возвращаем одну оставшуюся в S строку.
Пример реализации этого алгоритма представлен в следующем листинге.
/*
* Функция сливает строки с максимальным наложением до тех пор,
* пока не останется единственная строка (общая надстрока).
*/
public static String createSuperString(ArrayList<String> strings)
{
while (strings.size() > 1)
{
int maxoverlap = 0;
String msi = strings.get(0), msj = strings.get(1);
for (String si : strings)
for (String sj : strings)
{
if (si.equals(sj)) continue;
int curoverlap = overlap(si, sj);
if (curoverlap > maxoverlap)
{
maxoverlap = curoverlap;
msi = si; msj = sj;
}
}
strings.add(merge(msi, msj, maxoverlap));
strings.remove(msi);
strings.remove(msj);
}
return strings.get(0);
}
В этом листинге появилась другая простая функция merge, которая сливает две строки в одну с учётом их overlap’a. Так как последний уже был вычислен, логично просто передать его в качестве параметра.
/*
* Функция сливает строки s1 и s2 на длину len, вычисленную с
* помощью функции overlap(s1, s2)
*/
private static String merge(String s1, String s2, int len)
{
s2 = s2.substring(len);
return s1 + s2;
}
Один пример (худший случай):
● Ввод: S = {«abk», «bkc», «bk+1»}
● Вывод жадного алгоритма: «abkcbk+1» с длиной 4+4k
● Вывод оптимального алгоритма: «abk+1c» с длиной 4+2k
Коэффициент приближения исходя из худшего случая 
4-приближённый алгоритм Блюма-Янга-Ли-Тромпа-Яннакакиса
Вообще говоря, у этого алгоритма нет названия и так, как я, его никто не называет. Называется он просто 4-приближённый алгоритм конструирования кратчайшей надстроки. Но так как его придумали Блюм, Янг, Ли, Тромп и Яннакакис, почему бы не дать такой заголовок?
Для наглядности, во время разбора алгоритма я буду приводить пример построения надстроки для набора S = {S0: “cde”, S1: “abc”, S2: “eab”, S3: “fgh”, S4: “ghf”, S5: “hed”}.
Основной идеей алгоритма является нахождение покрытия циклами минимальной полной длины для полного направленного взвешенного графа, вершинами которого являются строки заданного набора, а вес ребра из Si в Sj равен overlap(Si, Sj) для всех i, j.
Граф для нашего примера (вершины для видимости подписаны i вместо Si):
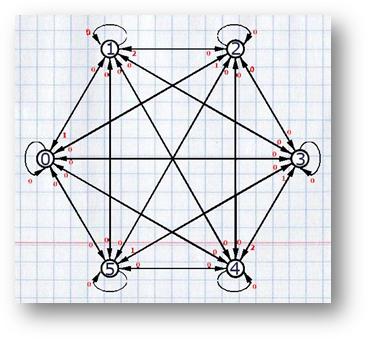
В своей реализации я буду представлять этот граф как матрицу смежности, которая будет формироваться банальным образом, показанном в следующем листинге (в п.16.17 [1] Д. Гасфилд утверждает, что матрицу можно формировать эффективнее, но способ формирования этой матрицы не влияет на рассмотрение данного алгоритма).
int n = strings.size();
// Вычисление матрицы overlap'ов для всех
// упорядоченных пар (Si, Sj).
int[][] overlaps = new int[n][n];
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
overlaps[i][j] = overlap(strings.get(i), strings.get(j));
Для нашего примера матрица смежности будет выглядеть так:
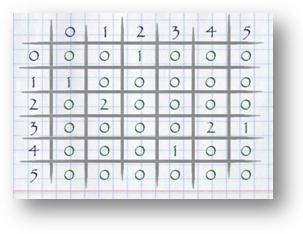
После того, как матрица смежности построена, встаёт необходимость найти покрытие циклами минимальной полной длины. Такое покрытие можно найти, сводя эту задачу к “задаче о назначениях”. Итак, задачей стало найти полное назначение максимального веса (как оказалось, этот шаг алгоритма занимает доминантное время). Быстрее и проще ([1] п.16.19.13) это назначение можно найти жадным методом.
Жадное назначение ([1] п.16.19.13)
Исходные данные: матрица A размером k × k.
Результат: полное назначение M.
- Положить M = Ø и объявить все клетки A доступными.
- while в A есть доступные клетки do begin
- Среди доступных клеток A выбрать клетку (i, j) наибольшего веса.
- Поместить клетку (i, j) в M и сделать клетки в строчке i и столбце j недоступными.
- end;
- Выдать полное назначение M.
Представить M в коде можно в виде массива (int[] M = new int[k]) и первую часть инструкции 2.2 трактовать как M[i] = j; так как в полном назначении каждое число от 0 до k встречается ровно один раз как индекс строки и ровно один раз как индекс столбца.
Пример реализации вычисления полного назначения представлен в следующем листинге.
/*
* Функция, вычисляющая полное назначение максимального
* веса жажным методом. Время - O(k*k*log(k))
*/
private static int[] assignment(int[][] a)
{
int n = a.length;
boolean[][] notallow = new boolean[n][n];
int[] m = new int[n];
while (true)
{
int max = -1, maxi = -1, maxj = -1;
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
if (notallow[i][j]) continue;
if (a[i][j] > max)
{
max = a[i][j];
maxi = i; maxj = j;
}
}
}
if (max == -1) break;
m[maxi] = maxj;
for (int i = 0; i < n; i++)
{
notallow[maxi][i] = true;
notallow[i][maxj] = true;
}
}
return m;
}
Пошаговое вычисление полного назначения максимального веса жадным методом для нашего примера:

Теперь, когда вычислено полное назначение максимального веса, необходимо вычислить покрытие циклами минимальной полной длины. Для этого нужно:
взяв за начало любой (логично – нулевой) индекс полного назначения, положить его в цикл, пометить использованным и посмотреть, равняется ли его значение индексу начала цикла? Если да – закончить цикл, положить его в покрытие циклами и начать новый цикл, взяв за начало первый непомеченный элемент. Если нет – взять это значение за индекс и повторить процедуру, пока все элементы не станут помечены.
Представление покрытия циклами в памяти можно организовать как список списков индексов строк.
Листинг алгоритма (assign – полное назначение):
// Нахождение покрытия циклами минимальной полной длины
// для полного назначения assign
ArrayList<ArrayList<Integer>> cycles
= new ArrayList<ArrayList<Integer>>();
ArrayList<Integer> cycle = new ArrayList<Integer>();
boolean[] mark = new boolean[assign.length];
for (int i = 0; i < assign.length; i++)
{
if (mark[i]) continue;
cycle.add(i);
mark[i] = true;
if (assign[i] == cycle.get(0))
{
cycles.add(cycle);
cycle = new ArrayList<Integer>();
i = 0;
}
else
{
i = assign[i] - 1;
}
}
Для нашего примера нахождение покрытия циклами будет выглядеть следующим образом:
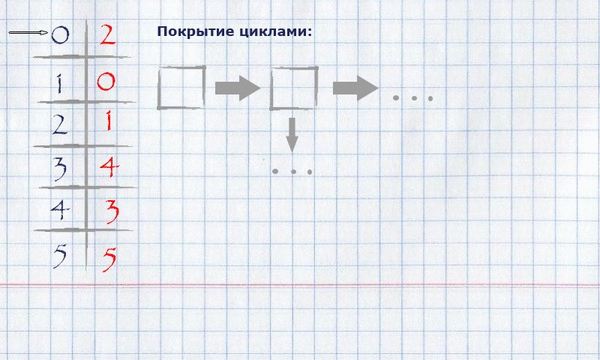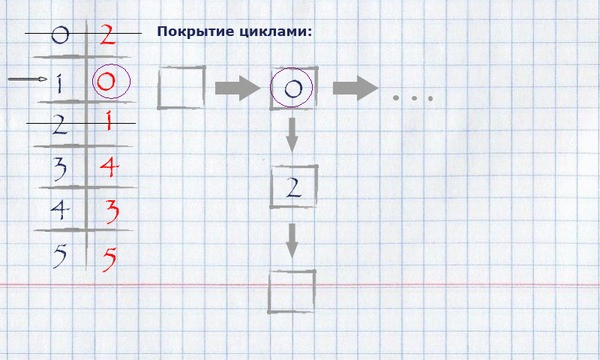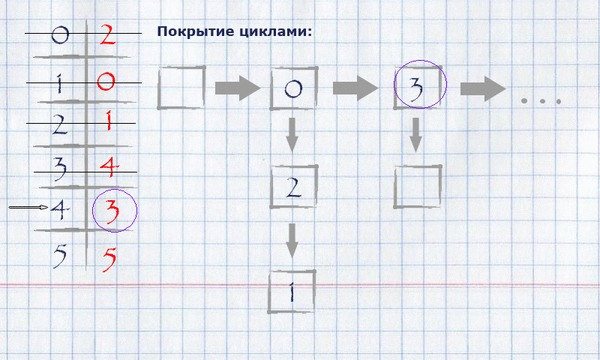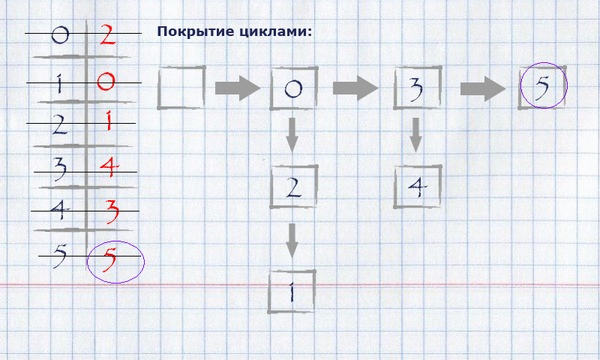
Получившееся покрытие циклами можно отобразить на изначальном графе, оставив на нём только те рёбра, которые попали в покрытие.
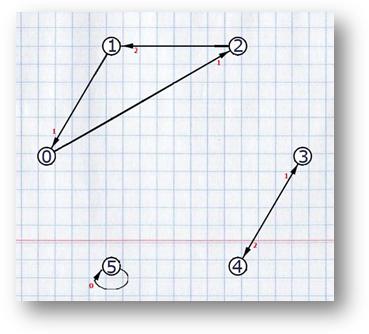
Сборка. Теперь, когда все циклы в покрытии вычислены, можно приступать к сборке, непосредственно, надстроки.
Для этого понадобится функция prefix, которая принимает строки S1 и S2 и возвращает строку S1, обрезанную справа на overlap(S1, S2) символов. Но так как все overlap’ы были нами давно посчитаны, то функцию можно написать так, чтобы она принимала только одну строку и количество символов, на которое её нужно укоротить.
/*
* Функция возвращает строку s1, обрезанную справа
* на ov символов
*/
private static String prefix(String s1, int ov)
{
return s1.substring(0, s1.length() - ov);
}
Теперь для каждого цикла Ci = {S1, S2, …, Sk-1, Sk} необходимо составить надстроку XCi = prefix(S1, overlap(S1, S2)) ++ prefix(S2, overlap(S2, S…)) ++ prefix(S…, overlap(S…, Sk-1)) ++ Sk.
Проблема состоит в том, что, так как циклы в покрытии – это циклы — значит, мы можем их циклически крутить и непонятно, с какой строки начать конструирование надстроки XCi. Ответ оказывается прост – нужно сдвинуть цикл так, чтобы минимизировать overlap последней и первой строки.
Рассмотрим первый цикл циклического покрытия из примера.

Если не минимизировать overlap последней и первой строки, а взять C0 = {1, 0, 2}, то надстрокой будет XC0 = abc ++ cde ++ eab = abcdeab, очевидно, не самая короткая из возможных. Минимальный overlap в этом цикле – 1, значит, нам подойдёт любая из последовательностей {0, 2, 1} (cde ++ eab ++ abc = cdeabc) или {2, 1, 0} (eab ++ abc ++ cde = aebcde).
Далее приведён код, который циклически сдвигает каждый цикл в покрытии так, чтобы минимизировать overlap’ы первых и последних строк каждого цикла, и конструирует надстроки для каждого цикла.
// Циклический сдвиг каждого цикла в покрытии такой, чтобы
// минимизировать overlap первой и последней строки в цикле
// и конструирование надстроки для каждого цикла.
ArrayList<String> superstrings = new ArrayList<String>();
for (ArrayList<Integer> c : cycles)
{
String str = "";
ArrayList<Integer> ovs = new ArrayList<Integer>();
for (int i = 0; i < c.size() - 1; i++)
ovs.add(overlaps[c.get(i)][c.get(i+1)]);
int min = overlaps[c.get(c.size()-1)][c.get(0)];
int shift = 0;
for (int i = 0; i < ovs.size(); i++)
if (ovs.get(i) < min)
{
min = ovs.get(i);
shift = i + 1;
}
Collections.rotate(c, -shift);
for (int i = 0; i < c.size() - 1; i++)
str += prefix(strings.get(c.get(i)),
overlaps[c.get(i)][c.get(i+1)]);
str += strings.get(c.get(c.size()-1));
superstrings.add(str);
}
Теперь у нас есть кратчайшие надстроки для каждого цикла в покрытии. Рассматриваемый алгоритм с множителем 4 предполагает простую конкатенацию этих строк.
// Конкатенация всех надстрок из superstrings
StringBuilder superstring = new StringBuilder();
for (String str : superstrings)
superstring.append(str);
return superstring.toString();
Исходные коды и тестирование
Исходные коды жадного (Greedy.java) и Блюма-Янга-Ли-Тромпа-Яннакакиса (Assign.java) алгоритмов доступны в git-репозитории по ссылке bitbucket.org/andkorsh/scss/src. Также там есть исполняемый класс Main.java, который при запуске запрашивает количество запусков для замера скорости алгоритмов и путь к входному файлу. Также класс Main умеет генерировать входные данные сам, для этого вместо имени файла нужно ввести «random», после чего будет запрошено количество строк, максимальная длина строки, фиксированная длина или нет и количество символов в алфавите. Отчёт запишется в файл output.txt.
Исходные коды гарантированно компилируются javac, начиная с версии “1.6.0_05”.
Тестирование выполняется с помощью функции test класса Main.
private static int test(ArrayList<String> substrings, String superstring)
{
int errors = 0;
for (String substring : substrings)
if (superstring.indexOf(substring) < 0)
errors++;
return errors;
}
Использованная литература
[1]: Дэн Гасфилд. Строки, деревья и последовательности в алгоритмах. Информатика и вычислительная биология. Невский Диалект, БХВ-Петербург, 2003г. – 656 с.: ISBN 5-7940-0103-8, 5-94157-321-9, 0-521-58519-8.
www.ozon.ru/context/detail/id/1393109/
[2]: Dan Gusfield. Algorithms on Strings, Trees and Sequences: Computer Science and Computational Biology. THE PRESS SYNDICATE OF THE UNIVERSITY OF CAMBRIDGE, 1997г. – 534 с.: ISBN-10: 0521585198, ISBN-13: 978-0521585194.
www.amazon.com/Algorithms-Strings-Trees-Sequences-Computational/dp/0521585198
[3]: Shunji Li, Wenzheng Chi. Lecture #3: Shortest Common Superstring – CS 352 (Advanced Algorithms), Spring 2011.
cs.carleton.edu/faculty/dlibenno/old/cs352-spring11/L03-shortest-superstring.pdf
Автор: korshunov
