Христианское учение о Троице — это представление о едином Боге, выступающем в ипостасях Бога-Отца, Бога-Сына и Святого Духа. Доктрина вычислительного тринитаризма состоит в том, что вычисление представляется в трех формах: доказательствах высказываний, программах некоторого типа и отображений между структурами. Каждый из этих аспектов есть объект поклонения одной из трех деноминаций: логики, утверждающей главенство доказательств и высказываний, теории языков программирования, обращающейся в первую очередь к программам и типам, и теории категорий, отдающей первенство отображениям и структурам. Основной догмат вычислительного тринитаризма гласит, что логики, языки программирования и категории — всего лишь манифестации единого божественного понятия вычисления. Не существует наилучшего пути к просветлению, каждый из аспектов даёт возможность понимания того, что в нашей жизни представляет собой опыт вычисления.
Вычислительный тринитаризм имеет следствием, что любая концепция, возникшая в рамках одного из трех подходов, должна также иметь значение с точки зрения двух других. Если же получен результат, существенный и для логики, и для теории типов, и для теории категорий, то можно быть уверенным, что удалось прояснить некоторую существенную сторону понятия вычисления, а значит, совершено подлинное научное открытие. Успехи в нашем понимании вычисления могут происходить из результатов, полученных различными путями (любые данные полезны и уместны), а истинность результатов не зависит от их известности.
Логика говорит о том, какие высказывания существуют (какие виды мыслей мы хотим уметь выразить) и что представляет собой доказательство (как мы можем сообщать наши мысли другим). Языки (в том смысле слова, какой принят в информатике) сообщают, какие существуют типы (какие вычислительные явления мы хотим уметь выразить) и что представляет собой программа (каким образом эти явления возможно осуществить). Категории говорят о том, какие существуют структуры (с какими математическими моделями нам придётся работать) и что представляет собой отображение между ними (как они относятся друг к другу). В этом смысле все три подхода предписывают, чему быть, а не описывают то, что дано заранее. И в том же смысле они представляют собой основания. Если предположить, что они обладают лишь описательной силой, вопрос о происхождении заранее данных концепций останется без ответа, что вновь потребует обращения к проблеме оснований. Здесь я хочу обсудить именно основания, поскольку это поможет, как я надеюсь, исправить некоторые распространённые заблуждения относительно понятий высказывания, типа и структуры. В особенности интересно здесь то, что в рамках рассматриваемой концепции система типов не представляет собой произвольный набор ограничений, налагаемых на данное заранее понятие программы (независимо от того, используются ли при её записи горизонтальные линии или нет). Скорее, система типов — это способ говорить о том, что в первую очередь представляют собой программы и каким образом их можно интерпретировать как доказательства и отображения.
Далее я опишу основные соответствия между логикой, языками программирования и категориями на основе их структурных свойств (и пока этим ограничусь).
Центральная концепция логики — следование, записывающееся в виде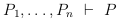 
и выражающее выводимость 
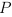из 
. Подобная запись говорит, что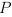 
может быть получено в соответствии с правилам логики, если 
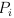даны в качестве аксиом. В отличие от структурного следования (которое здесь обсуждаться не будет), эта форма следования не выражает импликации! В частности, следование из пустого набора аксиом невозможно. Следование обладает по меньшей мере двумя ключевыми структурными свойствами, позволяющими рассматривать его в качестве отношения предпорядка:
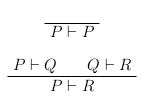
Кроме того, часто вводятся следующие дополнительные структурные свойства:
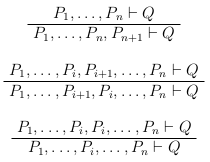
Они говорят о том, что «дополнительные» аксиомы не влияют на выводимость, «переупорядочивание» аксиом не играет роли, «удвоение» аксиом не играет роли. Эти условия кажутся неизбежными, но в так называемых субструктурных логиках любые из этих аксиом могут не иметь места.
В теории языков программирования базовая концепция — суждение о типизации, записывающееся как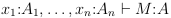 
и утверждающее, что 
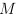есть выражение типа 
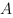, содержащее переменные 
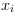типа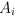 
. Суждение о типизации должно удовлетворять следующим основным структурным свойствам:
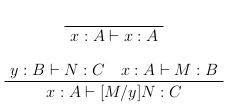
Можно думать о переменных как об именах «библиотек», при этом первое свойство говорит о том, что использоваться может любая библиотека, а второе — о замкнутости относительно компоновки (как в программе ld в Unix и аналогичных), где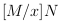 
есть результат компоновки x с библиотекой M в выражении N. Обычно мы ожидаем, что аналоги аксиом «дополнения», «переупорядочивания» и «удвоения» будут выполняться и здесь, хотя это не обязательно. Их формулировка оставляется читателю в качестве упражнения.
В теории категорий основная концепция — концепция отображения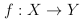 
между структурами X и Y. Простейшими примерами являются, вероятно, множества и функции между ними, однако чаще рассматриваются, например, топологические пространства и непрерывные отображения между ними. Отображение удовлетворяет аналогичным структурным свойствам:
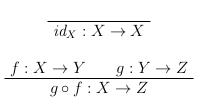
Они выражают существование идентичного отображения и замкнутость отображений относительно композиции. Они соответствуют рефлексивности и транзитивности следования в логике и правилам «подключения библиотеки» и «компоновки» в теории языков программирования. Как и прежде, можно ожидать существования дополнительных условий замкнутости, соответствующих аксиомам «дополнения», «переупорядочивания» и «удвоения», которые можно охарактеризовать с помощью ряда дополнительных требований. Здесь я не буду углубляться в эту тему, так как эти условия подробно рассматриваются во многих стандартных источниках по теории категорий.
Вычислительный тринитаризм пленит меня своей красотой! Представьте себе мир, в котором логика, программирование и математика едины, в котором любому доказательству отвечает программа, любой программе — отображение, любому отображению — доказательство! Представьте себе мир, в котором код — это математика, где нет разделения на рассуждение и осуществление, нет различия между языком математики и языком вычислений. Тринитаризм — это центральный организующий принцип теории вычислений, интегрирующий, объединяющий и обогащающий язык логики, программирования и математики. Он дает средства открытия и анализа вычислительных явлений. Новшество в одной области обязано иметь последствия для остальных. Хорошая идея хороша независимо от того, в какой форме она была впервые сформулирована. Если же какая-то идея не имеет смысла одновременно с логической, теоретико-категорной и теоретико-типовой точки зрения — она не может быть проявлением божественного.
Автор: VtQveant
