При проектировании систем управления технологическими процессами (АСУ ТП) разрабатываются различные виды обеспечения: методическое, информационное, техническое, эргономическое, программное и др., но особую роль среди них занимает математическое обеспечение (далее МО), определяемое как совокупность математических методов, моделей и алгоритмов, используемых при работе автоматизированной системы. Современная АСУ ТП должна быть системой оптимального управления. Она должна обеспечить условия, чтобы его величество технологический процесс чувствовал себя максимально комфортно и мог выдать все, на что он способен. Разработчики МО должны хорошо разбираться в технологическом процессе, который автоматизируется, обладать навыками математического моделирования этих самых процессов в статике и в динамике, а также владеть математическими методами оптимального управления.
Наиболее востребованным продуктом, необходимым человеку, является энергия. Чем дальше мы идем в будущее, тем больше требуется энергии, причем энергии экологически чистой, универсальной и удобной для использования. Этим требованиям в наибольшей степени отвечает электрическая энергия. Особенностью энергетики, в отличие от других отраслей экономики, является невозможность хранения ее готового продукта в достаточном количестве, поэтому в рамках энергосистемы электроэнергии должно вырабатываться столько, сколько требуется в данный момент, вследствие чего оборудование генерирующих предприятий (ТЭС, АЭС, ГЭС и др.) должно работать с переменной нагрузкой. Отсюда следует, что математические модели, используемые в энергетике, должны содержать дополнительную переменную – нагрузку, что усложняет разработку МО систем управления энергетическими объектами. Наиболее востребованными являются математические модели, представляющие функции двух переменных, одной из которых является нагрузка.
Наиболее важные характеристики, необходимые для оптимального управления, определяются или корректируются на этапе наладки путем выполнения экспериментальных работ (испытаний), так как чисто теоретически (расчетным путем) невозможно учесть всю конкретику технологического процесса и оборудования.
Ниже представлена универсальная методика построения аппроксимирующей функции двух переменных, когда исходные данные представлены в виде таблицы, полученной в результате эксперимента или расчетным путем.
Основные понятия
Геометрическая интерпретация функции одной переменной Y(x) – линия на плоскости, 2D график, показывающий функциональную связь двух переменных.
Геометрическая интерпретация функции двух переменных Z(x, y) – поверхность в трехмерном пространстве x, y, Z, 3D график, наглядно показывающий функциональную связь трех переменных.
Функция трех переменных не имеет точной геометрической интерпретации в трехмерном пространстве; приближенно (дискретно) ее можно представить как набор поверхностей, вложенных одна в другую.
При объявлении (описании) функция должна иметь вид:
Имя функции (имена аргументов) = тело функции.
Пример: Z(x, y) = 5x3 + 1,12y2 – xy - 2x +18,
т.е. функция должна содержать пять частей (атрибутов): имя функции (Z), скобки и имена аргументов внутри них (x, y), знак равенства (=) и тело функции (5x3 + 1,12y2 – xy - 2x +18). Тело функции показывает, что функция делает со своими аргументами, когда им присваиваются конкретные значения.
Зависимость между величинами может быть представлена тремя способами: в виде таблицы, в виде графика, в виде формулы (аналитическое или символьное представление).
В данной статье под аппроксимацией понимается процедура перевода зависимости между величинами, изначально представленной в виде таблицы, в ту же зависимость, но представленную в аналитической форме, т.е. в виде формулы.
При разработке математического обеспечения АСУ полученные экспериментальным или расчетным путем табличные и графические зависимости должны быть переведены в аналитическую (символьную) форму, удобную для хранения и использования в микропроцессорах аппаратной части АСУ ТП с использованием процедуры аппроксимации.
Методику аппроксимации функцией двух переменных (аргументов) рассмотрим на примере построения эколого-экономической характеристики (ЭЭХ) установки селективного некаталитического восстановления (СНКВ) оксидов азота карбамидом, установленной на котле номинальной паропроизводительностью 1050 т/ч. СНКВ используется в качестве второй ступени снижения концентрации оксидов азота до нормативного значения в пылеугольных котлах, оснащенных топками с жидким шлакоудалением, в которых концентрация оксидов азота в дымовых газах особенно высока.
В качестве исходных используются следующие массивы данных, полученные экспериментальным и расчетным путем (рис.1.1, 1.2):
D – расход пара, т/ч, (нагрузка котла);
K – расход (подача) карбамида, г/с, (атмосфероохранное воздействие);
ΔC – снижение концентрации оксидов азота в установке СНКВ в результате подачи карбамида, мг/м3;
Z – эксплуатационные затраты на СНКВ, руб/ч.
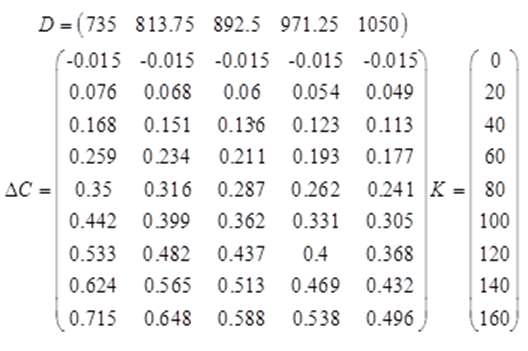
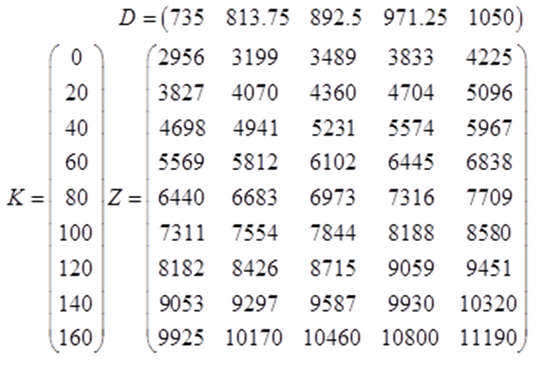
Процедуру (алгоритм) аппроксимации функцией Z(D, ΔC) Представим в виде последовательных шагов:
1. Строим график зависимостей Z(ΔC) для фиксированных значений D, т.е. отображаем поверхность набором линий на плоскости (см. рисунок 2):
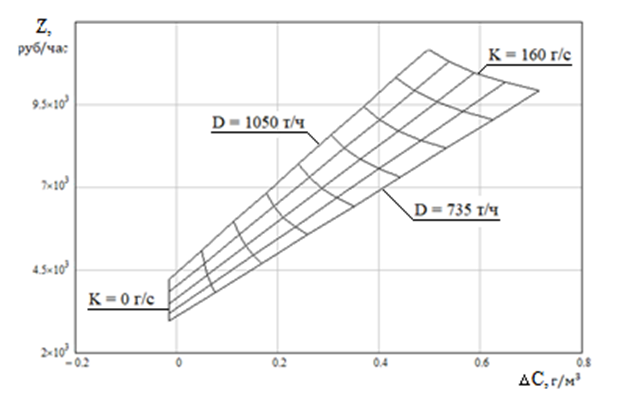
(Возможны два варианта решения поставленной задачи: при втором варианте строится график зависимостей Z от D для фиксированных значений ΔC. При этом методика остается прежней и конечный результат будет тем же самым. Пользователь сам выбирает тот вариант, который для него более удобен. Для варианта представления исходных данных так, как в рассматриваемом примере, более удобно отображать поверхность в виде семейства линий Z(ΔC) при фиксированных значениях D) .
.
2. Выбор структуры аппроксимирующей модели. Смотрим на график и решаем, каким выражением можно описать каждую линию Z(ΔC) при фиксированном D. Вид (структура) выражения должен быть одинаковым для всех линий семейства, только постоянные коэффициенты будут разные (их значения требуется определить). Рекомендуется начинать с простых структур типа полиномов (многочленов), увеличивая степень полинома или выбирая другой тип зависимости (гиперболический, логарифмический, экспоненциальный и т.п.), если полином не подходит. В рассматриваемом случае кривизна линий Z(ΔC) небольшая (линии близки к прямым), поэтому выбираем аппроксимирующую модель в виде полинома второй степени
a·ΔC2 + b·ΔC + c, (1)
где коэффициенты a, b и c зависят от D, но как, мы пока не знаем.
Если окажется, что кривизна линий Z(ΔC) существенно изменяется при изменении D, то выбирается аппроксимирующее выражение для моделирования кривой с максимальной кривизной; оно подойдет для кривых с меньшей степенью кривизны, только коэффициенты при высоких степенях ΔC будут малы или близки к нулю.
3. Проверка правильности выбора аппроксимирующей модели. Для этого нужно для каждой из линий Z(ΔC) найти значения коэффициентов a, b, c в выражении (1) и наложить полученные расчетные графики на исходные, при этом визуально будут видны отклонения. Допустимая приведенная к диапазону Z максимальная погрешность в расчетных точках не должна превышать требуемого значения, например, 2%. Допустимая погрешность аппроксимации зависит от погрешности исходных данных. Если, например, значения ΔC определялись экспериментально с использованием газоанализаторов с приведенной к диапазону погрешностью ±5% (класс точности приборов), то нет необходимости выполнять аппроксимацию с точностью ±0,5%, это не повысит итоговую погрешность полученной математической модели.
Для нахождения коэффициентов a, b, c для каждого значения D необходимо составить и решить систему из трех уравнений с тремя неизвестными. Например, для D0 = 735 т/ч система уравнений будет иметь вид:
Z0,0 = a·ΔC0,02 + b·ΔC0,0 + c Z4,0 = a·ΔC4,02 + b·ΔC4,0 + c
Z8,0 = a·ΔC8,02 + b·ΔC8,0 + c.
Численные значения Z0,0, ΔС0,0 … Z8,0, ΔС8,0 берутся из исходных таблиц. Решив систему с помощью любого доступного математического пакета (например, в Mathcad или в его отечественном эквиваленте SMath Studio), находим коэффициенты a0, b0, c0, соответствующие нагрузке D0. Подставив найденные значения a0, b0, с0 в (1), строим график функции (1), накладывая его на исходный при D = D0. Если максимальная (из всех расчетных точек) приведенная погрешность не превышает допустимой, аналогичным путем находим коэффициенты для остальных значений D. В итоге получаем три массива коэффициентов a = (a0, …, a4), b = (b0,…, b4), c = (c0,…, c4), в каждом 5 элементов, соответствующих пяти значениям D.
4. Строим графики зависимостей a(D), b(D), c(D).
5. По виду графиков подбираем аппроксимирующие выражения для функций a(D), b(D), c(D) аналогично пунктам 2, 3. От качества (точности) полученных аппроксимаций существенно зависит точность конечного результата.
6. Подставляем выражения (тела функций) a(D), b(D), c(D) в выражение (1). Получаем конечный результат, т.е. функцию двух переменных (2):
Z(D, ΔC) = a(D)·ΔC2 + b(D)·ΔC + c(D). (2)
Важно: полученная эмпирическая формула конечного результата (2) справедлива только для тех-же размерностей величин, что и в исходных данных.
7. Проверяем погрешности найденной эмпирической формулы для определения Z по формуле (2) в расчетных точках, т.е. для исходных значений D и ΔC, максимальная из них не должна превышать принятого допустимого значения. Следует избегать использования относительной погрешности, так как для значения функции Z, равного нулю, она будет «улетать» в бесконечность.
Заключение
Представленная методика позволяет получать аналитические 3D-модели с минимальным привлечением математических пакетов (использование их только для решения систем уравнений). Она дает возможность более гибко учитывать особенности, конкретику моделируемого объекта и может быть использована наладчиками технологического оборудования и систем управления, а также студентами, так как показывает и объясняет «кухню» математического моделирования, которая при использовании программного обеспечения скрыта от пользователя.
Понимание механизма, логики моделирования двухфакторных зависимостей дает возможность распространить рассмотренную методику на решение более сложной задачи моделирования трех, четырехфакторных зависимостей с получением аналитических моделей в виде функций трех, четырех аргументов. Объем вычислений (число решаемых уравнений, число определяемых постоянных коэффициентов) при этом существенно возрастает, но алгоритм решения несложен для понимания студентом или инженером.
Например, в процессе эксплуатации выяснилось, что характеристика оборудования F, ранее рассматриваемая как функция двух переменных с телом в виде выражения, содержащего x, y, a, b, c, где x, y – переменные, a, b, c, – постоянные коэффициенты, требует учета третьей переменной z с трансформацией F(x, y) в F1(x, y, z). Логически понятным способом такой трансформации является представление постоянных коэффициентов a, b, c функциями a(z), b(z), c(z) с последующим определением вида (структуры) этих функций с использованием методики аппроксимации функции двух переменных. При этом каждая линия на графике F(x) при фиксированном y превращается в семейство (пучок) линий каждая из которых соответствует дискретному значению z. При этом в теле F1 появляются новые постоянные d, e, f, g, . . ., число которых существенно больше, чем в исходной функции F, но это усложнение дает нам более адекватную и точную модель объекта.
В рассмотренном примере полученная математическая модель (2) (ЭЭХ установки СНКВ) загружается в память расчетной станции, предназначенной для оптимального управления выбросами оксидов азота тепловой электростанцией при работе с переменной нагрузкой. Она входит в состав целевой функции, позволяющей в режиме реального времени управлять выбросами отдельных энергетических котлов ТЭС, соблюдая экологические нормативы, но с минимумом затрат на атмосфероохранные мероприятия.
Автор: Парчевский В.М., НИУ "МЭИ", кафедра АСУ ТП
Автор: valpar






