Если вдруг автомобильный дилер скажет про свои автомобили, что у них под капотом двигатель, цикл которого состоит двух изотерм и двух адиабат и коэффициент полезного действия .., короче "Цикл Карно — идеальный термодинамический цикл". То Вы наверно покрутите у виска пальцем (к счастью не все покрутят и некоторые поймут и выслушают, может даже потом объяснят тем, кто хочет слушать) и пойдёте к другому. Но эти слова - правда и ничего кроме правды, но она вам не нужна.
Рубрика «аппроксимация»
Под капотом у ИИ
2025-08-09 в 10:42, admin, рубрики: аппроксимация, бизнес, интерполяция, искусственный интеллект, математика, теория вероятностей, центральная предельная теорема, численные методы, экстраполяцияBM YOLO: что, если вам не нужно умножать, чтобы распознавать?
2025-02-03 в 15:05, admin, рубрики: smart engines, yolo, аппроксимация, биполярный морфологический нейрон, детекция объектов, искусственный интеллект, машинное обучениеСовременные технологии глубокого обучения проникают в самые разные области нашей жизни — от автономных автомобилей до систем видеонаблюдения. Однако высокая вычислительная сложность традиционных нейронных сетей остается серьёзным препятствием на пути к их широкому применению на мобильных устройствах и встраиваемых системах.
Группа исследователей из Smart Engines представилаЧитать полностью »
Многофакторное аппроксимирование на платформе .Net. Часть первая. Теория
2025-02-02 в 6:16, admin, рубрики: C#, аппроксимация, регрессияВ современном мире анализа данных регрессионный анализ занимает центральное место, предоставляя мощные инструменты для выявления и количественной оценки взаимосвязей между переменными. Он позволяет исследователям и аналитикам не только описывать существующие зависимости, но и прогнозировать поведение систем на основе имеющихся данных. Одним из наиболее распространенных методов регрессионного анализа является метод наименьших квадратов, который стремится минимизировать сумму квадратов отклонений между наблюдаемыми и предсказанными значениями.
Уточнение процентилей с помощью полиномиальной аппроксимации
2024-09-05 в 14:05, admin, рубрики: аппроксимация, вероятности, квантили, квартили, плотность распределдения, полиномы, процентили, степень полиномаКогда заказчик просит определить процентили для дискретных значений и хочет получить точные значения в виде непрерывных величинЧитать полностью »
Как калькуляторы вычисляют синус?
2024-03-09 в 8:45, admin, рубрики: аппроксимация, косинус, ряды Тейлора, синус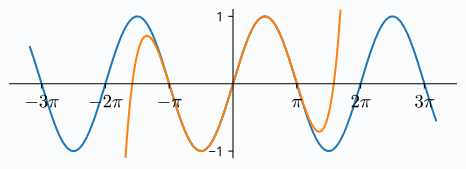
Введение
Синус, одна из фундаментальных тригонометрических функций, играет важнейшую роль в различных областях, включая математику, физику, проектирование и computer science. Процесс его вычисления нетривиален, особенно при реализации в электронных калькуляторах, где крайне важна эффективность и точность.
В предыдущих постах серии мы изучили, как Читать полностью »
Аппроксимация синуса: полиномы Чебышёва vs. ряды Маклорена
2021-10-09 в 12:35, admin, рубрики: C, Алгоритмы, аппроксимация, математикаВ комментариях к моей статье про быстрое вычисление синуса был задан вопрос: "А чем не устроило разложение в ряд Тейлора?"
Краткий ответ таков: хоть приближение при помощи рядов Тейлора (точнее - рядами Маклорена) и даёт меньшую ошибку при том же количестве вычислений, но оно не позволяет разбить аргумент на произвольное количество интервалов и тем самым увеличить точность вычислений.
Теперь более подробно.
При приближении синуса (и не только) полиномами Чебышёва используют следующее выражение:
Адаптивное разбиение кривых Безье 2-го и 3-го порядка
2020-06-14 в 19:39, admin, рубрики: python, аппроксимация, векторная графика, кривые безье, Программирование, Работа с векторной графикой
Уже год как я сменил работу на новую. В этой статье я хочу поделиться опытом, накопленным на прошлом месте. Здесь рассмотрены методы аппроксимации кривых Безье, а также обработка исключительных случаев, при которых простые алгоритмы показывают себя не очень хорошо. Все, кому близка тема векторной графики — прошу под кат.
Новое доказательство решает вопрос аппроксимации таких чисел, как пи
2019-09-17 в 7:00, admin, рубрики: аппроксимация, гипотеза Даффина-Шаффера, математика, Научно-популярноеДревние греки интересовались, можно ли приблизительно выразить иррациональные числа дробями. Доказав давнюю гипотезу Даффина-Шаффера, два математика дали исчерпывающий ответ.
Двоичная запись π бесконечна. Но бесконечное число дробей могут приближаться к этому числу со всё возрастающей точностью.
Глубокие провалы на числовой прямой не так неприступны, как могло показаться. Это одно из последствий нового значимого доказательства того, как сложные числа поддаются простым приближениям.
Доказательство разрешает задачу почти 80-летней давности, известную, как гипотеза Даффина-Шаффера. Тем самым оно даёт окончательный ответ, занимавший математиков с древних времён: при каких условиях возможно представлять иррациональные числа, длящиеся бесконечно долго – типа числа пи – простыми дробями типа 22/7? Доказательство устанавливает, что ответ на этот довольно общий вопрос обнаруживается в результате единственного вычисления.
Читать полностью »
Равномерное распределение точек на сфере
2019-07-22 в 5:56, admin, рубрики: Алгоритмы, аппроксимация, додекаэдр, золотое сечение, икосаэдр, математика, Работа с 3D-графикой, распределение точек, сфера, фибоначчиКак можно более равномерное распределение точек на сфере — невероятно важная задача в математике, науке и компьютерных системах, а наложение сетки Фибоначчи на поверхность сферы при помощи равновеликой проекции — чрезвычайно быстрый и эффективный метод аппроксимации для её решения. Я покажу, как благодаря незначительным изменениям его можно сделать ещё лучше.

Какое-то время назад этот пост появился на главной странице Hacker News. Его обсуждение можно прочитать здесь.
Введение
Задача равномерного распределения точек на сфере имеет очень долгую историю. Это одна из самых хорошо исследованных задач в математической литературе по сферической геометрии. Она имеет критическую важность во многих областях математики, физики, химии, в том числе в вычислительных методах, теории приближений, теории кодирования, кристаллографии, электростатике, компьютерной графике, морфологии вирусов и многих других.
К сожалению, за исключением нескольких особых случаев (а именно платоновых тел) невозможно идеально ровно распределить точки на сфере. Кроме того, решение задачи сильно зависит от критерия, который используется для оценки однородности. На практике используется множество критериев, в том числе:
- Упаковка и покрытие
- Выпуклые оболочки, ячейки Вороного и треугольники Делоне
- Ядра
-энергии Риса
- Кубатура и определители
Очень важно уяснить этот аспект: обычно не существует единственного оптимального решения этой задачи, потому что оптимальное решение, основанное на одном критерии, часто не является оптимальным распределением точек для других. Например, мы также выясним, что оптимизация упаковки необязательно создаёт оптимальную выпуклую оболочку и наоборот.
Ради краткости в этом посте мы рассмотрим только два критерия: минимальное расстояние упаковки и выпуклую оболочку/сетку Делоне (объём и площадь).
Читать полностью »
Трехмерный движок внутри запроса SQL
2019-01-11 в 8:21, admin, рубрики: 3d, 3d-движок, phong, postgresql, ray marching, raymarching, sql, sqlite, аппроксимация, аппроксимация квадратного корня, вавилонский метод, затенение по фонгу, квадратный корень, любителей читать теги, магическая константа, метод герона, ненормальное программирование, погрешность, поздравляю с первой пятницей, рекурсивные запросы, трассировка лучей, трехмерный движокНесколько лет назад на форуме SQL.ru решили провести сравнение реализаций трассировщиков лучей на разных языках программирования. К сожалению, моя заявка не может участвовать т.к. она не выводит надпись «PIXAR», поэтому публикую ее здесь.
Для чистоты эксперимента я использовал SQLite без расширений. Оказалось, что там нет даже функции SQRT.
WITH RECURSIVE numbers AS (SELECT 0 AS n UNION ALL SELECT n+1 FROM numbers WHERE n<89),
pixels AS (SELECT rows.n as row, cols.n as col FROM numbers as rows CROSS JOIN numbers as cols WHERE rows.n > 4 AND rows.n < 38 AND cols.n > 9 AND cols.n < 89),
rawRays AS (SELECT row, col, -0.9049 + col * 0.0065 + row * 0.0057 as x, -0.1487 + row * -0.0171 as y, 0.6713 + col * 0.0045 + row * -0.0081 as z FROM pixels),
norms AS (SELECT row, col, x, y, z, (1 + x * x + y * y + z * z) / 2 as n FROM rawRays),
rays AS (SELECT row, col, x / n AS x, y / n AS y, z / n AS z FROM norms),
iters AS (SELECT row, col, 0 as it, 0 as v FROM rays UNION ALL SELECT rays.row, rays.col, it + 1 AS it, v + MAX(ABS(0.7+v*x) - 0.3, ABS(0.7+v*y) - 0.3, ABS(-1.1+v*z) - 0.3, -((0.7+v*x) * (0.7+v*x) + (0.7+v*y) * (0.7+v*y) + (-1.1+v*z) * (-1.1+v*z)) * 1.78 + 0.28) AS v FROM iters JOIN rays ON rays.row = iters.row AND rays.col = iters.col WHERE it < 15),
lastIters AS (SELECT it0.row, it0.col, it0.v AS v0, it1.v AS v1, it2.v AS v2 FROM iters as it0 JOIN iters AS it1 ON it0.col = it1.col AND it0.row = it1.row JOIN iters AS it2 ON it0.col = it2.col AND it0.row = it2.row WHERE it0.it = 15 AND it1.it = 14 AND it2.it = 13),
res AS (SELECT col, (v0 - v1) / (v1 - v2) as v FROM lastIters)
SELECT group_concat(substr('$@B%8&WM#*oahkbdpqwmZO0QLCJUYXzcvunxrjft/|()1{}[]?-_+~<>i!lI;:,"^. ', round(1 + max(0, min(66, v * 67))), 1) || CASE WHEN col=88 THEN X'0A' ELSE '' END, '') FROM res;
:++++I
_________________________"
------/jucYJLQ0OZmwwwwwwwmmZO0QCUXcnj----------
???????:<}/nzJQOwqdbkhao***####**o LUcx|[<;????????????????
]]]]]]]]][[[ !{xu; o#MW&8%BB@@@@@ -ct[l ]]]]]]]]]]]??-
U[[[[[[[}}}}}}}}} ;1X] $$$$$$$$$$ cx[" [[[[[[[[]]]??
UUJJJCCCLLL{{{{{{{{{{ :|QZzffB$$$$$$ |Qu? {{{{{{}}}[[]]??-
YUUJJJCCCLLLQQ000OOO111111111 ,l!!; 111111111111{{}}[[]]??-
YUUJJJCCCLLLQQQ00OOOZZZmmmwww(((((((((((((((((((()))))))))))))11{{ i]??-
YYUUUJJCCCLLL ?fuv| ZZZmmmwwwqqqpppd||||||||||||||||||((())11{ i++i;??--
YYYUUUJJJ i Cmmwwwqqqppppdddbbbbk///////||(())11 }czfYuf{_--
XYYUUU Wwwwqqqpppddddbbbbkkkk/||(())) |j :zr)--
XXYYY; $$wqqqqpppddddbbbbk/|||(()) ^X Jcf-
XXXY $$$$xwqqqppppddddbbb/||(()) v LX-_
zXX! $$$$$$$nqqqqppppdddbb||(()) q mQX-
zzX> $$$$$$$$$$$$qqqqppppddd|(()) k dmL-_
zzl $$$$$$$$$$$$$$wqqqqppppd((() o W*kqOJ__
czz? $$$$$$$$$$$$$$$$$ wqqqqpp|(() O $$BadmQ__
ccc!1x $$$$$$$$ wwqqqq(() {$$$$$$$Babw0___
vcc<)xXQm W%@$$$$$$ mwwwwq()) %$$$$$@%W#adwQ___
vvcc>1rzCZqkoM&B$$ bmmwww)) )o$$$$B&MokpZL-__+
uvvvcc]tuUQmpkoM Zmmmm)1 J- &MohdmQU-__++
uuvvvcc{jvUQmp ZZZm)11 J: kpmQUc-__;
nuuuvvvcc}fuYL nOOZZ11 /| .0CXu}-_
nuuvvvccc-)jv !00OOO11{ ;/zvzvxt1--
vvvcccz+{ }QQ000O1{{ !~+~>?-
ccczz:<] : LQQQQ00{{}}[ ]??
zzzzXX ";I;" JCCCLLLLQQQ{}}[[]]]?
zzXXXYYYUUUUJJJCCCCLLL{}}[[]]]
XXYYYYUUUJJJJCCCC}}[[]]
YYYUUUUJJJJC}[[]
YUUUUJJ[[
UU
Под катом построчный разбор запроса. Как обычно, достаточно знания основ SQL и школьной математики.
Читать полностью »
