В комментариях к моей статье про быстрое вычисление синуса был задан вопрос: "А чем не устроило разложение в ряд Тейлора?"
Краткий ответ таков: хоть приближение при помощи рядов Тейлора (точнее - рядами Маклорена) и даёт меньшую ошибку при том же количестве вычислений, но оно не позволяет разбить аргумент на произвольное количество интервалов и тем самым увеличить точность вычислений.
Теперь более подробно.
При приближении синуса (и не только) полиномами Чебышёва используют следующее выражение:
При этом коэффициенты А0, А1 и т.д. рассчитываются заранее для какого-то участка функции.
При помощи рядов Маклорена синус вычисляется по следующей формуле:
Для удобства вычислений можно вынести повторяющиеся фрагменты за скобки. Например, так:
или так:
Для примера найдём значения синуса на интервале от 0 до 

График многочлена Чебышёва представляет собой фрагмент параболы, и пересекает график синуса в трёх точках, являющимися корнями многочлена.
График ряда Маклорена, начиная с левого края, почти совпадает с графиком синуса, и расхождение с ним начинается заметно на глаз только в правой трети диаграммы.
Графики ошибок аппроксимации выглядят так:
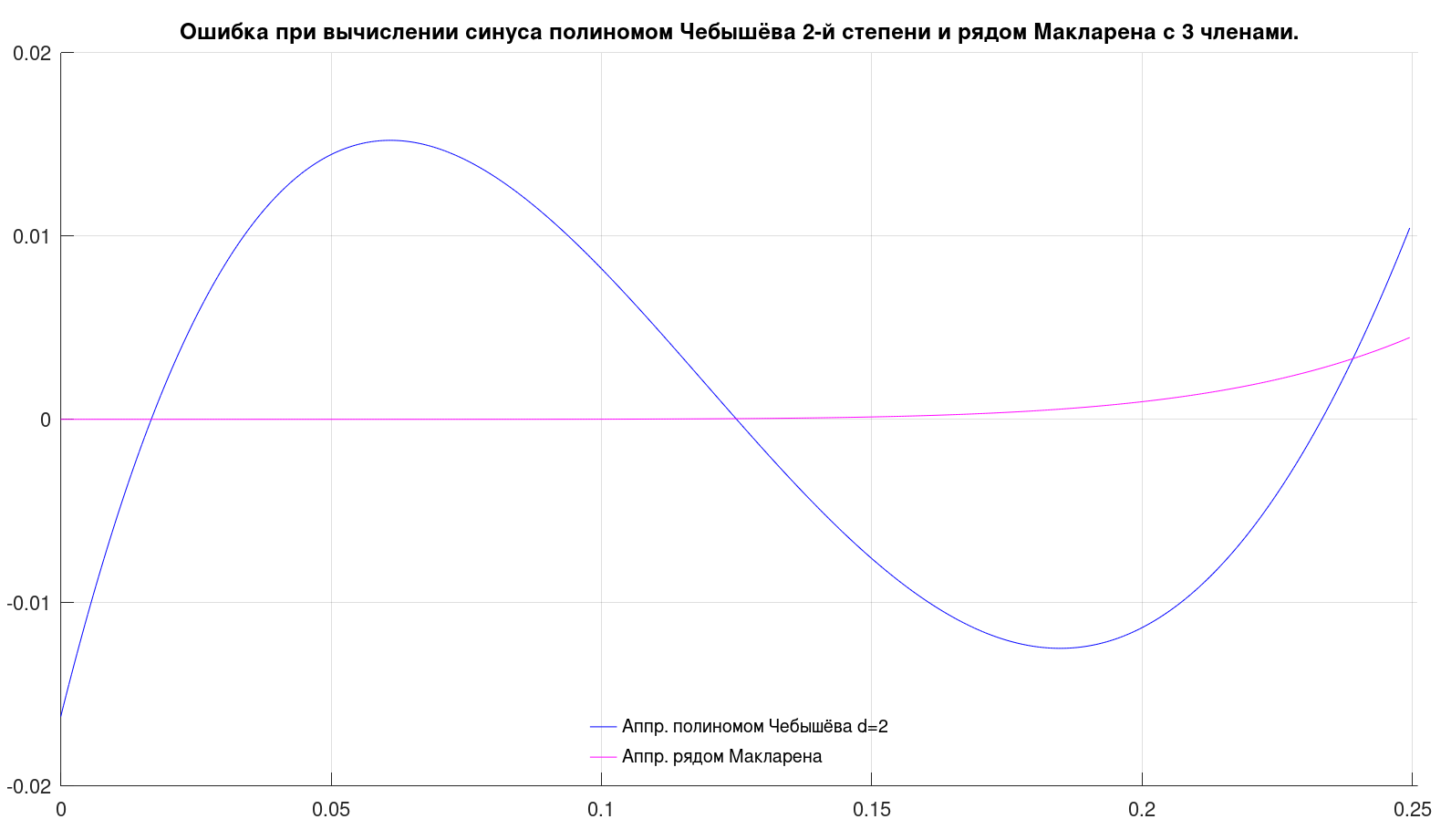
На них видно, что ошибка приближения полиномом Чебышёва в разы больше таковой у ряда Маклорена.
Теперь давайте посмотрим, как ошибки аппроксимации зависят от количества членов аппроксимирующей функции.
Графики ошибок аппроксимации рядами Маклорена разной длины выглядят так:

Графики ошибок аппроксимации полиномами Чебышёва имеют следующий вид:

Графики ошибок выглядят по разному, но в обоих случаях величина ошибки падает с увеличением количества членов ряда. При этом точность полинома Чебышёва уже на порядки хуже таковой у рядов Маклорена.
На следующей диаграмме показана сравнительная точность аппроксимации обоими методами в зависимости от количества членов ряда (полинома). Точность выражена в "дробных битах", численно равных минус логарифму ошибки по основанию 2:

Вычисления производились с использованием 80-битных числе с плавающей запятой (тип long double). Результаты аппроксимации сравнивались со значением синуса, полученными стандартной функцией sinl() из библиотеки С компилятора gcc.
Приближение при помощи рядов Маклорена (зелёная линия) даёт большую точность по сравнению с полиномами Чебышёва (синяя линия). Точность не растёт выше какого-то предела, это связано с ошибками округления при вычислениях.
Однако для аппроксимации полиномами Чебышёва полный период (от 0 до 
Вместо вывода. Пока что не существует идеального способа вычисления синуса, иначе не было такого их разнообразия. Подходящий способ выбирается как компромисс, исходя из заданных условий.
Автор: Виктор

