Недавно viktorpanasiuk опубликовал задачу о конфетах, которая «зацепила» многих, в том числе и меня. Задача практическая, от инженера-кондитера, формулировалась так: «Найти максимально допустимое отклонение массы конфеты при ее производстве, чтобы нетто коробки, состоящей из n=12 штук их, не выходило за пределы M=310±7 грамм в 90% случаев. Закон распределения считать нормальным».
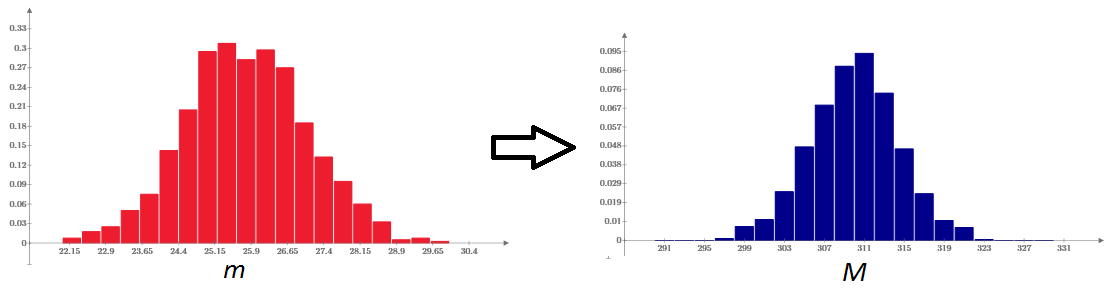
Автор решил задачу, исходя из предположения о нормальном распределении конфет по массе, и нашел среднюю массу конфеты (очевидно, равную µ=M/n=25.83 г) и стандартное отклонение σ=1.23 г. Использование метода Монте-Карло, т.е. генерация N*n случайных чисел с гауссовым распределением конфет со средним µ и стандартным отклонением σ, подтверждает правильность решения. Распределение масс коробок является гауссовым, и его параметры близки к найденным аналитически (расчеты в Mathcad Express в форматах MCDX и XPS прилагаются). На левом графике показана гистограмма плотности распределения (по массе) конфет, а на правом — соответственно, распределения коробок.
В финале процитированной статьи автор упоминает о немного измененной (на практике, более актуальной) задаче определения границ массы отдельной конфеты, при выходе за которые эту (чересчур большую или маленькую) конфету нужно отбросить, чтобы коробки удовлетворяли исходным условиям (310±7 г в 90% случаев). На мой взгляд, исходная статья уже содержит решение, надо лишь посмотреть на нее немного с другой точки зрения.
Читать полностью »