«Цель этого курса — подготовить вас к вашему техническому будущему.»
 Привет. Помните офигенную статью «Вы и ваша работа» (+219, 2372 в закладки, 375k прочтений)?
Привет. Помните офигенную статью «Вы и ваша работа» (+219, 2372 в закладки, 375k прочтений)?
Так вот у Хэмминга (да, да, самоконтролирующиеся и самокорректирующиеся коды Хэмминга) есть целая книга, написанная по мотивам его лекций. Мы ее переводи, ведь мужик дело говорит.
Это книга не просто про ИТ, это книга про стиль невероятно крутых людей. «Это не просто заряд положительного
Мы уже перевели 16 (из 30) глав.
Глава 14. Цифровые фильтры — 1
(За перевод спасибо Максиму Лавриненко, который откликнулся на мой призыв в «предыдущей главе».) Кто хочет помочь с переводом — пишите в личку или на почту magisterludi2016@yandex.ru
Теперь, когда мы изучили компьютеры и разобрались в том, как они представляют информацию, давайте обратимся к тому, как компьютеры обрабатывают информацию. Разумеется, мы сможем изучить лишь некоторые правила, поэтому сосредоточимся на основных принципах.
Большая часть того, что компьютеры обрабатывают, — это сигналы из разных источников, и мы уже обсуждали, почему они часто бывают в виде потока чисел из равноотстоящей системы выборки. Линейная обработка, единственная, на которую у меня хватает времени в рамках этой книги, подразумевает наличие цифровых фильтров. Чтобы продемонстрировать, как всё происходит в реальной жизни, сначала я расскажу вам о том, как я стал работать с ними, и далее о том, чем я занимался.
Во-первых, я никогда не ходил в офис моего вице-президента В. О. Бейкера; мы встречались только в коридорах, и обычно останавливались, чтобы поговорить всего несколько минут. Однажды, примерно в 1973-1974 годах, при встрече в зале, я сказал ему, что помню, как в то время, когда я пришёл в Bell Telephone Laboratories в 1946 году, компания постепенно переходила от релейного к электронному центральному управлению, и многие сотрудники тогда были переведены в другие подразделения, так как не смогли перейти на осциллографы и другие новейшие электронные технологии. Для него они представляли лишь серьёзные экономические потери, но для меня это была и социальная потеря, так как эти сотрудники были как минимум недовольны тем, что их перевели (хоть это и была их собственная ошибка). Далее я упомянул, что наблюдал аналогичную ситуацию, когда мы перешли со старых аналоговых компьютеров (по которым в Bell Telephone Laboratories было много экспертов, т. к. они разрабатывали большую часть технологий во время Второй мировой войны) на более современные цифровые компьютеры, — мы снова потеряли большое количество инженеров, и снова они были как экономической, так и социальной потерей.
Затем я заметил, что мы оба знаем, что компания в кратчайшее сроки собирается полностью перейти на цифровую передачу сигналов, в результате чего мы потеряем ещё большее количество недовольных инженеров. Таким образом, я пришел к выводу, что мы должны сейчас что-то сделать для улучшения ситуации, например, получить элементарные учебники и другие обучающие материалы, чтобы облегчить адаптацию сотрудников и потерять меньшее их количество. Он посмотрел мне прямо в глаза и сказал: «Да, Хэмминг, ты должен сделать это». И ушел! Более того, он продолжал ободрять меня через Джона Тьюки, с которым часто общался, поэтому я знал, что он следит за моими усилиями.
Что делать? Сначала я думал, что очень мало знаю о цифровых фильтрах, и, кроме того, меня это действительно не интересовало. Но разумно ли игнорировать своего вице-президента, а также убедительность собственных наблюдений? Нет! Возможные социальные потери были слишком большими для меня, чтобы не придавать им значения.
Поэтому я обратился к своему другу Джиму Кайзеру, одному из мировых экспертов в области цифровых фильтров того времени, с предложением приостановить его текущее исследование и написать книгу об электронных фильтрах, аргументируя это тем, что подведение итогов это естественный этап в развитии любого учёного. После некоторого давления он согласился написать книгу, и я подумал, что был спасён. Но периодические проверки его работы показывали, что он ничего не писал.
Чтобы спасти свой план я сделал ему следующее предложение: если он будет обучать меня за завтраками в ресторане (там будет больше времени на то, чтобы подумать, чем в столовой), чтобы помочь написать книгу совместно (хотя бы первую часть), то мы выпустим её под авторством Кайзера и Хэмминга. Он согласился!
Спустя некоторое время я перенял от него много знаний, и у меня была готова первая часть книги, но он сам всё ещё ничего не писал. Поэтому однажды я сказал: «Если ты так ничего и не напишешь, авторство книги в конечном итоге будет указано, как Хэмминга и Кайзера». И он согласился. В итоге, когда я закончил написание книги, а он ничего так и не написал, я сказал, что могу поблагодарить его в предисловии, но автором будет указан только Хэмминг, он согласился – и, несмотря на это, мы и по сей день хорошие друзья! Так появилась книга о цифровых фильтрах, которую я написал, и которая в конечном итоге прошла через три издания, всегда с хорошими советами от Кайзера.
Также благодаря книге я посетил много интересных мест, так как много лет проводил короткие, недельные курсы. Короткие курсы я начал давать ещё в процессе написания книги, так как мне нужна была обратная связь, и я предложил Отделу расширения Университета Калифорнии в Лос-Анджелесе (УКЛА) дать мне проводить курсы обучения, и они согласились. Это привело к годам преподавания в УКЛА, по одному разу в Париже, Англии — Лондоне и Кембридже, а также во многих других местах в США и, как минимум, дважды в Канаде. Выполнение того, что нужно было сделать, хотя я и не хотел этого делать, в конечном итоге окупилось.
Теперь перейдём к более важной части — о том, как я начал изучать новый предмет — цифровые фильтры. Изучение нового предмета — это то, что вам придётся делать много раз в своей карьере, если вы хотите быть лидером и не оставаться позади новейших разработок. Вскоре мне стало ясно, что в теории цифровых фильтров преобладают Ряды Фурье, которые я как раз изучал в колледже. Кроме того у меня было много дополнительных знаний благодаря моей работе по обработке сигналов, выполненной для Джона Тьюки, который был профессором из Принстона, гением и одним или двумя днями в неделю сотрудником Bell Telephone Laboratories. На протяжении почти десяти лет большую часть времени я был его вычислительной машиной.
Будучи математиком, я знал, как и все вы, что любой полный набор функций будет выполняться так же хорошо, как любой другой набор произвольных функций. Почему же тогда так отличаются Ряды Фурье? Я спрашивал у разных инженеров-электротехников, но не смог получить удовлетворительных ответов. Один из инженеров сказал, что переменные токи были синусоидальными, поэтому они использовали синусоиды, на что я ответил, что это не имело для меня никакого смысла. Вот тебе и обычное образование типичного инженера-электрика после окончания школы!
Поэтому я должен был подумать о базовых принципах, как я уже делал это при использовании компьютера с обнаружением ошибок. Что же на самом деле происходит? Я полагаю, многие из вас знают, что то, что мы хотим — это временное инвариантное представление сигналов, поскольку обычно нет естественного происхождения времени. Поэтому в качестве инструмента представления вещей мы приходим к тригонометрическим функциям (собственным функциям перевода) в виде, как рядов Фурье, так и интегралов Фурье.
Во-вторых, линейные системы, которые мы хотим на этом этапе, имеют те же собственные функции — комплексные экспоненты, которые эквивалентны действительным тригонометрическим функциям. Следовательно, простое правило: если у вас есть либо система с инвариантом во времени, либо линейная система, то вы должны использовать сложные экспоненты.
При дальнейшем углублении в тему я нашёл и третью причину для использования их в области цифровых фильтров. Существует теорема, которую часто называют «теоремой выборки Найквиста» (считалось, что она была известна задолго до того и даже была опубликована Уиттекером в форме, которую едва ли можно понять, даже если вы знаете теорему Найквиста), в которой говорится, что если у вас есть диапазон ограниченного сигнала и дискретные отсчёты в равных интервалах, не превышающих половины периода самого высокочастотного колебания, то исходный сигнал может быть восстановлен из дискретных отсчётов. Следовательно, процесс дискретизации не теряет никакой информации, когда мы заменяем непрерывный сигнал отсчётами с равными интервалами, при условии, что дискретные отсчёты охватывают всю реальную полосу сигнала. Частоту дискретизации часто называют «коэффициентом Найквиста» в честь Гарри Найквиста, за стабильность сервоприводов, а также другие вещи. Если вы проецируете функцию без полосы пропускания, то более высокие частоты «накладываются» на более низкие, так сказал Тьюки, чтобы описать тот факт, что высокая частота появится позже в качестве низкой частоты в диапазоне Найквиста.
То же самое неверно для любого другого набора функций, скажем степеней t. При одинаковых интервалах выборки и восстановления одна высокая степень t станет многочленом (много вариантов) более низких степеней t.
Таким образом, существуют три веские причины для функций Фурье: (1) инвариантность во времени, (2) линейность и (3) восстановление исходной функции из одинаковых интервалов выборок проста и понятна.
Поэтому мы будем анализировать сигналы в терминах функций Фурье, и мне не нужно обсуждать с инженерами-электротехниками, почему мы обычно используем сложные показатели как частоты вместо реальных тригонометрических функций. У нас есть линейная операция, и когда мы помещаем сигнал (поток чисел) в фильтр, выводится другой поток чисел. Естественно, если не из курса линейной алгебры, то из других предметов, таких как курс дифференциальных уравнений, возникает вопрос, какие функции входят и выходят без изменений, кроме шкалы? Как отмечалось выше, они являются сложными экспонентами; это собственные функции линейных, инвариантных по времени, выборочных систем с одинаковыми интервалами.
И вот ведь как, знаменитая передаточная функция — это собственные значения соответствующих собственных функций! Когда я спрашивал различных инженеров-электриков о том, что такое передаточная функция мне никто не сказал об этом! Да, когда им указывали, что это то же самое, им приходилось согласиться, но сами они об этом, кажется, никогда не задумывались! В их сознании была одна и та же идея, но в двух и более различных образах, и они и не подозревали о какой-либо связи между ними! Всегда начинайте с базовых принципов!
Теперь давайте обсудим «Что такое сигнал?». В природе есть много сигналов, которые являются непрерывными, и которые мы поэтому делим на дискретные отсчёты и далее оцифровываем (квантуем). Обычно сигналы являются функцией времени, но любой эксперимент в лаборатории, который использует напряжения с одинаковыми интервалами, например, и фиксирует соответствующие отклики, также является цифровым сигналом. Таким образом, цифровой сигнал является равномерно распределенными измерениями последовательности в виде чисел, и мы получаем из цифрового фильтра еще один равномерно распределенный набор чисел. Допускается обработка и неравномерно разнесенных данных, но я не буду рассматривать их здесь.
Квантование сигнала на один из нескольких уровней выхода часто имеет удивительно малый эффект. Вы все видели изображения, квантованные на два, четыре, восемь и более уровней, и даже изображение двух уровней обычно можно распознать. Я не буду рассматривать квантование здесь, поскольку это обычно небольшой эффект, хотя временами это очень важно.
Следствием выборки с одинаковыми интервалами является наложение, частота выше частоты Найквиста (которая имеет два отсчёта в цикле) будет наложена на более низкую частоту. Это простое следствие тригонометрического тождества
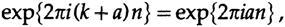
где a — положительный остаток после удаления целого числа вращений, k (мы всегда используем вращения при обсуждении результатов и используем радианы при применении исчисления, так же, как мы используем десятичные и базовые натуральные логарифмы), и n — количество шагов. Если а > 1/2, то мы можем написать
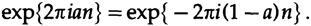
Таким образом, наложенный диапазон будет меньше 1/2 оборота, плюс-минус. Если мы используем две реальные тригонометрические функции, sin и cos, то мы получаем пару собственных функций для каждой частоты, и диапазон вращения будет от 0 до 1/2 оборотов, а при использовании комплексной экспоненциальной записи мы получим одну собственную функцию для каждой частоты, но теперь диапазон будет достигать от -1/2 до 1/2 оборотов.Такое предотвращение множественных собственных значений является одной из причин, почему сложные частоты намного легче обрабатываются, чем реальные синусоидальные и косинусные функции. Максимальная частота дискретизации, для которой наложение не происходит, — это два отсчёта в цикле, такая частота называется частотой Найквиста. Из отсчётов исходный сигнал не может быть определен с точностью до наложенных частот, только основные частоты, которые попадают в основной интервал неустановленных частот (-1/2 до 1/2), могут быть определены однозначно. Сигналы от различных наложенных частот переходят на одну частоту диапазона и алгебраически складываются; это то, что мы получаем в результате выполнения дискретизации. Отсюда добавление или сокращение может произойти во время наложения, и мы не можем знать какой изначальный наложенный сигнал у нас был. Из максимальной частоты дискретизации невозможно выразить результат от 1, следовательно, не наложенные частоты должны быть в пределах диапазона.
Мы будем растягивать (сжимать) время, чтобы мы могли измерять частоту дискретизации 1 раз в единицу времени, потому что это значительно упрощает и позволяет распространить данные от милли и микросекунд до таких интервалов, которые могут занять несколько дней или даже лет между отсчётами. Всегда разумно перенимать стандартную систему счисления и структуру
Наложение — это фундаментальный эффект дискретизации, оно не имеет ничего общего с обработкой сигналов. Мне было удобно думать, что как только снимаются отсчёты, все частоты находятся в диапазоне Найквиста, и, следовательно, нам не нужно рисовать периодические продолжения чего-либо, так как другие частоты больше не существуют в сигнале — после дискретизации высокие частоты переходят в нижний диапазон и перестают существовать. Как же я ошибался! Акт дискретизации производит наложенный сигнал, который мы должны использовать.
Теперь я перехожу к трем историям, в которых используются только идеи дискретизации и наложения. В первой истории я пытался вычислить численное решение системы из 28 обыкновенных дифференциальных уравнений, и я должен был знать, какую скорость дискретизации мне нужно использовать (размер шага решения — это частота дискретизации, которую вы используете), поскольку, если бы она была вдвое меньше, чем ожидалось, то счётчик вычислений будет примерно в два раза больше. В наиболее популярных и практических методах численного решения математическая теория рассчитывает размер шага по пятой производной. Кто мог знать об этом? Никто. Но если рассматривать шаг в рамках дискретизации, наложение начинается с двух отсчётов для самой высокой частоты, при условии, что у вас есть данные от минуса до плюс бесконечности. Я интуитивно понимал, что при наличии только короткого диапазона из максимум пяти точек данных, мне потребуется примерно в два раза больше, или 4 отсчёта за цикл. И, наконец, при наличии данных только с одной стороны, возможен, еще один фактор удвоения; всего 8 отсчётов за цикл.
Затем я сделал две вещи: (1) разработал теорию и (2) провел численные тесты на простом дифференциальном уравнении
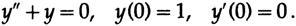
Оба они показали, что при 7 отсчётах за цикл, вы получаете приблизительную точность (за шаг), а при 10 — абсолютную. Так что я объяснил всё, как есть и запросил высшие частоты в ожидаемом решении. Справедливость моей просьбы была оценена, и через несколько дней мне сказали, что я должен беспокоиться о частотах до 10 циклов в секунду, а те, что выше не моя забота. И это было правильно, и ответы были удовлетворительными. Теорема дискретизации в действии!
Вторая история включает в себя замечание, сделанное мне случайно в залах Bell Telephone Laboratories о том, что у какого-то субподрядчика Западного побережья возникли проблемы с имитацией запуска ракеты Nike, он использовал от 1/1000 до 1/10 000 второго интервала. Я сразу же засмеялся и сказал, что это должно быть какая-то ошибка, так как для модели, которой они пользовались, было бы достаточно от 70 до 100 отсчётов. Оказалось, что у них было двоичное число, смещённое на 7 позиций влево, в 128 раз большее! Отладка большой программы на основе теоремы дискретизации!
Третья история о том, как группа в военно-морской аспирантуре модулировала очень высокочастотный сигнал до момента, где они могли бы сделать отсчёт, согласно теореме дискретизации, как они ее понимали. Но я понял, что если они с умом поделили высокую частоту, тогда акт дискретизация будет модулировать сам себя (накладываться на него). После нескольких дней споров они всё таки сняли стойку с низкочастотным оборудованием, и тогда остальная часть оборудования стала работать лучше! И в этот раз мне понадобилось только твёрдое понимание эффектов наложения при дискретизации. Это еще один пример того, почему вам нужно хорошо знать базовые принципы; остальное вы сможете легко додумать, и в результате знать то, о чём вам никогда никто не говорил.
Рисунок 14.I
Дискретизация — это фундаментальный подход, который мы используем при обработке данных в процессе работы за цифровыми компьютерами. Теперь, когда мы понимаем, что такое сигнал, и что дискретизация делает с сигналом, мы можем смело переходить к более подробному рассмотрению процессов обработки сигналов.
Сначала мы обсудим не рекурсивные фильтры, целью которых является передача некоторых частот и остановка других. Впервые проблема проявилась в телефонной компании, когда у них была теория, что если одно голосовое сообщение переместило (модулировало) все свои частоты на пределы другого диапазона, тогда два сигнала могут быть добавлены и отправлены по тем же проводам, и на другом конце они бы отфильтровывались и разделялись, а высший из них — уменьшался (демодулировался) назад до его исходных частот. Это смещение просто умножается на синусоидальную функцию и выбирает одну полосу (однополосная модуляция) из двух частот, которые возникают по следующему тригонометрическому тождеству (на этот раз мы используем вещественные функции)
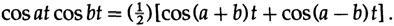
Нет ничего загадочного в изменении частоты (модуляции) сигнала, это не более чем вариант тригонометрического тождества.
Нерекурсивные фильтры, которые мы рассмотрим в начале, в основном относятся к типам сглаживания, где входными значениями являются значения u(t)=u(n)=un, а выходными — yn
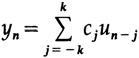
с Cj=C-j (коэффициенты симметричны относительно среднего значения C0).
Мне нужно напомнить вам о методе наименьших квадратов, поскольку это играет фундаментальную роль в том, что мы собираемся делать, для этого я разработаю сглаживающий фильтр, чтобы показать вам, как создаются фильтры. Предположим, что у нас есть сигнал с добавлением «шума» и его нужно сгладить, удалить шум. Мы предположим, что вам кажется разумным установить прямую линию в 5 последовательных точек данных в виде наименьших квадратов, а затем взять среднее значение на линии как «сглаженное значение функции» в этой точке.
Для математического удобства мы выбираем 5 точек при t = -2, -1,0,1,2 и устанавливаем
прямую линию,
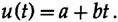
Метод наименьших квадратов говорит, что мы должны минимизировать сумму квадратов различий между данными и точками на линии, т. е. минимизировать
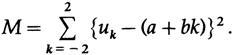
Какие параметры нужно использовать для дифференциации, чтобы найти минимум? Это a и b, а не t (теперь дискретная переменная k) и u. Линия зависит от параметров a и b, и это часто
камень преткновения для ученика; параметры уравнения являются переменными для минимизации! Следовательно, при дифференцировании по а и b и приравнивании производных к нулю для получения минимума имеем
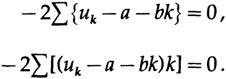
В этом случае нам нужно только a, значение линии в средней точке, следовательно, используем (некоторые из сумм для последующего использования),
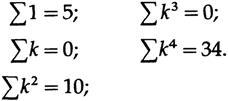
из верхнего уравнения имеем
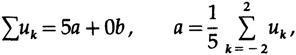
что является просто средним из пяти смежных значений. Когда вы задумаетесь о том, как выполнить вычисление для a, сглаженное значение, подумайте о данных в вертикальном столбце, рис. 14., с коэффициентами, равными 1/5, как текущее взвешивание данных; вы можете представить себе окно, через которое вы смотрите на данные, причем «форма» окна является коэффициентом фильтра, и этот случай сглаживания является однородным по размеру.
Если бы мы использовали точки, симметрично расположенные на расстоянии 2k+1, мы все равно получили бы среднее из точек данных как сглаженное значение, которое должно было устранить шум.
Предположим, что вместо прямой мы сгладили квадратичную фигуру, рис. 14. (III, 326;
2004: 232)
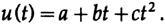
Установив разность квадратов и дифференцируя это время относительно a, b и c, получим:
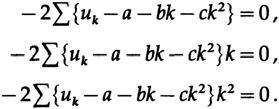
Опять же нам нужно только a. Переписывая первое и третье уравнения (среднее не включает a) и вставляя известные суммы сверху, мы имеем
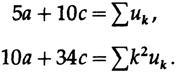
Чтобы исключить c, которая нам не нужна, умножим верхнее уравнение на 17 и нижнее уравнение на 5 и сложим, чтобы получить
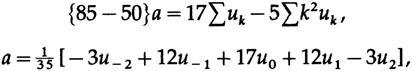
и на этот раз наше «окно сглаживания» не имеет однородных коэффициентов, но имеет некоторые с отрицательными значениями. Не стоит беспокоиться из-за этого, так как мы говорим об окне метафорически, и, следовательно, возможна отрицательная передача.
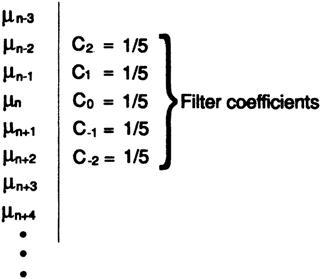
Рисунок 14.II
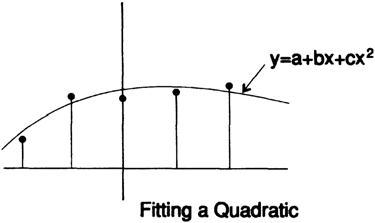
Рисунок 14.III
Если теперь мы переместим эти два наименьших квадрата на формулы сглаживания в их собственные места вокруг точки n, мы получим
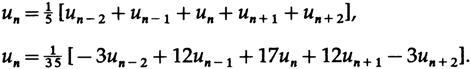
Теперь мы спросим, что будет на выходе, если на входе мы поместим чистую собственную функцию. Мы знаем, что так как уравнения линейны, они должны возвращать собственную функцию, но умноженную на собственное значение, соответствующее частоте собственной функции, значение передаточной функции на этой частоте. Взяв верхнюю часть двух формул, мы имеем
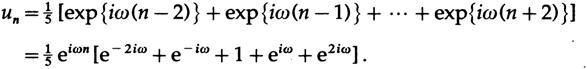
Следовательно, собственное значение на частоте ω (передаточная функция) по элементарной тригонометрии,
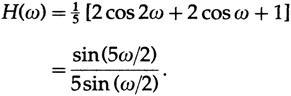
В параболическом сглаживающем случае мы получим
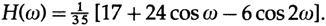
Они легко отобразятся вдоль со сглаживанием 2к+1 прямыми линиями, рис. 14.IV.
Формулы сглаживания имеют центральную симметрию по своим коэффициентам, а дифференцирующие формулы имеют нечетные симметрии. Из очевидной формулы
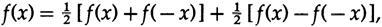
мы видим, что любая формула представляет собой сумму нечетной и четной функции, поэтому любой нерекурсивный цифровой фильтр представляет собой сумму сглаживающего фильтра и дифференцирующего фильтра. Когда мы справились с этими двумя особыми случаями, мы получаем общий случай.
Для сглаживания формул мы видим, что кривая собственных значений (передаточная функция) является разложением Фурье в косинусах, а для формулы дифференцирования — разложением в синусах. Таким образом, мы приводим, учитывая передаточную функцию, которую вы хотите достичь, к проблеме разложений Фурье данной функции.
Теперь кратко переформулируем ряды Фурье. Если предположить, что произвольная функция f (t) представлена
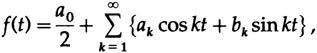
мы используем условия ортогональности (их можно найти с помощью элементарной тригонометрии и простых интегрирований):
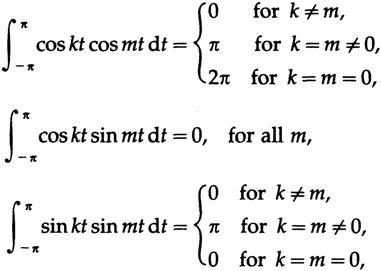
мы получаем
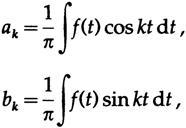
и так как мы использовали a0/2 для первого коэффициента, та же формула для ak справедлива и для случая k= 0. В комплексных обозначениях это, конечно, намного проще.
Далее нам нужно доказать, что соответствие любого ортогонального множества функций дает наименьшее квадратичное соответствие. Пусть множество ортогональных функций есть {fk(t)} с весовой функцией w (t)≥0. Ортогональность означает
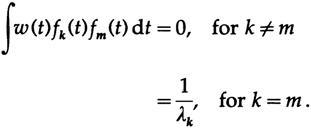
Как и выше, формальное расширение даст коэффициенты
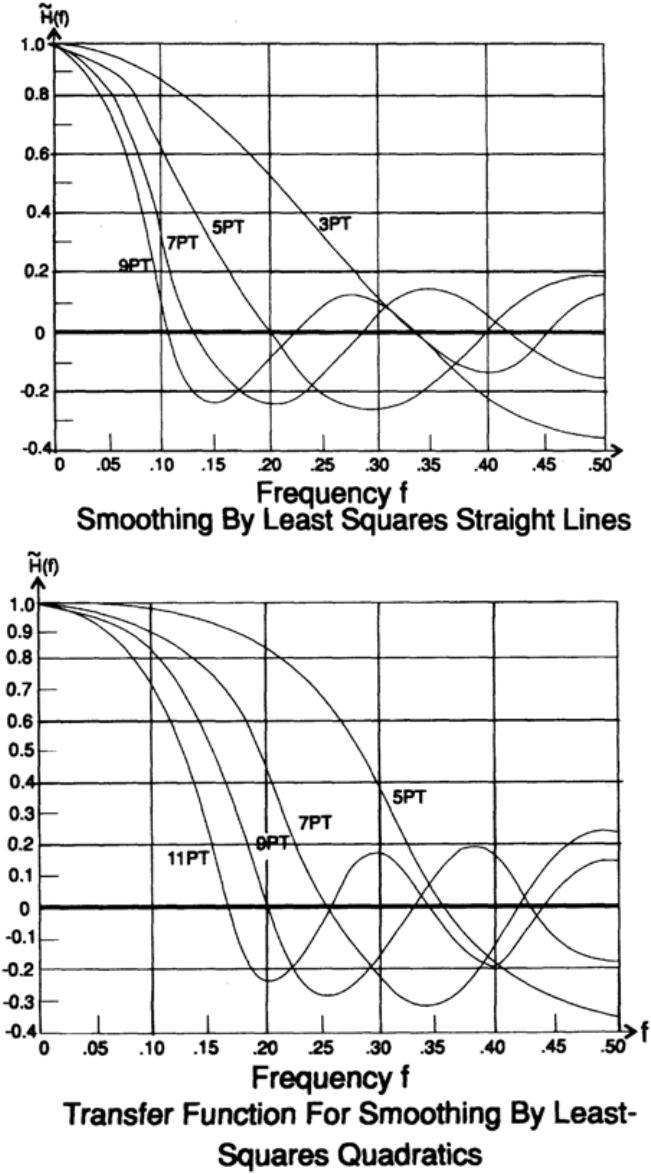
Рисунок 14.IV
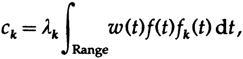
где
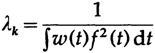
когда функции вещественны, и в случае комплексных функций мы умножаем на комплексно-сопряженную функцию.
Теперь рассмотрим аппроксимацию наименьших квадратов полного набора ортогональных функций с использованием коэффициентов (капиталов) Ck. У нас есть
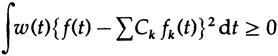
для минимизации. Дифференцируем по Cm и получаем
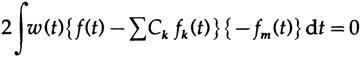
и из перестановки видно, что Ck=ck. Следовательно, всякая ортогональная функция подходит для наименьших квадратов, независимо от множества используемых ортогональных функций.
Если мы будем следить за неравенством, то мы получим в общем случае неравенство Бесселя
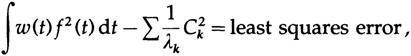
для числа коэффициентов, взятых в сумме, и это обеспечивает выполнение теста при достаточном количестве членов в конечном приближении. На практике это оказалось очень полезным руководством для определения количества членов в разложении Фурье.
Продолжение следует...
Кто хочет помочь с переводом — пишите в личку или на почту magisterludi2016@yandex.ru
Кстати, мы еще запустили перевод еще одной крутейшей книги — «The Dream Machine: История компьютерной революции»)
- Intro to The Art of Doing Science and Engineering: Learning to Learn (March 28, 1995) (в работе) Перевод: Глава 1
- «Foundations of the Digital (Discrete) Revolution» (March 30, 1995) Глава 2. Основы цифровой (дискретной) революции
- «History of Computers — Hardware» (March 31, 1995) Глава 3. История компьютеров — железо
- «History of Computers — Software» (April 4, 1995) Глава 4. История компьютеров — Софт
- «History of Computers — Applications» (April 6, 1995) Глава 5. История компьютеров — практическое применение
- «Artificial Intelligence — Part I» (April 7, 1995) (в работе)
- «Artificial Intelligence — Part II» (April 11, 1995) (в работе)
- «Artificial Intelligence III» (April 13, 1995) Глава 8. Искуственный интеллект-III
- «n-Dimensional Space» (April 14, 1995) Глава 9. N-мерное пространство
- «Coding Theory — The Representation of Information, Part I» (April 18, 1995) (в работе)
- «Coding Theory — The Representation of Information, Part II» (April 20, 1995)
- «Error-Correcting Codes» (April 21, 1995) (в работе)
- «Information Theory» (April 25, 1995) (в работе, Горгуров Алексей)
- «Digital Filters, Part I» (April 27, 1995) Глава 14. Цифровые фильтры — 1
- «Digital Filters, Part II» (April 28, 1995) в работе
- «Digital Filters, Part III» (May 2, 1995)
- «Digital Filters, Part IV» (May 4, 1995)
- «Simulation, Part I» (May 5, 1995) (в работе)
- «Simulation, Part II» (May 9, 1995) готово
- «Simulation, Part III» (May 11, 1995)
- «Fiber Optics» (May 12, 1995) в работе
- «Computer Aided Instruction» (May 16, 1995) (в работе)
- «Mathematics» (May 18, 1995) Глава 23. Математика
- «Quantum Mechanics» (May 19, 1995) Глава 24. Квантовая механика
- «Creativity» (May 23, 1995). Перевод: Глава 25. Креативность
- «Experts» (May 25, 1995) Глава 26. Эксперты
- «Unreliable Data» (May 26, 1995) (в работе)
- «Systems Engineering» (May 30, 1995) Глава 28. Системная Инженерия
- «You Get What You Measure» (June 1, 1995) Глава 29. Вы получаете то, что вы измеряете
- «How Do We Know What We Know» (June 2, 1995) в работе
- Hamming, «You and Your Research» (June 6, 1995). Перевод: Вы и ваша работа
Кто хочет помочь с переводом — пишите в личку или на почту magisterludi2016@yandex.ru
Автор: Алексей






