Подбираем пароль к индийскому ИНН за две секунды, или зачем брутфорсу математика

В Индии есть местный аналог нашего ИНН — «адхар». К нему прикручена электронная система «еАдхар». В «еАдхаре» каждое письмо блокируется паролем. И всё бы хорошо, но пароль составляется по простому шаблону: первые четыре буквы имени капсом плюс год рождения.

Четыре заглавные буквы и четыре цифры. Из них можно составить 2 821 109 907 456 комбинаций. Если проверять тысячу комбинаций в секунду, на один пароль уйдёт лет девяносто.

Долговато. Может ускоримся в пару (миллиардов) раз?

92 года → 52 дня. Группируем

С тремя триллионами комбинаций мы чуть-чуть хватили лишнего. Всё-таки шаблон известен:

([A-Z][A-Z][A-Z][A-Z])  ([0–9][0–9][0–9][0–9])
  (4 заглавные буквы)         (4 цифры)
      (Группа 1)              (Группа 2)

Если учесть этот шаблон, то строки вроде S2N65GE1 можно сразу отбросить. Сколько тогда получится комбинаций?

Первая группа — четыре буквенных символа. 26 вариантов, 4 позиции, получаем:

4 позиции по 10 цифр, аналогично:

Из этого получаем суммарное число комбинаций:

Прикинем, насколько быстрее теперь будет брутфорс. Снова исходим из 1000 попыток в секунду:

Или 52 дня, 21 час, 22 минуты и 40 секунд. Вместо 92 лет. Неплохо. Но всё равно долго. Что ещё можно сделать? То же самое — уменьшить количество комбинаций.

52 дня → 12 часов. Включаем здравый смысл

Первая и вторая группа — не случайный набор символов, а первые буквы имени и год рождения. Начнём с года рождения.

Подбирать пароли для родившихся в 1642 или 2594 смысла нет. Так что диапазон комбинаций можно смело уменьшить с 0000–9999 до 1918–2018. Так мы охватим плюс-минус всех ныне живущих в возрасте от 0 до 100 лет. Благодаря этому сокращается и число комбинаций, и время соответственно:

Или 12 часов, 41 минута и 37 секунд.

12 часов → 2 минуты. Жертвуем точностью

12 часов — это классно, но… We need to go deeper.

Сейчас у нас есть 45 миллионов комбинаций, которые точно покрывают всех пользователей «еАдхара». Но что если пожертвовать их малой долей ради прироста скорости?

Цифровые комбинации мы довели до совершенства. С буквами сделаем нечто подобное. Логика проста: нет года рождения 9999, и точно так же нет индийского имени c «AAAA» в начале. Но как определить все подходящие комбинации?

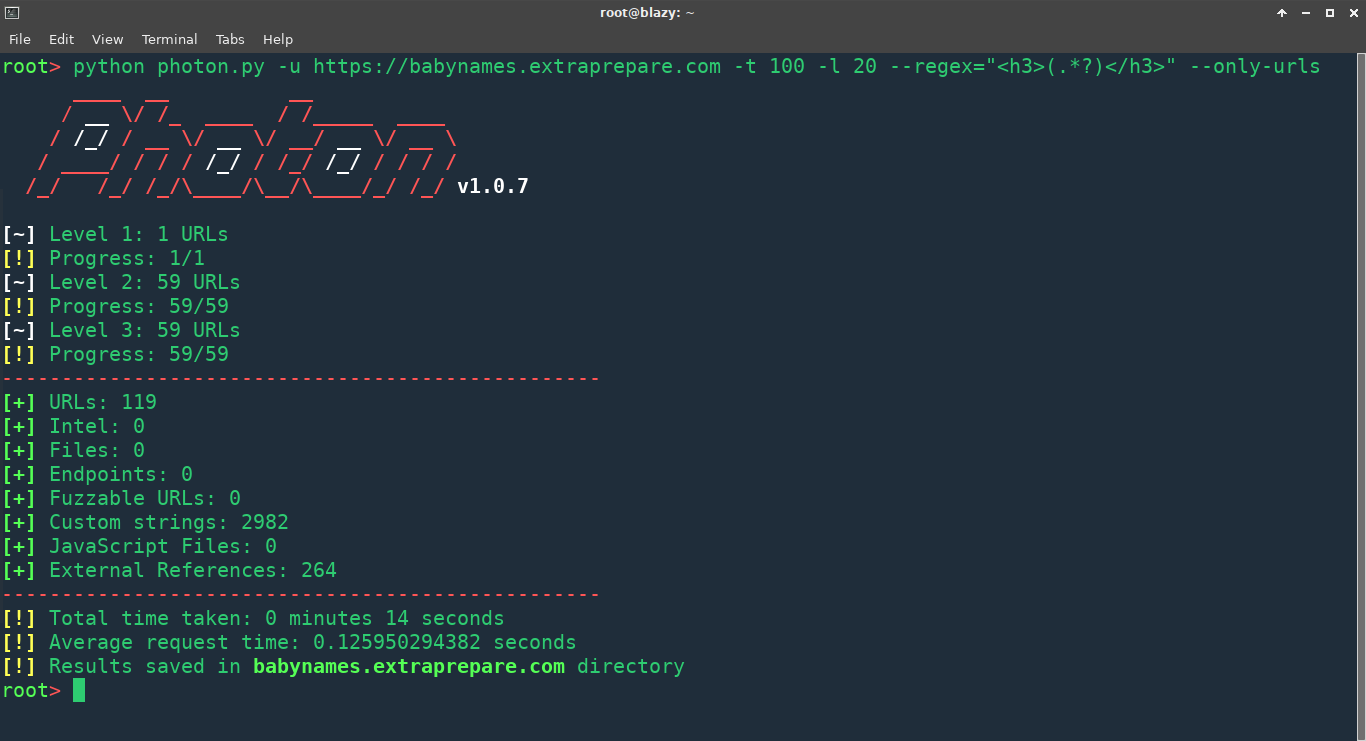
Я собрал индийские имена с сайта-каталога, в этом мне очень помог Photon. В итоге получилось 3 283 уникальных имени. Осталось обрезать первые четыре буквы и убрать дубликаты:

grep -oP ”^w{4}” custom.txt | sort | uniq | dd conv=ucase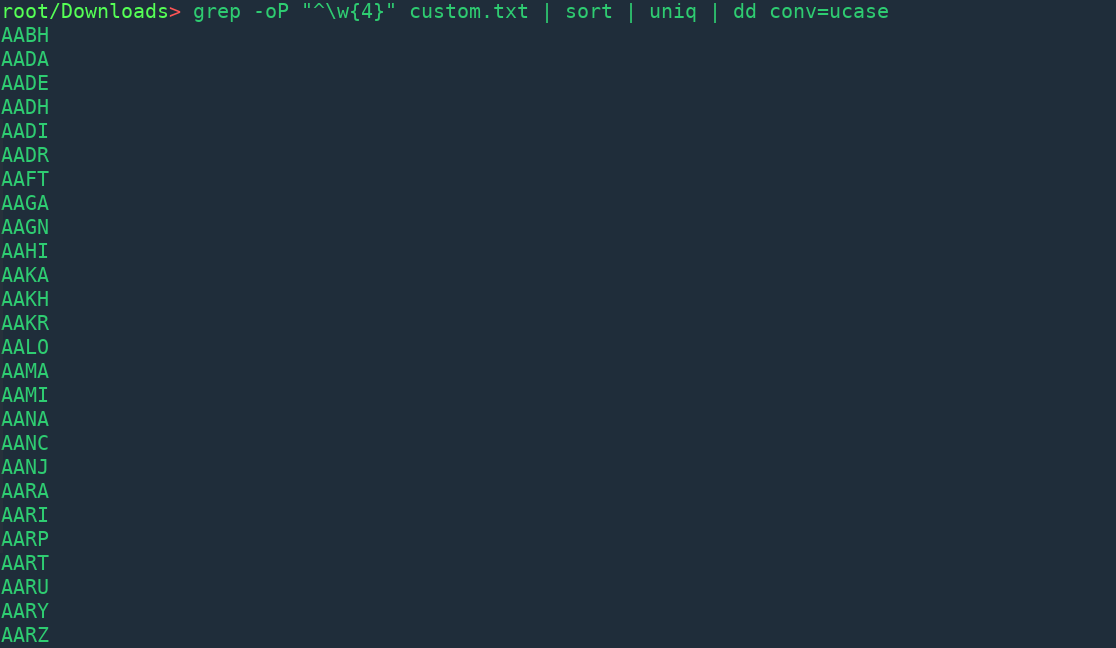

Получилось 1 598 префиксов! Дубликатов оказалось довольно много, потому что первые четыре буквы в таких именах как «Sanjeev» и «Sanjit» — одинаковые.

1 598 префиксов — маловато для полуторамиллиардного населения? Согласен. Но не забывайте, что это именно префиксы, а не имена. Я выложил получившийся список на Гист. На самом деле их должно быть больше. Можно заморочиться, собрать 10 000 имён с других сайтов и получить 3 000 уникальных префиксов, но у меня не было на это времени. Так что будем отталкиваться от 1 598.

Подсчитаем, сколько времени нужно теперь:

Или 2 минуты и 39.8 секунды.

2 минуты → 2 секунды. Википедия в помощь

2 минуты 40 секунд — это время, которое понадобится на перебор всех комбинаций. А что если одиннадцатая комбинация правильная? Или последняя? Или первая?

Сейчас перечень комбинаций отсортирован по алфавиту. Но это бессмысленно — кто сказал, что имена на «А» встречаются чаще, чем на «B», или что годовалых детей больше, чем семидесятилетних стариков?

Нужно учесть вероятность каждой комбинации. На Википедии пишут:

В Индии более 50% населения младше 25 лет и более 65% — младше 35.

Исходя из этого, вместо перечня 1–100 можно попробовать такой:

25-01 (в обратном порядке, потому что с возрастом выше шанс того, что у человека есть адхар)
25 - 35
36 – 100

Тогда получается, что вероятность первых комбинаций возрастает до 50%. Мы взломали половину паролей за секунд! В следующие секунд, мы подберём ещё 15% паролей. Итого — 65% паролей за 55.9 секунды.

Теперь к именам.

В Гугле легко найти ТОП-100 имён любой страны. Исходя из данных по Индии, я передвинул соответствующие комбинации наверх списка. Будем считать, что 15% населения Индии носит популярные имена. Значит 15% паролей можно взломать практически мгновенно.

Индусы — 80% населения Индии. Значит, если поставить индуистские имена выше в списке, то это ускорит 80% попыток. После предыдущего шага у нас осталось попыток. Если из них 80% имён — индуистские, то 79% (оставляем 1% на популярные, но не индуистские имена) мы взломаем в следующие 65% попыток.

Посчитаем всё вместе, с учётом возрастной статистики. Разобьем на группы:

100: Общее количество {
    50: от 00 до 25 лет {
        7: популярные имена,
        43: непопулярные имена {
            34: индусы,
            9: не индусы
        }
    }
    15: от 26 до 35 лет {
        3: популярные имена,
        13*: непопулярные имена {
            10: индусы,
            3: не индусы
        }
    }
    45: от 36 до 100 лет {
        7: популярные имена,
        38: непопулярные имена {
            30: индусы,
            8: не индусы
        }
    }
}

Теперь сделаем эффективный алгоритм для взлома паролей:

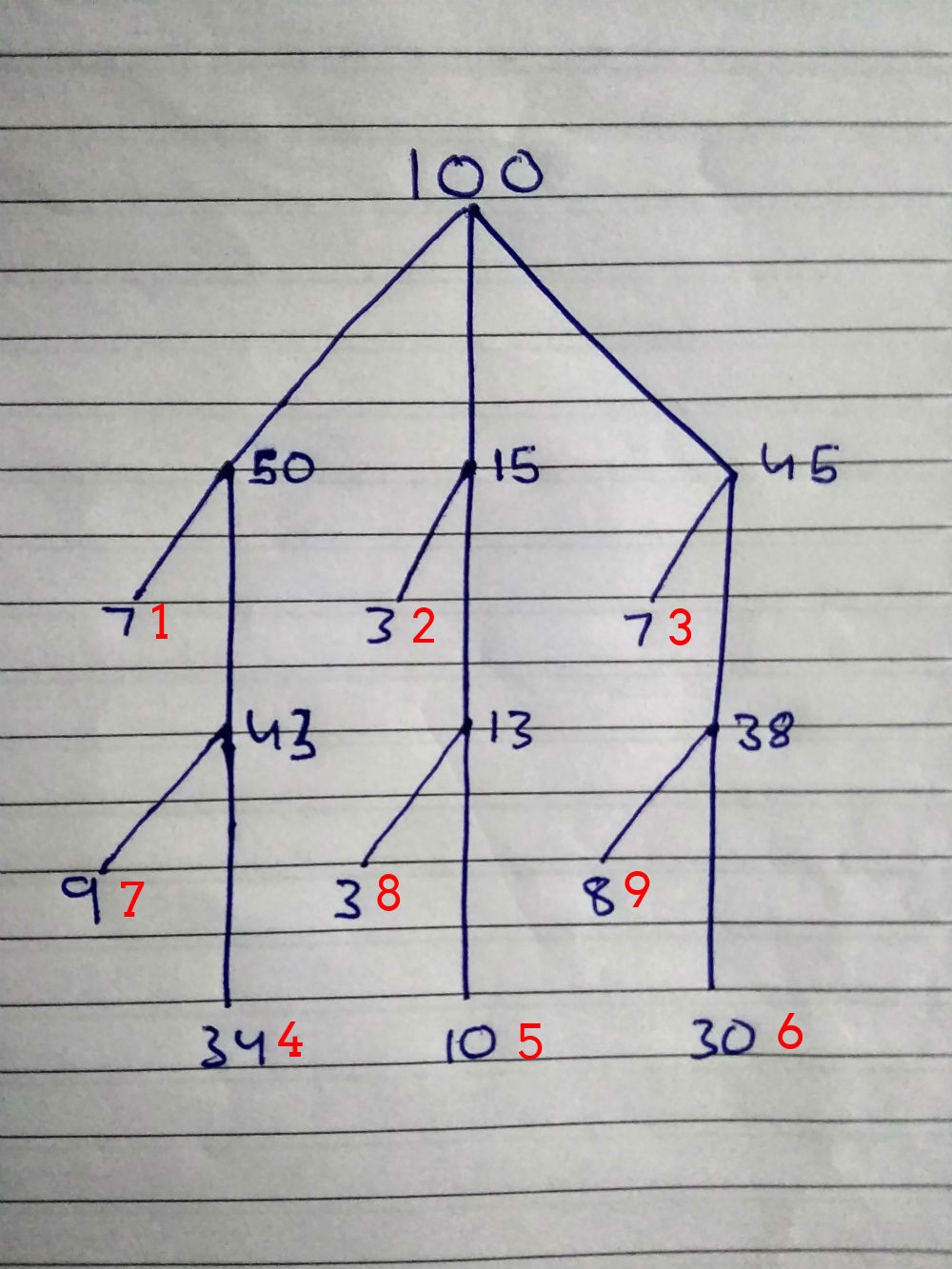
Красные числа — это поисковый приоритет. Комбинации для людей первой группы протестируем первыми, потом вторые, потом третьи и так далее.

Сколько теперь нужно времени для взлома?

Фаза №1
1 = 11 секунд для взлома 7 паролей
2 = 3 секунды для взлома 3 паролей
3 = 11 секунд для взлома 7 паролей

Мы взломали пароли 17 человек, осталось 83. Удалим предыдущие комбинации из списка и будем пробовать следующие наборы — 4, 5, 6.

Фаза №2
4 = 54 секунды для взлома 34 паролей
5 = 16 секунд для взлома 10 паролей
6 = 47 секунд для взлома 30 паролей

Снова удаляем комбинации предыдущих фаз.

Фаза №3
7 = 14 секунд для взлома 9 паролей
8 = 5 секунд для взлома 3 паролей
9 = 12 секунд для взлома 8 паролей

Суммарное время: секунды или 2 минуты и 13 секунд.

Взломанных паролей: 100

Среднее время для одного пароля: секунды.

92 года → 1.73 секунды. Ниче так, да?

Автор: atamanenko

Источник