В одном из проектов, над которыми мне довелось работать, был реализован механизм обмена данными между удалёнными компонентами системы, работавший по следующему сценарию: компонент-источник А на своей стороне подготавливает данные, предназначенные для передачи; компонент-получатель Б периодически открывает сеанс связи и забирает все данные, которые накопил А на момент подключения. Данные, поступающие уже в во время сеанса связи, откладываются до следующего подключения.
В какой-то момент я понял, что передача данных в такой схеме описывается с помощью обыкновенного дифференциального уравнения. Описание модели и выводы, которые удалось получить с её помощью, под катом.
Обозначим 






Если скорость накопления данных на стороне А обозначить 

Так как неограниченный рост объёма ещё непереданных данных является крайне нежелательной ситуацией, то важной задачей становится получение условий ограниченности решений этого уравнения.
Для простоты будем считать функцию 
где
при всех 

Рассмотрим несколько примеров. Пусть 
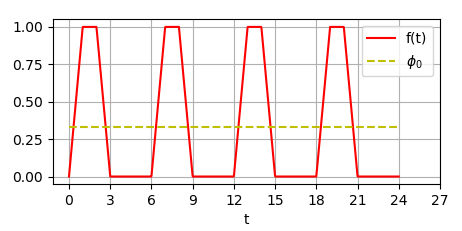
В этом случае 

Численно проинтегрировав уравнение (1) для нескольких значений параметров 

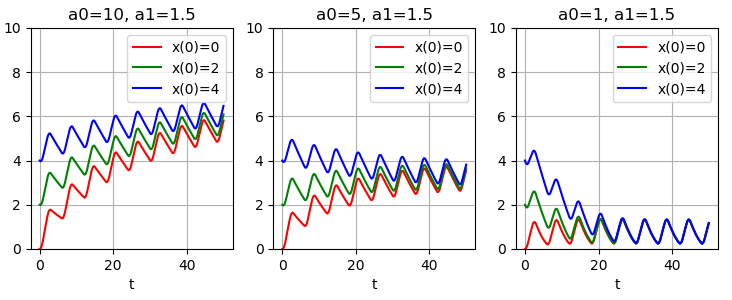
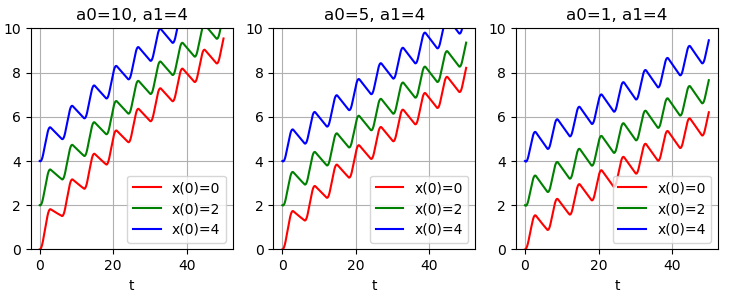
Из примеров видно: когда 




В общем случае можно показать, что если 


В итоге анализ модели позволяет сделать следующие выводы. Если скорость обмена оказывается недостаточной, и на стороне источника постоянно растёт объём данных для отправки, то пытаться исправить ситуацию уменьшением пауз между сеансами не имеет смысла. Помочь здесь может только увеличение производительности системы.
С другой стороны, в случае когда сервис обмена постоянно загружает компьютеры в ущерб другим задачам, верным решением будет рекомендовать увеличить в разумных пределах продолжительность пауз: это повлияет только актуальность данных, без риска переполнения источника неотправленными данными.
Подробные выкладки для условий ограниченности решений и некоторые другие вопросы, касающиеся рассмотренной модели, опубликованы в материалах школы-семинара ”Математическое моделирование, численные методы и комплексы программ” имени Е.В. Воскресенского. Посмотреть и скачать статью можно по этой ссылке.
Автор: Дмитрий Пашуткин







