Идея этого алгоритма пришла мне в голову ещё в 2006 на лекции по криптографии, как раз посвящённой алгоритму RSA. На ней говорилось, что большое число x из диапазона 22000÷24000 считается простым если удовлетворяет неким критерии простоты и если остальные числа в его окрестностях (x-2000;x) являются составными. Тогда меня удивило, зачем проверять все ближайшие числа на простоту, если можно специально выбирать числа, рядом с которыми в заданном диапазоне все соседи являются составными по-умолчанию? Алгоритм был придуман, описан и опубликован в университетском сборнике, но т.к. их никто не читает, то опубликую его здесь. Авось, кому-то пригодится;)
Но для начала напомню один из распространённых способов отсеивания большинства составных чисел, использующийся при поиске больших простых чисел:
"Решето" (sieve).
Идея в следующем: делим тестируемое число p на сотню первых простых чисел. Если делится (остаток от деления равен нулю) — число составное.
На самом деле, конечно, никто не будет постоянно делить большое число на сотню простых, это очень долго. Поэтому производится следующая оптимизация: составляется таблица остатков remainder[] от деления начального значения тестируемого числа p на нашу сотню простых чисел prime[]. Затем, при поиске простого числа, вместе с самим числом p увеличивается некоторое дельта-значение pdelta. И при поиске остатка от деления p на i-е простое число prime[i] вместо p в качестве делимого берется сумма pdelta+remainder[i]. То есть, используется равенство
p % prime[i] = (pdelta + remainder[i]) % prime[i].
Моя задача заключалась в разработке математического алгоритма для поиска некоторых двух чисел X1, X2 в диапазоне 22000÷24000, о которых можно с большой вероятностью сказать, что они являются простыми, а также что числа на промежутке [X1-2000; X1)U(X1; X2)U(X2; X2+2000] — являются составными.
Большая вероятность обусловлена тем, что простые числа распределены на числовой оси относительно равномерно, хотя с ростом разрядности их плотность уменьшается.
Теорема 1.
Формулировка:
Если для любого составного числа известно некоторое конечное множество его простых делителей, то число, предыдущее ему, и число, за ним следующее, не кратны ни одному из простых делителей из этого множества.
Доказательство:
Пусть X – конечное множество известных простых делителей числа n(по условию единица не является простым числом);
X = [x1,x2,..,xk,..,xn]
n+ и n- это числа (n+1) и (n-1) соответственно.
Покажем, что числа n+ и n- не кратны ни одному из простых делителей из множества X.
Доказательство ведем от противного:
Предположим, что число n и числа n± имеют общий множитель xk.
Тогд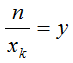а 
, а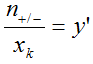 
соответственно.
Из условия, что n и n± делятся нацело на xk, получаем: |y-y'| ≥ 1.
Подставим сюда выражения для y и y’:
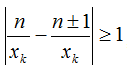
Приведем подмодульное выражение к общему знаменателю и получим, что 1 / xk ≥ 1 или xk ≤ 1, чего быть не может, так как все xk – натуральные числа не равные единице.
Теорема доказана.
Теорема 2.
Формулировка: Для составного числа n, в разложении которого на сомножители присутствуют все простые числа из диапазона [2; a], о всех числах в промежутке n±a, кроме n±1, можно точно сказать, что они не являются простыми.
Доказательство:
Пусть Y – множество чисел, соответствующее промежутку [2; a];
Пусть X – множество всех простых чисел, входящих в промежуток [2; a];
Тогда Y’ – множество всех чисел, входящих в промежуток [2; a], за исключением чисел, составляющих множество Х.
Пусть число n в разложении содержит все простые числа множества X (кроме того оно может содержать произвольное число любых других множителей, не принадлежащих множеству X; на доказательстве теоремы это никак не отразится).
Произведение, не входящих во множество X множителей, условно обозначим как П.
Тогда n имеет вид: n = x1×x2×..×xk×..×xa×П.
Каждое число nj из промежутка n±a мы сможем представить в виде:
nj = x1×x2×..×xk×..×xa×П±yj, где yj – число из множества Y.
Легко увидеть, что если yj принадлежит X, т.е. yj=xk, то:
nj = x1×x2×..×xk×..×xa×П±xk = xk(x1×x2×..×xk×..×xa×П±1) и nj кратно xk.
В противном случае, yj принадлежит y’k, т.е. является составным и может быть представлено в виде произведения конечного числа простых чисел из того же подмножества X, т. о. мы сможем всегда выделить общий множитель в выражении вида:
nj = x1×x2×..×xk×..×xa×П±y'j.
Следовательно, получаем, что все числа в промежутке n±a, кроме n±1 (принимая во внимание теорему 1), являются составными.
Теорема доказана.
Суть алгоритма
Чтобы воспользоваться доказанными выше теоремами, для вычисления числа мы будем использовать все простые множители из диапазона Y=[2;2000]. Произведение всех простых чисел из диапазона [2;2000] равно
9397902846655662330092838642686864126551788576177450069985416980084068530565057190532639389114744350352
2793860584071591452879655775734323993447280229950516208168456242859704539545043029470723016883062129865
1889833074457599441317875637777522365340428387365718257681473098758795686487618484924746922690757379938
2051096884705979775013773857968058350704148768501714952462791606364437508606899949529898134977654032079
6738483271972712449573928869390146878678278551706732964746955815021418849063826580384371871911662113251
2884245970190515058116574554626291842232351682026357515627185226065166986223960251188849343993261790060
9311758000459181619937785387630516653871526948649691396533829901864156371841265520699316641510940580287
7992948356769154670
Затем это число домножается до заданной разрядности (в своей реализации оно домножается в случайном порядке простыми числами из диапазона [2; 10000]).
Искомое n будет делиться на все числа из Y, поэтому мы можем применить к нему теорему 2 и показать, что все числа из промежутка n±2000, кроме n±1, будут составными.
Пользуясь теоремой 1 можно показать, что n±1, по крайней мере, не делятся ни на одно простое число, принадлежащее промежутку Y.
Полученную пару чисел можно также проверить на простоту с помощью других критериев.
Автор: malan
