Предыстория
Некоторое время назад я сделал обратный маятник. После нескольких итераций с шаговыми моторами равновесия достичь не удалось. Тогда у меня было мало опыта и понимания проблемы, поэтому я переделал его с мотором постоянного тока, как большинство учебных проектов. Однако, встречаются статьи о том, как сделать балансирующего робота на шаговых моторах. По сути это одна и та же задача, поэтому я к ней решил вернуться и разобраться с прошлых неудачах. Ниже я опишу все, что нужно знать, чтобы сделать своего робота, и трудности, с которыми столкнулся.
Постановка задачи
Сделать балансирующего робота из доступных компонентов с возможностью управления и дальнейшего расширения как платформы.
Используемое железо:
-
Arduino Nano (Keywish BLE-Nano) последовательный порт аппаратно проброшен через Bluetooth, что устраняет расходы процессора на коммуникацию. Можно использовать классический контроллер Arduino Nano, код совместим, но не будет управления
-
MPU6050 - популярный инерциальный модуль для определения угла наклона робота
-
A4988 x2 - драйверы шаговых моторов
-
Nema17 motor x2 - шаговые моторы
Цена компонентов: ~75$
В чем привлекательность использования шаговых моторов? В задачах удержания равновесия нужно создавать силу, действующую на тело робота или стержень, в случае обратного маятника. Значит, нужно управлять угловым ускорением вала. В случае с шаговыми моторами это можно сделать программно, без обратной связи, если предположить, что двигатель не пропускает шаги. Однако, тут важно своевременно формировать импульсы на шаг. Об этом речь пойдет ниже. В случае с коллекторным мотором нужен энкодер для обратной связи и контур управления моментом.
Мат. модель
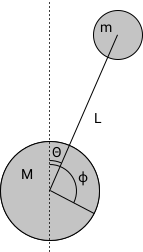
Движение робота описывается следующими уравнениями:
где R - радиус колеса; I = 1/2*M*R^2 - момент инерции колеса; b1 - трение в оси колеса; b2 - трение качения.
Моделирование с разными способами управления приводится здесь. Так, например, выглядит свободная модель без трения и управления, и со стабилизацией.
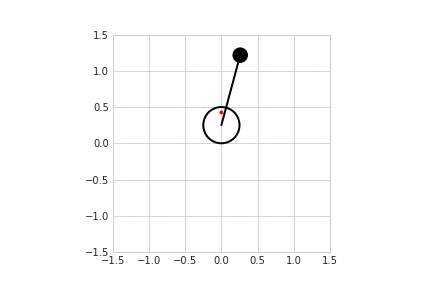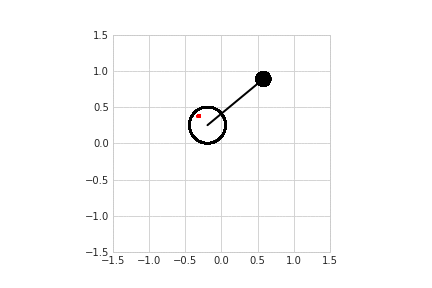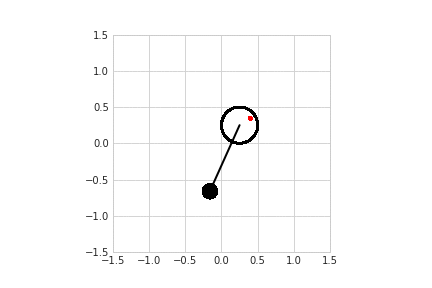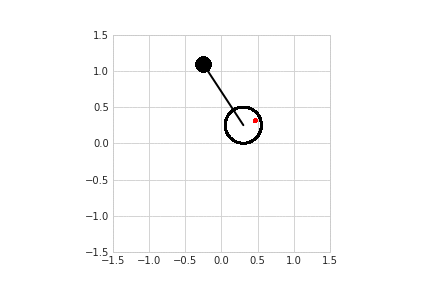
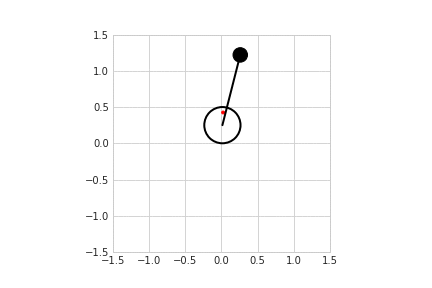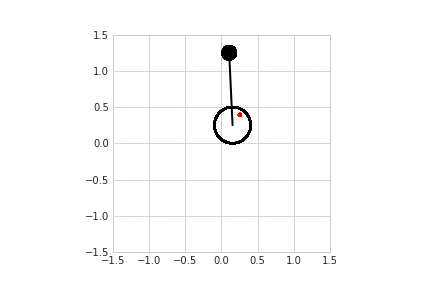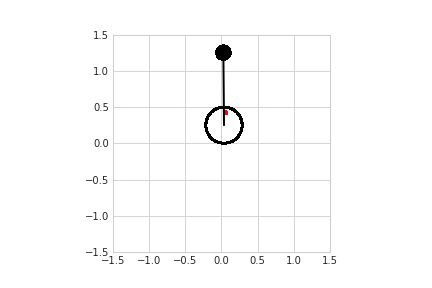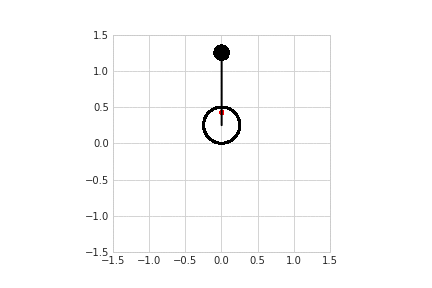
Алгоритм стабилизации
Для удержания равновесия нужна обратная связь по углу, а чтобы робот не уехал со стола в процессе отладки, нужно занулить скорость, поэтому схема выглядит так:
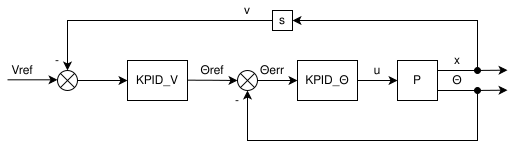
Контур скорости задает желаемый угол, а внутренний контур его достигает. В реальности координата X не измеряется, в ходе вычислений уже есть скорость V, которую, как предполагается, шаговый мотор точно выдает.
Управление скоростью
Управление скоростью автоматически получилось по схеме выше: чтобы заставить робот ехать вперед или назад, нужно задать входную скорость.
Но как быть с поворотом? Если добавить константу скорости прямо на двигатель, это не повлияет на равновесие, т.к. ускорение не изменится. Предполагается, что скорость, которую задает пользователь, изменяется гораздо медленее, чем реагирует робот на изменение угла. Тогда для поворота можно добавить скорость к одному двигателю и вычесть у другого. Стоит обратить внимание на насыщение мотора, если поворачивать очень быстро, то при попытке балансировать скорости на одном колесе сложатся, момент упадет, и двигатель начнет пропускать шаги; либо контроллер не будет успевать генерировать импульсы с достаточной частотой.
Сложности реализации
Управлять шаговым мотором просто, когда скорость не критична. В данном случае, нужно управлять ускорением, поэтому следует учесть два параллельных процесса: подача импульсов для шага и пересчет задержки между шагами.
Оценим требуемую частоту импульсов на шаг. Пусть максимальная скорость - 1 оборот в секунду (при колесе от роликов диаметром 72мм, ~22 см/с), двигатель настроен в режиме 1/8 шага, 1600 импульсов на оборот, значит, как минимум процесс, отправляющий импульсы на шаг должен работать с частотой 1.6kHz, причем время должно выдерживаться точно, значит, нужно использовать прерывания по таймеру. Но достаточно ли этого?
Здесь возникает понятие - разрешение (resolution) по скорости, т.е. насколько малые приращения по скорости контроллер способен выдать. Задержка между шагами - это целое количество прерываний таймера (1.6kHz, 800Hz, 533Hz, 400Hz, ...) Программой ниже можно оценить насколько точно можно аппроксимировать желаемые изменения скорости в зависимости от частоты прерываний.
Код
import numpy as np
import matplotlib.pyplot as plt
from math import pi
PULSES_PER_REVOLUTION = 1600
def get_physical_velocity(velocity, frequency):
ticks_per_pulse = round(2.0 * pi * frequency / (velocity * PULSES_PER_REVOLUTION))
return 2.0 * pi * frequency / (ticks_per_pulse * PULSES_PER_REVOLUTION)
times = np.linspace(0, pi, 1000)
velocities = np.sin(times)
physical_velocities = list(map(lambda x: get_physical_velocity(x, 1600), velocities))
physical_velocities_2 = list(map(lambda x: get_physical_velocity(x, 50000), velocities))
plt.plot(times, velocities)
slow_label, = plt.plot(times, physical_velocities, label="1.6kHz")
fast_label, = plt.plot(times, physical_velocities_2, label="50kHz")
plt.legend([slow_label, fast_label], ['1.6kHz', '50kHz'])
plt.grid(True)
plt.show()
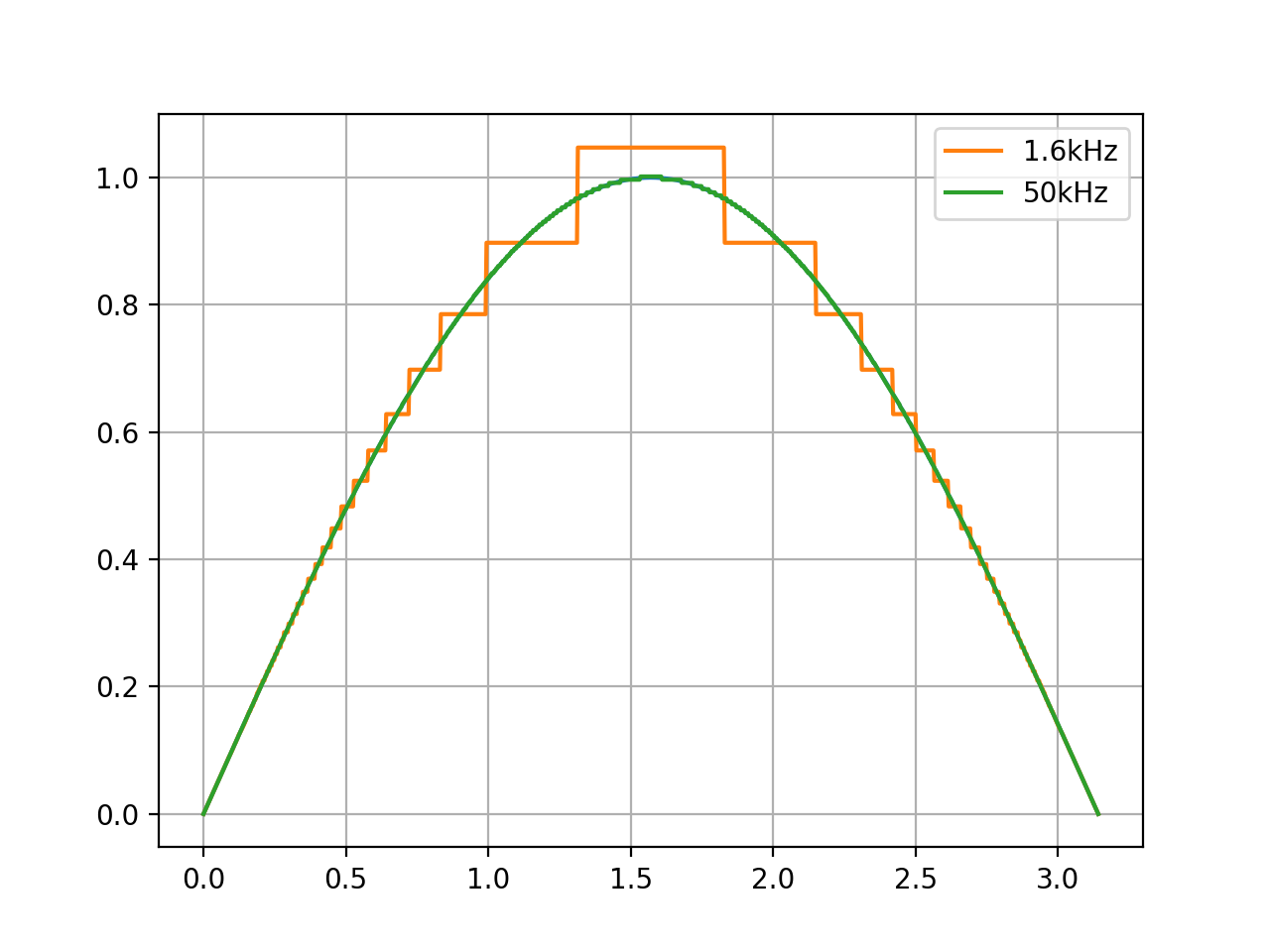
тоесть, чем ниже частота, тем хуже можно аппроксимировать скорость в области высоких скоростей, что для робота будет равносильно удару. Я использовал 50kHz. Стоит помнить, что чем выше частота прерываний таймера, тем медленнее работает основной цикл.
Второй процесс - рассчет задержки между шагами, в идеальном случае, если робот движется с ускорением, то после каждого шага нужно пересчитать задержку до следующего шага, т.е. это было бы правильно делать прямо в обработчике прерывания таймера, но формула содержит деление ticks_per_pulse = round(2.0 * pi * frequency / (velocity * PULSES_PER_REVOLUTION)), и обработчик может не успеть закончить работу до наступления след. прерывания. Поэтому задержка пересчитывается в основном цикле как можно чаще.
Несколько советов, как ускорить программу:
-
Wire.setClock(1000000UL);- ускоряем коммуникацию с MPU6050 -
Использовать DMP (Digital Motion Processor) встроенный в MPU6050, а не реализовывать комплиментарный фильтр или фильтр Калмана, это дало ускорение обработки основного цикла в 5 раз (2.5kHz)
-
Использовать пин прерывания на IMU и читать данные только тогда, когда закончена обработка, чтобы не опрашивать его постоянно, это ускорило основной цикл еще в 8 раз до 19kHz
-
не забыть откалибровать IMU, иначе измерения угла все время будут плыть.
Код проекта доступен здесь.
Схема
Ниже схема, по которой я заказал печатную плату в JLPCB. Хотелось бы получить обратную связь от опытных схемотехников, особенно по части разведения питания.
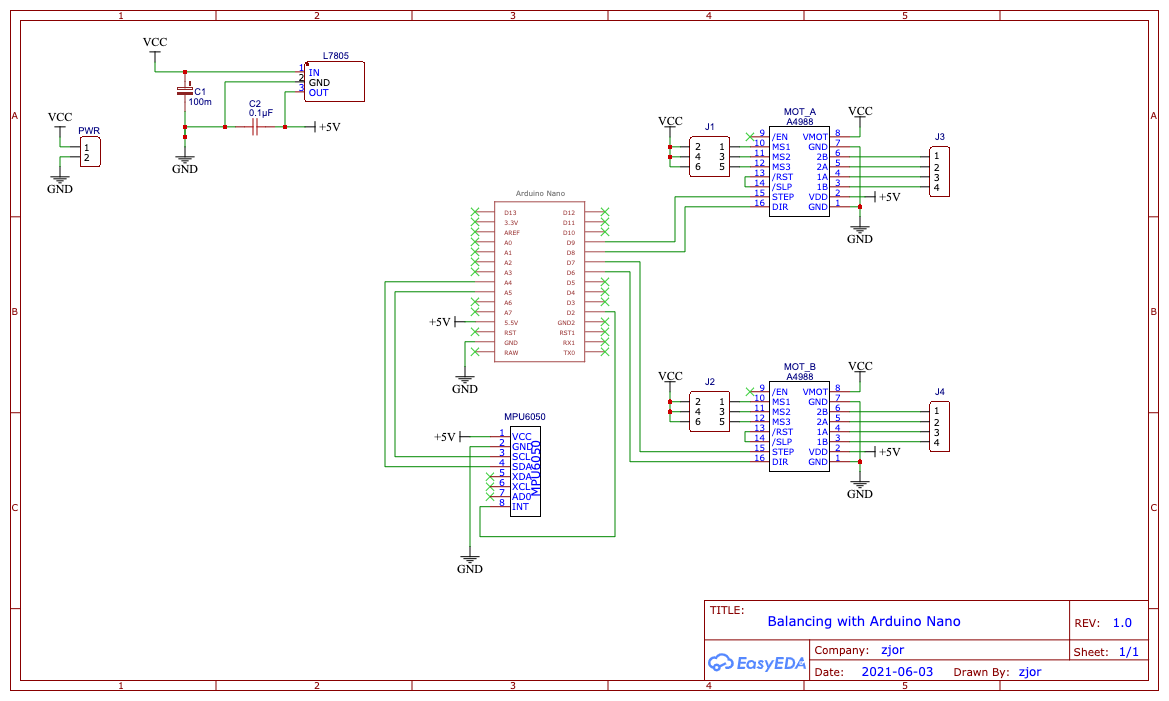
Результат
Т.к. в BLE-Nano встроен Bluetooth, и не надо писать дополнительный код, легко добавить управление. Я переделал SerialTerminal под Android и сделал из него пульт управления.
План дальнейшего развития:
-
Сделать расширяемую платформу (другой контроллер или Raspberry будет делать всю высокоуровневую работу, а Nano будет предоставлять API по настройке и управлению)
-
Добавить сенсоры (препятствий, линии под роботом, микрофон, камеру)
-
Добавить индикаторы (заряда батареи, угла, скорости)
-
Присоединить телефон и установить конференц-связь
Буду рад, если кто-то захочет присоединиться.
Ссылки
Автор: Сергей






