Сегодня я хотел бы поднять тему, которая в последнее время становится всё актуальней и интересней. По крайней мере, судя по всё увеличивающемуся количеству публикаций в этому направлении, интерес к ней действительно растёт. Речь веду о так называемых квантовых вычислениях, или, если точнее, о модели квантовых вычислений. Не вдаваясь в самую суть этой модели, я предлагаю уважаемым читателям рассмотреть один из многочисленных вопросов, который имеется в рамках обозначенной темы. Речь поведём об обратимых вычислениях.
Дальнейшее изложение будет проводиться с использованием многочисленных примеров на языке программирования Haskell. Дело в том, что по моему сугубому мнению, функциональное программирование находится намного ближе к модели квантовых вычислений, чем любой иной тип. Обосновывать эту точку зрения я сейчас не буду. Но суть в ином — для постижения модели квантовых вычислений нужен намного более суровый сдвиг парадигмы, чем, к примеру, такой сдвиг от структурного программирования к объектно-ориентированному и тем более к функциональному. Здесь нет ни слова о том, что кто-то из программистов находится выше или ниже, но лишь о том, что освоение новой модели — это реальный переворот в мозгах и способе алгоритмического .
Так что если вам интересна тема, и вы хотите немного погрузиться в волшебный мир квантовых вычислений, то предлагаю ознакомиться с этой небольшой заметкой. Ну а в конце всех ждёт пятничный бонус.
Необходимые исторические сведения
Если обратить своё пристальное внимание на элементы булевой алгебры, то мы увидим, что все элементы на два входа и один выход в процессе своей работы теряют информацию. Например, булева функция И, таблица истинности которой следующая:
| X | Y | X & Y |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
неизбежно теряет информацию о значении входных битов. Действительно, если мы на выходе имеем значение 0, то понять, на каких именно входных значениях получен этот результат мы не сможем.
Рольф Ландауэр впервые задумался об этом аспекте вычислений в 1961 году, и из его размышлений родился принцип, который связывает информационную энтропию с энтропией термодинамической. Действительно, потеря информации связана с выделением тепла физическими вычислительными устройствами.
А что если реализовать такие вычислительные элементы, при работе которых не теряется информация? С точки зрения чистой (теоретической) логики в этом нет ничего сложного. Проблема заключена в ином — нужны такие элементы, при помощи которых можно было бы реализовать любую иную булеву функцию. На как, например, базис из стандартных элементов НЕ и ИЛИ, или одноэлементный базис И-НЕ.
Обратимые элементы с этим свойством были найдены. В этой статье мы рассмотрим пару таких элементов — элемент Тоффоли и элемент Фредкина.
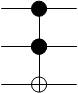
Элемент Тоффоли
Логический элемент Тоффоли представляет собой булеву функцию, получающую на вход три бита и возвращающую три бита (то есть это функция типа f: {0, 1}3 → {0, 1}3). Её таблица истинности выглядит следующим образом:
| Вход | Выход | ||||
| C1 | C2 | I | C1 | C2 | O = I ⊕ C1C2 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 0 |
Другое название этой функции — CCNOT, то есть Controlled-Controlled-NOT. Это название учитывает тот факт, что логическая функция НЕ применяется к третьему биту I тогда и только тогда, когда первые два бита имеют значение 1. Данная прекрасная функция не просто является обратимой (если присмотреться, то будет видно, что между входными и выходными тройками значений есть взаимно однозначное отображение), но и она одна может использоваться для выражения любой иной булевой функции. Доказательство этого факта простое — если зафиксировать значение входного бита I в 1, то функция представит собой элемент И-НЕ, который является базисным.
Давайте попробуем посмотреть это в деле. Реализуем определение элемента Тоффоли на языке Haskell. Вместе с тремя дополнительными сервисными функциями определение функции toffoli будет выглядеть следующим образом:
getX :: (Int, Int, Int) -> Int
getX (x, _, _) = x
getY :: (Int, Int, Int) -> Int
getY (_, y, _) = y
getZ :: (Int, Int, Int) -> Int
getZ (_, _, z) = z
toffoli :: Int -> Int -> Int -> (Int, Int, Int)
toffoli 1 1 0 = (1, 1, 1)
toffoli 1 1 1 = (1, 1, 0)
toffoli x y z = (x, y, z)
Здесь есть очень сильные упрощения:
- Во-первых, для представления значений битов использован тип
Int, что не совсем корректно. Лучше было бы использовать, хотя бы, типBool, а ещё лучше определить свой собственный тип-перечисление для этих целей. Но это было бы слишком громоздко для демонстрации. Здесь мы просто посмотрим на реализацию, и всё. - Из предыдущего упрощения следует то, что разработчику следует самостоятельно следить за корректностью значений. В эти функции вполне можно подать значения 2 и другие, не равные 0 или 1, и функции успешно отработают с точки зрения компилятора. Но мы не будем подавать такие значения, поскольку они выходят за область нашего рассмотрения — сейчас из всех целых чисел нас интересуют только 0 и 1.
- Функция
toffoliвозвращает тройку, и это самый простой способ вернуть три значения в языке Haskell. В принципе, для этих целей можно было бы определить специальный тип, но для упрощения пусть будет так. И именно этим фактом вызвано определение сервисных функцийgetX,getYиgetZ.
Теперь выразим через элемент Тоффоли все основные логические операции: отрицание (НЕ), конъюнкция (И), дизъюнкция (ИЛИ), И-НЕ, ИЛИ-НЕ, исключающее ИЛИ и дублирование бита. Необходимо отметить, что последняя операция всегда присутствует в логике, но она вводится там совершенно неявно, а на логических схемах обозначается просто разветвлением «провода», обозначающего бит.
Итак, вот определения функций:
not :: Int -> Int
not = getZ . toffoli 1 1
and :: Int -> Int -> Int
and a b = getZ $ toffoli a b 0
nand :: Int -> Int -> Int
nand a b = getZ $ toffoli a b 1
or :: Int -> Int -> Int
or a b = not $ and (not a) (not b)
nor :: Int -> Int -> Int
nor a b = not $ or a b
xor :: Int -> Int -> Int
xor a b = getZ $ toffoli 1 a b
fanout :: Int -> (Int, Int)
fanout a = (getY t, getZ t)
where
t = toffoli 1 a 0
Необходимость операции дублирования бита, выраженной через обратимый элемент Тоффоли, совершенно обоснованна, поскольку в обычной логике эта операция необратима. А в квантовых вычислениях так просто разветвлять «провода» кубитов нельзя, поскольку это запрещает делать теорема о невозможности копирования квантового состояния.
То, что в вышеприведённом коде некоторые функции выражены не прямо через функцию toffoli, не обозначает, что мы не можем их выразить. Да, через один элемент Тоффоли не получается, но приходится через несколько — и для сокращения записи нам помогают уже определённые функции.
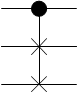
Элемент Фредкина
Теперь перейдём к ещё одному элементу обратимой логики, который как и элемент Тоффоли является во-первых обратимым, а во-вторых базисным, то есть через него можно выразить любую иную логическую функцию. Тип функции, представленной элементов Фредкина, абсолютно такой же, как и у элемента Тоффоли, то есть она принимает на вход три биты, и три бита же и возвращает. Таблица истинности этого элемента следующая:
| Вход | Выход | ||||
| C | I1 | I2 | C | O1 | O2 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 |
Этот элемент ещё называется CSWAP, то есть Controlled-SWAP. Эта функция обменивает значения входных битов I1и I2 тогда и только тогда, когда значение контролирующего бита C равно 1. При помощи этого элемента тривиальным образом кодируются операции булевой логики НЕ и И, а потому он является базисным. Собственно, вот так кодируются при помощи него все те же самые функции, которые были выражены ранее через функцию toffoli:
not' :: Int -> Int
not' a = getZ $ fredkin a 0 1
and' :: Int -> Int -> Int
and' a b = getZ $ fredkin a b 0
nand' :: Int -> Int -> Int
nand' a b = not' $ and' a b
or' :: Int -> Int -> Int
or' a b = not' $ and' (not' a) (not' b)
nor' :: Int -> Int -> Int
nor' a b = not' $ or' a b
xor' :: Int -> Int -> Int
xor' a b = or' (and' b $ not' a) (and' a $ not' b)
fanout' :: Int -> (Int, Int)
fanout' a = (getX f, getZ f)
where
f = fredkin a 1 0
К этому коду относятся те же самые соображения, что и к предыдущему — выражение функций через уже определённые не влияет на то, что все они выражены через элемент Фредкина.
Также тут надо отметить, что сами функции toffoli и fredkin являются обратимыми, а вот остальные функции, которые через них выражены, — уже нет. Почему? Да потому, что сервисные функции getX, getY и getZ теряют информацию, и они специально сделаны такими.
Выражение одного через другое
Теперь займёмся упражнениями более высокого порядка. Выразим-ка элемент Тоффоли через элемент Фредкина и наоборот. Это будет хорошим упражнением.
Выразить элемент Тоффоли — в этом нет ничего сложного, поскольку два первых входа не изменяются, а для третьего есть простейшая пропозиционная формула: O = I ⊕ C1C2. Так что определение будет таким:
toffoli' :: Int -> Int -> Int -> (Int, Int, Int)
toffoli' x y z = (x, y, xor' z $ and' x y)
Ради такого дела я даже нарисовал диаграмму, которая показывает всю прелесть выражения одного элемента через другой. Вот она:
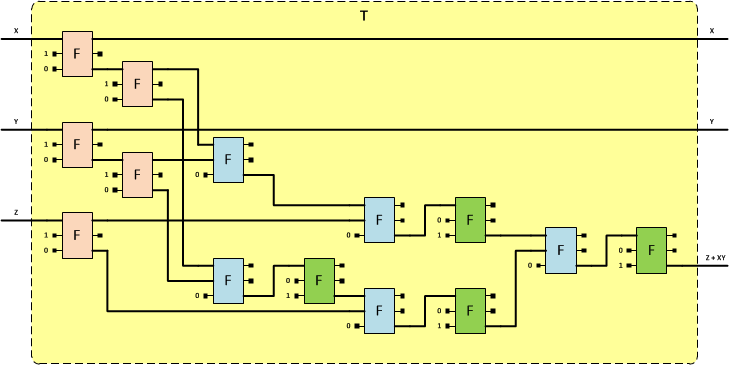
Эта диаграмма показывает, что для выражения одного элемента Тоффоли, у которого три входа и три выхода, при помощи элемента Фредкина, оных элементов необходимо: 5 для выражения операции FANOUT (дублирование значения бита; красные прямоугольники F), 5 для операции И (синие прямоугольники F) и 4 для операции НЕ (зелёные прямоугольники F) — всего 14 элементов, которые в общем представляют 26 входов и выходов, из которых только по 3 являются значимыми. То есть 23 бита являются «мусорными», которые нужны лишь для обеспечения обратимости вычислений.
Это, в свою очередь, обозначает, что при конструировании схем обратимых вычислений мы непременно сталкиваемся с увеличением (экспоненциальным?) размеров вычислительных схем, и, как следствие, с необходимостью увеличения памяти для выполнения таких вычислений. Это плата за обратимость. Так что вопрос для обсуждения — не станет ли преградой для квантовых вычислений необходимость экспоненциального наращивания памяти?
А вот выражение элемента Фредкина через элемент Тоффоли будет посложнее, поскольку у него два выходных бита, которые имеют более сложные пропозиционные формулы. Но тоже не ахти как сложно:
fredkin' :: Int -> Int -> Int -> (Int, Int, Int)
fredkin' x y z = (x, xor y s, xor z s)
where
s = and x $ xor y z
Заинтересованный читатель сможет попробовать нарисовать такую же приятную для взора диаграмму и посчитать на ней количество элементов Тоффоли и «мусорных» битов.
Вот и вся наука.
Пятничный бонус
Поскольку у нас сегодня пятница, вот вам, мои уважаемые читатели, небольшой бонус. Поразмышляем насчёт многострадального кота Шрёдингера. Вот я всегда думал, почему Эрвин Шрёдингер не смог объяснить свой «парадокс». Он же сам написал книгу «Что такое жизнь с точки зрения физики».
Весь вопрос в восприятии. Только живое существо может воспринимать (даже амёба). А восприятие — это акт измерения, которое разрушает суперпозицию. Так что поместив в ящик кота, Шрёдингер сам посадил в ящик «средство измерения». Фотон, находясь в суперпозиции квантовых состояний после преодоления полупрозрачного зеркала, входит в таком состоянии в ящик и детектор. Но тут же система восприятия кота разрушает суперпозицию. И дело не в сознании, а именно в восприятии.
Когда у нас есть фотон в суперпозиции, и он попадает в некое измерительное устройство (не живое, а просто измерительное устройство), то и само устройство, хоть и является макрообъектом, входит в суперпозицию состояний «фотон засечён» — «фотон не засечён». Впрочем, возможно, я ошибаюсь. Эксперименты по проверке этого парадокса запланированы Роджером Пенроузом (я не в курсе, удалось ему их провести или нет), но он не будет сажать котов в коробки, это уж точно.
Или что это? Проблема Наблюдателя?
Автор: Darkus
