Вместо введения
В статье описывается исследование, проведенное с целью проверки утверждения центральной предельной теоремы о том, что сумма N независимых и одинаково распределенных случайных величин, отобранных практически из любого распределения, имеет распределение, близкое к нормальному. Однако, прежде чем мы перейдем к описанию исследования и более подробному раскрытию смысла центральной предельной теоремы, не лишним будет сообщить, зачем вообще проводилось исследование и кому может быть полезна статья.
В первую очередь, статья может быть полезна всем начинающим постигать основы машинного обучения, в особенности если уважаемый читатель еще и на первом курсе специализации «Машинное обучение и анализ данных». Именно подобного рода исследование требуется провести на заключительной неделе первого курса, указанной выше специализации, чтобы получить заветный сертификат.
Подход к проведению исследования
Итак, вернемся к вопросу исследования. О чем говорит нам центральная предельная теорема. А говорит она вот о чем. Если есть случайная величина X из практически любого распределения, и из этого распределения случайным образом сформирована выборка объемом N, то выборочное среднее, определенное на основании выборки, можно приблизить нормальным распределением со средним значением, которое совпадает с математическим ожиданием исходной совокупности.
Для проведения эксперимента нам потребуется выбрать распределение, из которого случайным образом будет формироваться выборка. В нашем случае мы воспользуемся экспоненциальным распределением.
Итак, мы знаем, что плотность вероятности экспоненциального распределения случайной величины X имеет вид:
$$display$$f(x) = lambda varepsilon^{-lambda x}$$display$$
, где $inline$x > 0$inline$, $inline$lambda>0$inline$
Математическое ожидание случайной величины X, в соответствии с законом экспоненциального распределения определяется, обратно $inline$lambda$inline$: $inline$mu = frac{1}{lambda}$inline$
Дисперсия случайной величины X определяется как $inline$sigma^2 = frac{1}{lambda^2}$inline$
В нашем исследовании используется параметр экспоненциального распределения $inline$lambda = 0.0125$inline$, тогда $inline$mu = 80$inline$, $inline$sigma^2 = 6400$inline$
Для упрощения восприятия значений и самого эксперимента, предположим, что речь идет о работе устройства со средним ожиданием времени безотказной работы в 80 часов. Тогда, чем больше времени проработает устройство, тем меньше вероятности того, что не будет отказа и наоборот – при стремлении работы устройства к нулю времени (часам, минутам, секундам), вероятность его поломки также стремится к нулю.
Теперь из экспоненциального распределения с заданным параметром $inline$lambda = 0.0125$inline$ выберем 1000 псевдослучайных значений. Сравним полученные результаты выборки с теоретической плотностью вероятности.
Далее, и это самое главное в нашем небольшом исследовании, сформируем следующие выборки. Возьмем 3, 15, 50, 100, 150, 300 и 500 случайных величин из экспоненциального распределения, определим для каждого объема (от 3 до 500) среднее арифметическое, повторим 1000 раз. Для каждой выборки построим гистограмму и наложим на нее график плотности соответствующего нормального распределения. Оценим получившиеся параметры выборочного среднего, дисперсии и стандартного отклонения.
На этом можно было бы завершить статью, но есть предложение несколько расширить границы эксперимента. Оценим насколько указанные параметры, при увеличении объема выборки от 3 до 500, будут отличаться от своих собратьев – таких же параметров соответствующих нормальных распределений. Другими словами, нам предлагается ответить на вопрос, а будем ли мы наблюдать уменьшение отклонений при увеличении объема выборки?
Итак, в путь. Нашими инструментами сегодня будут язык Python и Jupyter notebook.
Исследуем утверждение центральной предельной теоремы
Исходный код исследования выложен на гитхабе
Внимание! Для работы с файлом требуется Jupyter notebook!
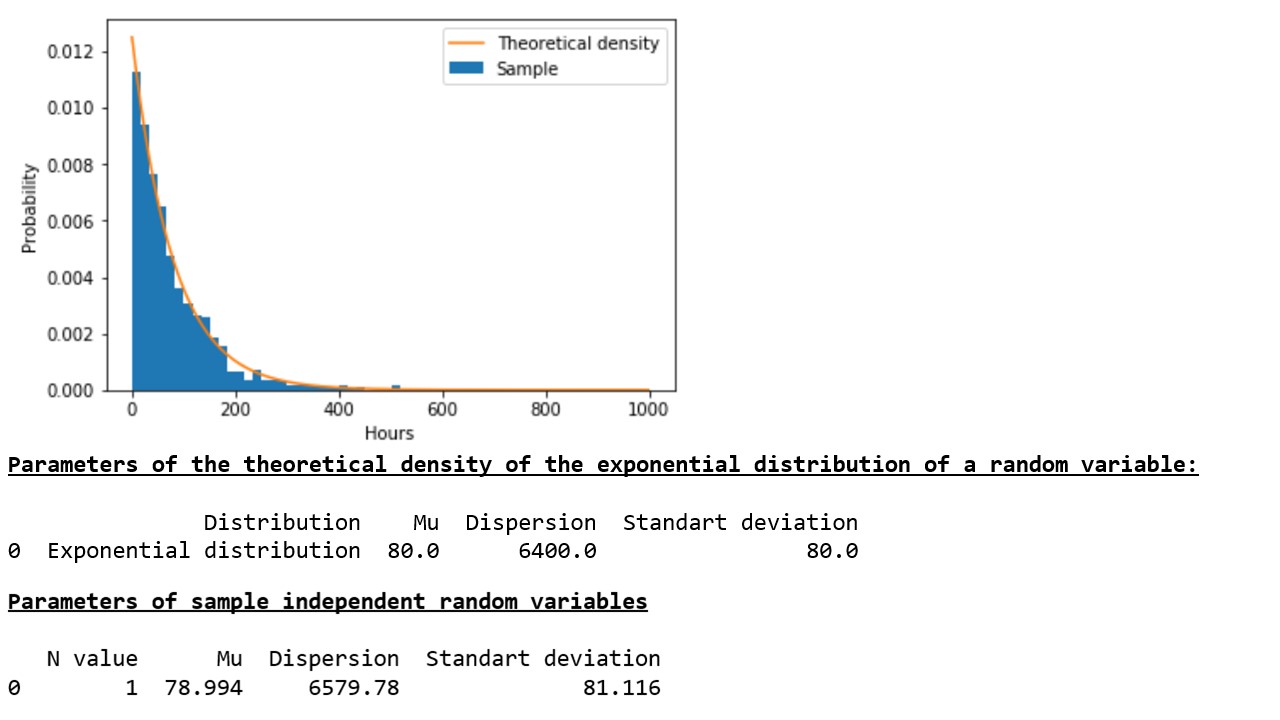
Сгенерированная нами в соответствии с законом экспоненциального распределения выборка псевдослучайной величины 1000 раз достаточно хорошо характеризует теоретическую (исходную) совокупность (график 1*, таблица 1).
График 1, Таблица 1
Теперь посмотрим, что произойдет, если мы возьмем 1000 раз не одну псевдослучайную величину, а среднее арифметическое от 3, 15, 50, 100, 150, 300 или 500 псевдослучайных величин и сравним параметры каждой выборки с параметрами соответствующих нормальных распределений (график 2**, таблица 2).
График 2



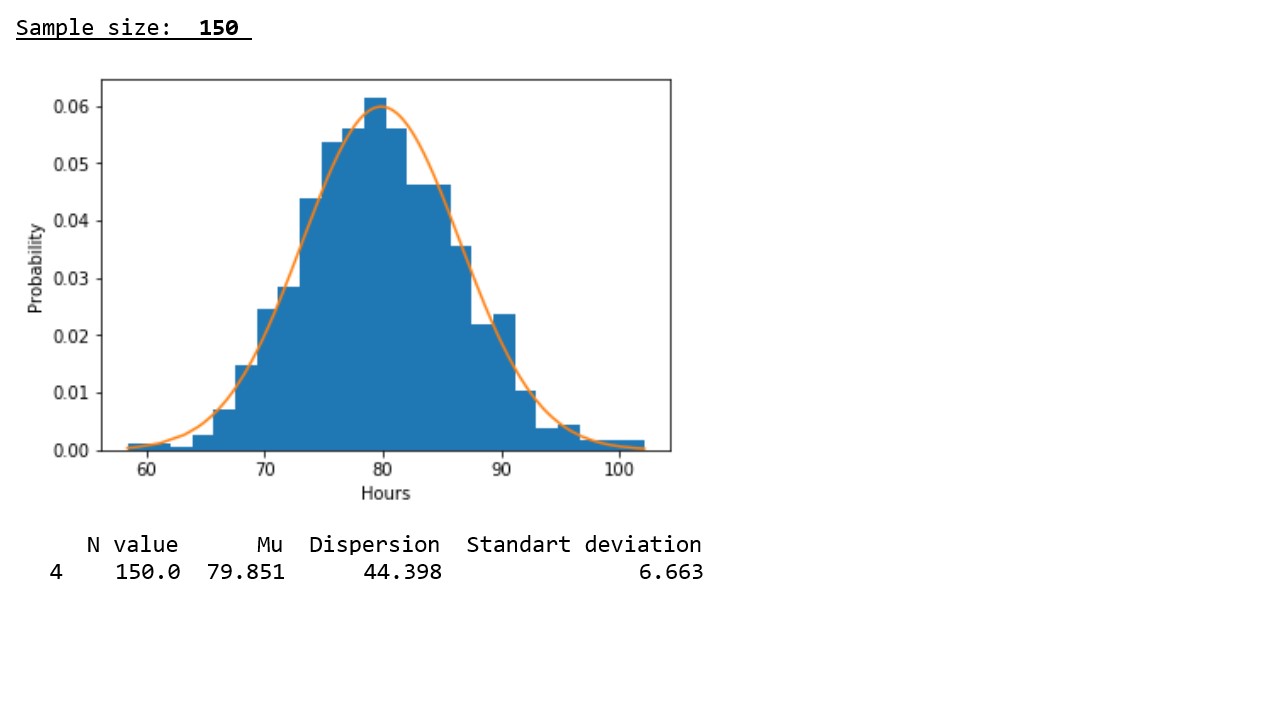
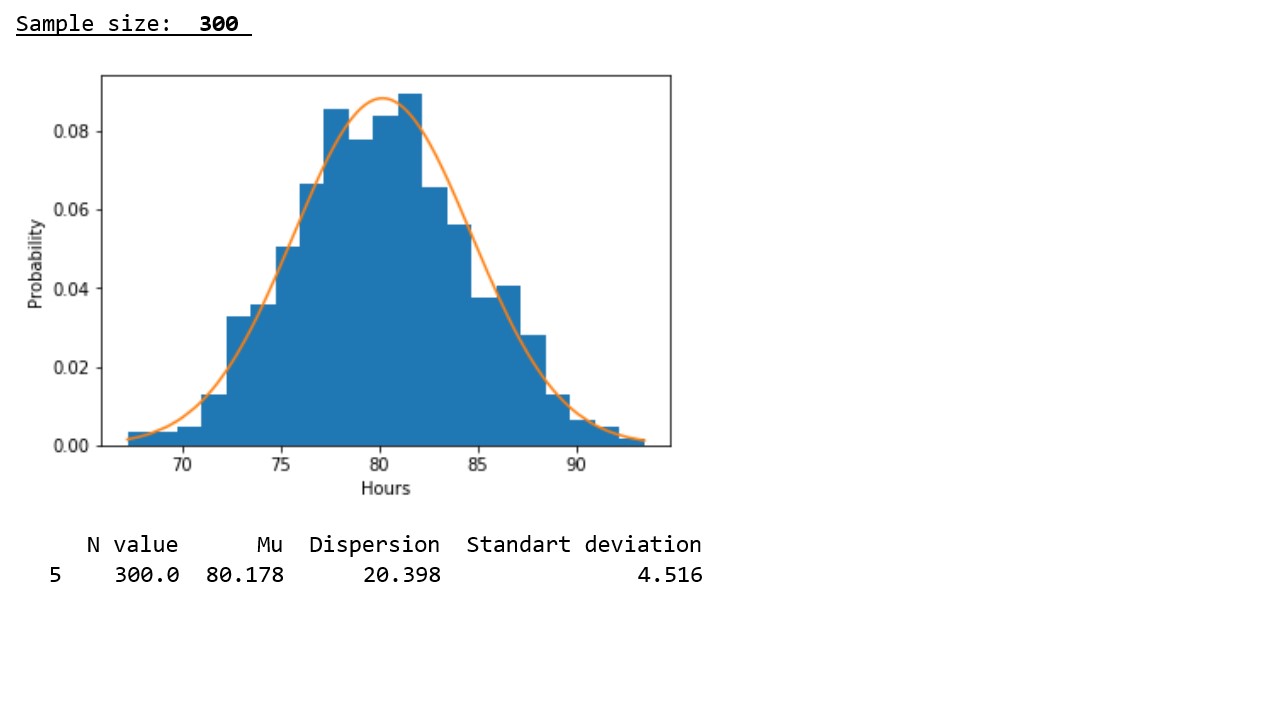
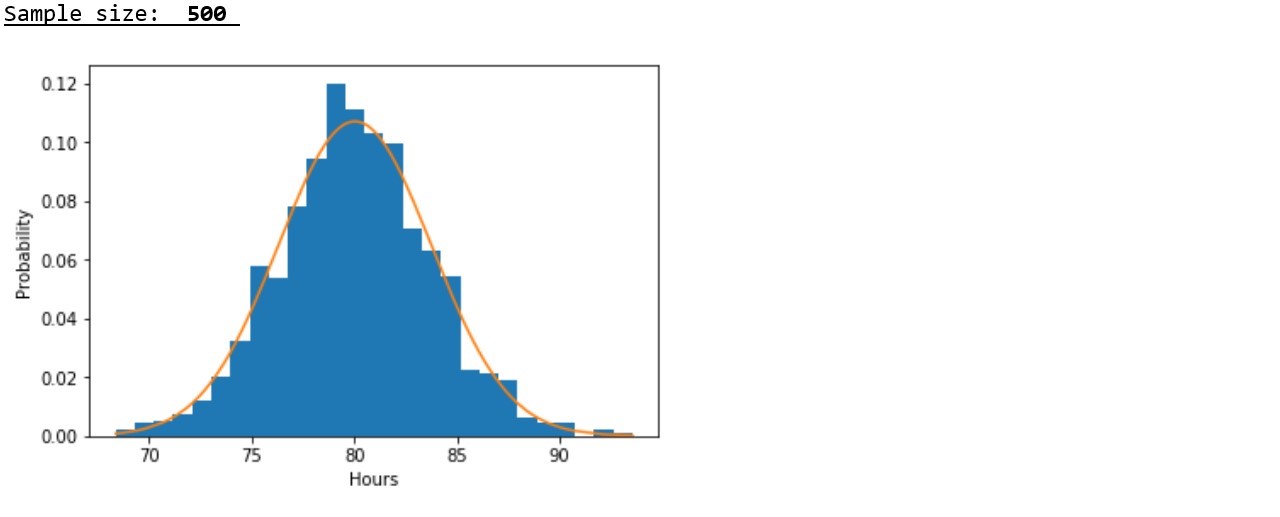
Таблица 2

В соответствии с графическим представлением результатов хорошо прослеживается следующая закономерность: с ростом объема выборки распределение приближается к нормальному и происходит концентрация псевдослучайных величин вокруг выборочного среднего, а выборочное среднее приближается к математическому ожиданию исходного распределения.
В соответствии с данными представленными в таблице, подтверждается закономерность, выявленная на графиках – с ростом объема выборки, значения дисперсий и стандартных отклонений заметно снижаются, что указывает на более плотную концентрацию псевдослучайных величин вокруг выборочных средних.
Но это, еще не все. Мы помним, что в начале статьи было сформировано предложение проверить будут ли с ростом объема выборки уменьшаться отклонения параметров выборки относительно параметров соответствующего нормального распределения.
Как видно (график 3, таблица 3), сколь угодно заметного сокращения отклонений не происходит – параметры выборок прыгают то в плюс, то в минус на разные расстояния и никак не хотят стабильно приближаться к расчетным значениям. Объяснение отсутствия положительной динамики мы обязательно попытаемся найти в следующих исследованиях.
График 3
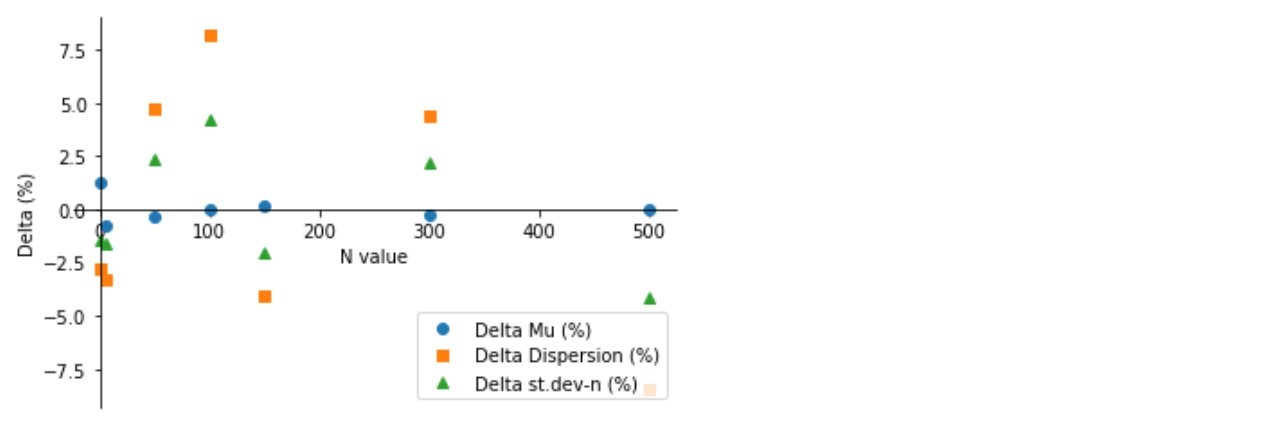
Таблица 3
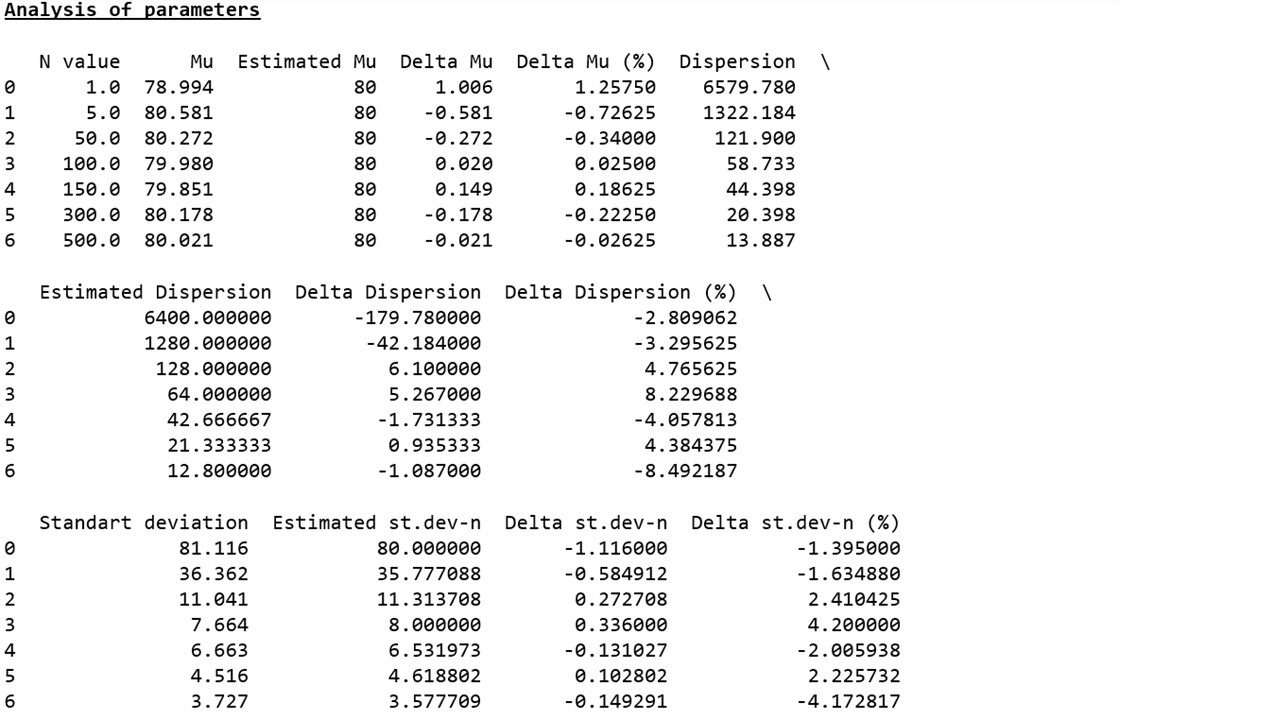
Вместо выводов
Наше исследование, с одной стороны, в очередной раз, подтвердило выводы центральной предельной теоремы о приближении независимых случайно распределенных величин к нормальному распределению с ростом объема выборки, с другой стороны, позволило успешно завершить обучение первого курса большой специализации.
* Развивая логику примера с оборудованием, безотказное время которого составляет 80 часов, по оси «икс» мы обозначим часы – чем меньше времени работает, тем меньше вероятности отказа.
** Здесь требуется иная интерпретация значений по оси «икс» — вероятность того, что прибор отработает в около 80 часов самая высокая и соответственно она уменьшается как при увеличении времени работы (то есть маловероятно, что прибор будет работать намного дольше 80-ти часов), так и при уменьшении времени работы (вероятность того, что прибор выйдет из строя менее чем за 80-ть часов также мала).
Автор: Александр






