Недавно на Хабре вышла статья за авторством MilashchenkoEA Читать полностью »
Рубрика «математическая статистика»
Получаем кривую плотности распределения вероятности… быстрее и точнее
2021-11-04 в 13:12, admin, рубрики: python, Алгоритмы, анализ данных, математика, математическая статистика, плотность вероятностиПолучаем кривую плотности распределения вероятности случайного (или нет) процесса
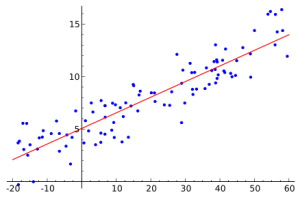
2021-10-24 в 18:07, admin, рубрики: matplotlib, python, Алгоритмы, анализ данных, Анализ и проектирование систем, математика, математическая статистика, моделирование, Программирование, статистический анализВ ходе моей трудовой деятельности неоднократно возникала необходимость построить кривую плотности распределения вероятности по имеющемуся набору числовых данных большого объема различной природы, как случайных, так и не очень. Бывало и такое, что по некоторым причинам, использовать при этом сторонние библиотеки, решающие вопрос, было нежелательно. Приходилось обходится своими силами.
Вероятность выигрыша в покере
2021-09-04 в 6:28, admin, рубрики: математика, математическая статистика, Статистика в IT, теория игрНекоторое время назад обратились ко мне с вопросом, как сделать программу, которая будет выигрывать в покер. После некоторого количества обсуждений, заказчик не захотел узнавать результат моих размышлений на эту тему, посчитал что дорого. Поэтому я разместил эти свои размышления здесь и за бесплатно.
Сразу оговорюсь, что я в покер не играю, и знаю его хуже чем те, кто играет свои первые партии в жизни. Но может это не так уж и важно?
Рассматриваю тот покер, где в колоде 52 карты: 2-10, В, Д, К, Т и 4 масти. Вероятно это Техаский Холдем. На столе в последнем круге пять карт, и по две карты у игроков.
Визуальная теория информации (часть 2)
2020-01-21 в 19:40, admin, рубрики: кодирование, математика, математическая статистика, машинное обучение, сжатие, Статистика в IT, теория вероятностей, теория информации, энтропия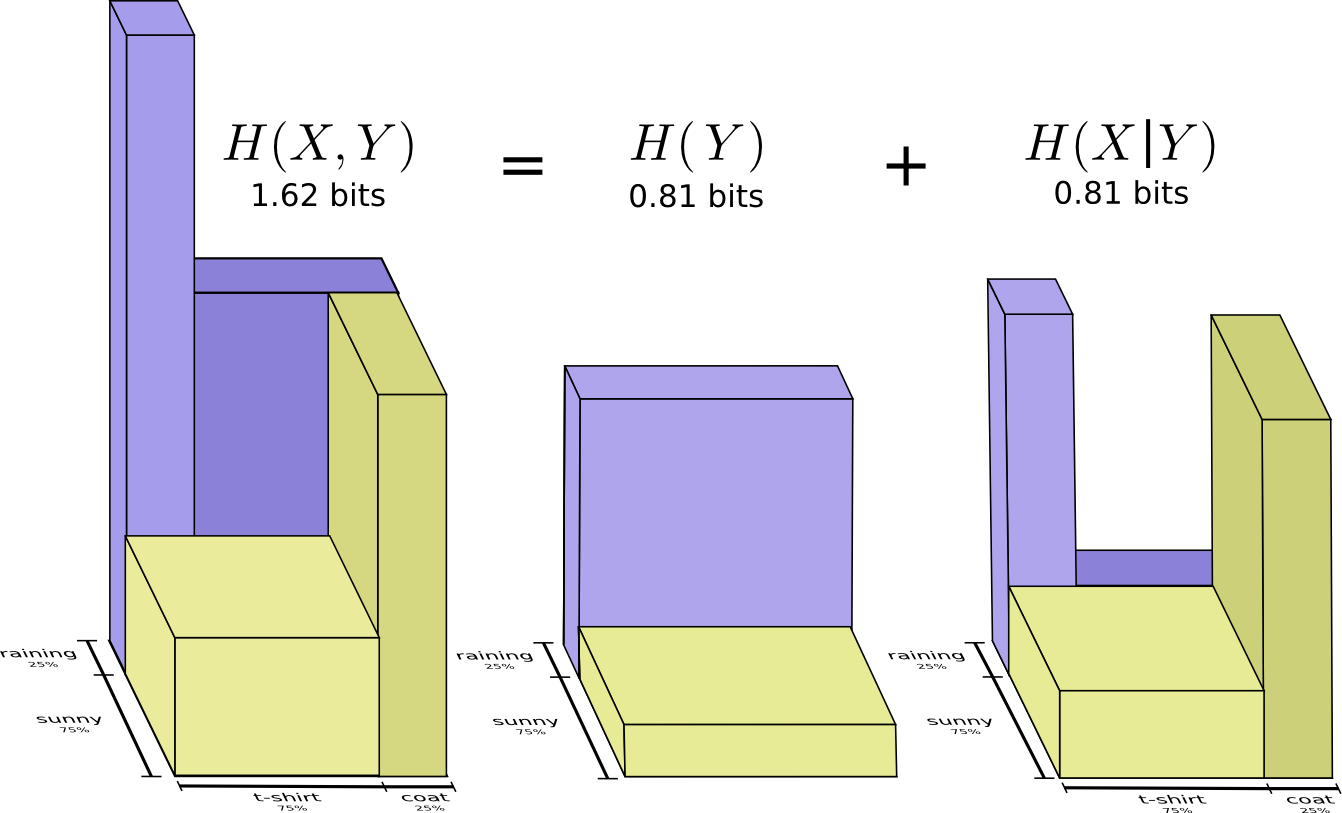
Вторая часть перевода лонгрида посвященного визуализации концепций из теории информации. Во второй части рассматриваются энтропия, перекрестная энтропия, дивергенция Кульбака-Лейблера, взаимная информация и дробные биты. Все концепции снабжены прекрасными визуальными объяснениями.
Для полноты восприятия, перед чтением второй части, рекомендую ознакомиться с первой.
Визуальная теория информации (часть 1)
2020-01-20 в 14:09, admin, рубрики: кодирование, математика, математическая статистика, машинное обучение, сжатие, Статистика в IT, теория вероятностей, теория информации, энтропия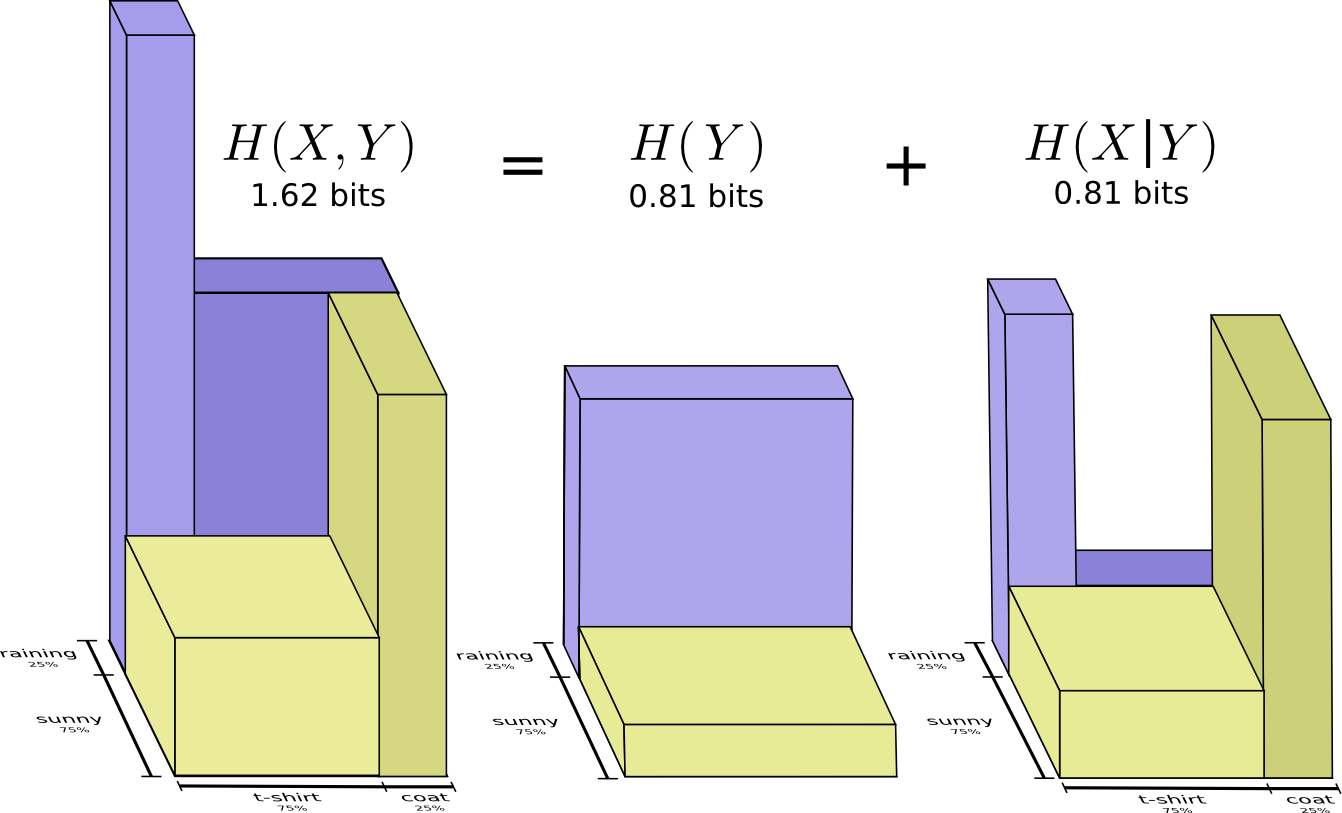
Перевод интересного лонгрида посвященного визуализации концепций из теории информации. В первой части мы посмотрим как отобразить графически вероятностные распределения, их взаимодействие и условные вероятности. Далее разберемся с кодами фиксированной и переменной длины, посмотрим как строится оптимальный код и почему он такой. В качестве дополнения визуально разбирается статистический парадокс Симпсона.
Теория информации дает нам точный язык для описания многих вещей. Сколько во мне неопределенности? Как много знание ответа на вопрос А говорит мне об ответе на вопрос Б? Насколько похож один набор убеждений на другой? У меня были неформальные версии этих идей, когда я был маленьким ребенком, но теория информации кристаллизует их в точные, сильные идеи. Эти идеи имеют огромное разнообразие применений, от сжатия данных до квантовой физики, машинного обучения и обширных областей между ними.
К сожалению, теория информации может казаться пугающей. Я не думаю, что есть какая-то причина для этого. Фактически, многие ключевые идеи могут быть объяснены визуально!
Исследуем утверждение центральной предельной теоремы с помощью экспоненциального распределения
2019-10-11 в 20:52, admin, рубрики: python, математика, математическая статистика, теория вероятностейВместо введения
В статье описывается исследование, проведенное с целью проверки утверждения центральной предельной теоремы о том, что сумма N независимых и одинаково распределенных случайных величин, отобранных практически из любого распределения, имеет распределение, близкое к нормальному. Однако, прежде чем мы перейдем к описанию исследования и более подробному раскрытию смысла центральной предельной теоремы, не лишним будет сообщить, зачем вообще проводилось исследование и кому может быть полезна статья.
В первую очередь, статья может быть полезна всем начинающим постигать основы машинного обучения, в особенности если уважаемый читатель еще и на первом курсе специализации «Машинное обучение и анализ данных». Именно подобного рода исследование требуется провести на заключительной неделе первого курса, указанной выше специализации, чтобы получить заветный сертификат.
Читать полностью »
Теория счастья. Статистика, как научный способ чего-либо не знать
2019-01-12 в 10:36, admin, рубрики: законы подлости, Занимательные задачки, математика, математическая статистика, Научно-популярное, погода, теория вероятности, теория счастьяПродолжаю знакомить читателей Хабра с главами из своей книжки «Теория счастья» с подзаголовком «Математические основы законов подлости». Это ещё не изданная научно-популярная книжка, очень неформально рассказывающая о том, как математика позволяет с новой степенью осознанности взглянуть на мир и жизнь людей. Она для тех кому интересна наука и для тех, кому интересна жизнь. А поскольку жизнь наша сложна и, по большому счёту, непредсказуема, упор в книжке делается, в основном, на теорию вероятностей и математическую статистику. Здесь не доказываются теоремы и не даются основы науки, это ни в коем случае не учебник, а то, что называется recreational science. Но именно такой почти игровой подход позволяет развить интуицию, скрасить яркими примерами лекции для студентов и, наконец, объяснить нематематикам и нашим детям, что же такого интересного мы нашли в своей сухой науке.
Опубликованные главы:
• Введение в мерфологию
• Случайности случайны?
• Головокружительный полёт бутерброда с маслом
• Статистика, как научный способ чего-либо не знать
• Закон арбузной корки и нормальность ненормальности
• Закон зебры и чужой очереди
• Проклятие режиссёра и проклятые принтеры
• Термодинамика классового неравенства
• Случайности случайны?
• Головокружительный полёт бутерброда с маслом
• Статистика, как научный способ чего-либо не знать
• Закон арбузной корки и нормальность ненормальности
• Закон зебры и чужой очереди
• Проклятие режиссёра и проклятые принтеры
• Термодинамика классового неравенства
Речь в этой главе пойдёт о статистике, о погоде и даже о философии. Не пугайтесь, совсем чуть-чуть. Не более того, что можно использовать для tabletalk в приличном обществе.
Правдоподобия, P-значения и кризис воспроизводимости
2018-11-19 в 6:59, admin, рубрики: байесовские методы, математика, математическая статистика, Научно-популярное, статистика, Статистика в ITИли: Как переход от публикации P-значений к публикации функций правдоподобия поможет справиться с кризисом воспроизводимости: личное мнение Элиезера Юдковского.
Комментарий переводчика: Юдковский, автор HPMOR, создатель Lesswrong и прочая и прочая, изложил свою позицию по поводу пользы байесовской статистики в естественных науках в форме диалога. Прямо классический такой диалог из античности или эпохи возрождения, с персонажами, излагающими идеи, обменом колкостями вперемешку с запутанными аргументами и неизбежно тупящим Симплицио. Диалог довольно длинный, минут на двадцать чтения, но по-моему, он того стоит.
Дисклеймеры
- Этот диалог был написан сторонником байесовского подхода. Реплики Учёного в нижеприведённом диалоге могут и не пройти идеологический тест Тьюринга на фреквентизм. Возможно, что они не отдают должное аргументам и контраргументам сторонников частотного подхода к вероятности.
- Автор не рассчитывает, что описанные ниже предложения будут приняты широким научным сообществом в ближайшие десять лет. Тем не менее, это стоило написать.
Если вы ещё не знакомы с правилом Байеса, на сайте Arbital есть подробное введение.
Модератор: Добрый вечер. Сегодня в нашей студии: Учёный, практикующий специалист в области… химической психологии или чего-то типа того; его оппонент Байесовец, который намерен доказать, что кризис воспроизводимости в науке можно как-то преодолеть с помощью замены P-значений на что-то из Байесовской статистики…
Студент: Извините, как это пишется?
Модератор:… и, наконец, ничего не понимающий Студент справа от меня.
Читать полностью »
Модель полиномиальной регрессии
2018-06-15 в 17:03, admin, рубрики: временные ряды, математика, математическая статистика, регрессияВыражаясь простым языком, модель регрессии в математической статистике строится на основе известных данных, в роли которых выступают пары чисел. Количество таких пар заранее определено. Если представить себе, что первое число в паре – это значение координаты 
, а второе – 
, то множество таких пар чисел можно представить на плоскости в декартовой системе координат в виде множества точек. Данные пары чисел берутся не случайно. На практике, как правило, второе число зависит от первого. Построить регрессию – это значит подобрать такую линию (точнее, функцию), которая как можно точнее приближает к себе (аппроксимирует) множество вышесказанных точек.
Рассчитываем вероятности для статьи «Нечестная игра, или как нас обманывают организаторы розыгрышей»
2018-06-05 в 15:13, admin, рубрики: Алгоритмы, Блог компании Cloud4Y, Занимательные задачки, игра, интернет, логические игры, математика, математическая статистика, теория вероятностейСтатья с разбором игры известной торговой сети вызвала у нас в Cloud4Y живой интерес. Вот небольшие отрывки, чтобы ввести вас в курс дела:
Однажды, солнечным весенним утром, почитывая городской форум, я наткнулся на ссылку с простенькой игрой от известной торговой сети. Игра (акция), посвящённая чемпионату мира по футболу, представляла собой незамысловатое поле три на три, заполненное футбольными мячами. Кликая по мячу, мы открывали картинку с тем или иным товаром. При открытии трёх одинаковых картинок участнику гарантировалось бесплатное получение данного товара в одном из магазинов сети. Также под одним из мячей имелось изображение красной карточки, открытие которой означало конец игры.
Автор статьи принялся расследовать причины своего проигрыша и по результатам расчетов выяснил следующее:
Быстрый набросок формул на салфетке, и выяснилось, что вероятность выигрыша — 1/4. Для 5 полей пришлось повозиться, но расчётная вероятность получилась также 25%.
...
Запустив скрипт, я получил неожиданный результат — 25% выигрышей. Поиграв с количеством выигрышных элементов и общим количеством полей, я выяснил, что вероятность выигрыша в подобной игре не зависит от количества полей и равна единице, поделенной на количество выигрышных элементов, увеличенных на единицу.
Нас заинтересовала правильность такого расчета и, заменив салфетку на Excel, мы взялись за дело в поисках математической истины. Читателей, увлекающихся теорией вероятности, приглашаем под кат, дабы проверить правильность наших вычислений.
Читать полностью »