Методы Монте-Карло для марковских цепей (MCMC). Введение

Привет!

Напоминаем, что ранее мы анонсировали книгу "Машинное обучение без лишних слов" — и теперь она уже в продаже. Притом, что для начинающих специалистов по МО книга действительно может стать настольной, некоторые темы в ней все-таки затронуты не были. Поэтому всем заинтересованным предлагаем перевод статьи Саймона Керстенса о сути алгоритмов MCMC с реализацией такого алгоритма на Python.

Методы Монте-Карло для марковских цепей (MCMC) – это мощный класс методов для выборки из вероятностных распределений, известных лишь вплоть до некоторой (неизвестной) нормировочной константы.
Однако прежде, чем углубиться в MCMC, давайте обсудим, зачем вам вообще может понадобиться делать такую выборку. Ответ таков: вам могут быть интересны либо сами образцы из выборки (например, для определения неизвестных параметров методом байесовского вывода), либо для аппроксимации ожидаемых значений функций относительно вероятностного распределения (например, для расчета термодинамических величин по распределению состояний в статистической физике). Иногда нас интересует только мода распределения вероятностей. В данном случае получаем ее методом числовой оптимизации, поэтому делать полную выборку не обязательно.

Оказывается, что выборка из любых вероятностных распределений кроме самых примитивных – сложная задача. Метод обратного преобразования – элементарный прием для выборки из вероятностных распределений, который, однако, требует использовать кумулятивную функцию распределения, а для ее использования, в свою очередь, нужно знать нормировочную константу, которая обычно неизвестна. В принципе, нормировочную константу можно получить методом численного интегрирования, но такой способ быстро становится неосуществимым при увеличении количества размерностей. Выборка с отклонением не требует нормализованного распределения, но, чтобы эффективно ее реализовать, требуется очень много знать об интересующем нас распределении. Вдобавок, этот метод серьезно страдает от проклятия размерностей – это означает, что его эффективность стремительно падает с увеличением количества переменных. Именно поэтому нужно толково организовать получение репрезентативных выборок из вашего распределения – не требующих знать нормировочную константу.

Алгоритмы MCMC – это класс методов, предназначенных именно для этого. Они восходят к эпохальной статье Метрополиса и др.; Метрополис разработал первый MCMC-алгоритм, названный в его честь и предназначенный для вычисления равновесного состояния двумерной системы жестких сфер. Фактически, исследователи искали универсальный метод, который позволил бы вычислять ожидаемые значения, встречающиеся в статистической физике.
В этой статье будут рассмотрены основы выборки по MCMC.

МАРКОВСКИЕ ЦЕПИ

Теперь, когда мы понимаем, зачем нам делать выборку, перейдем к сердцу MCMC: марковским цепям. Что такое марковская цепь? Не вдаваясь в технические детали, можно сказать, что марковская цепь – это случайная последовательность состояний в некотором пространстве состояний, где вероятность выбора определенного состояния зависит только от текущего состояния цепи, но не от ее прежней истории: эта цепь лишена памяти. В определенных условиях марковская цепь имеет уникальное стационарное распределение состояний, к которому сходится, преодолев определенное количество состояний. После такого числа состояний состояния в марковской цепи получают инвариантное распределение.

Для выборки из распределения 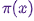алгоритм MCMC создает и имитирует марковскую цепь, чье стационарное распределение равно 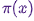; это означает, что после начального «затравочного» периода, состояния такой марковской цепи распределяются по принципу 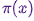. Следовательно, нам придется всего лишь сохранить состояния, чтобы получить образцы из .

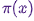В образовательных целях давайте рассмотрим как дискретное пространство состояний, так и дискретное «время». Ключевая величина, характеризующая марковскую цепь – это оператор перехода 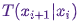, указывающий вероятность нахождения в состоянии 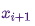в момент времени 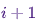, при условии, что цепь находится в состоянии 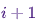во время i.
Теперь просто для интереса (и в качестве демонстрации) давайте по-быстрому сплетем марковскую цепь, имеющую уникальное стационарное распределение. Начнем с некоторых импортов и настроек для графиков:

%matplotlib notebook
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = [10, 6]
np.random.seed(42)

Марковская цепь будет обходить дискретное пространство состояний, образуемое тремя состояниями погоды:

state_space = ("sunny", "cloudy", "rainy")

В дискретном пространстве состояний оператор перехода – это просто матрица. В нашем случае столбцы и строки соответствуют солнечной, облачной и дождливой погоде. Выберем относительно разумные значения для вероятностей всех переходов:

transition_matrix = np.array(((0.6, 0.3, 0.1),
                              (0.3, 0.4, 0.3),
                              (0.2, 0.3, 0.5)))

В строках указаны состояния, в которых в настоящее время может находиться цепь, а в столбцах – состояния, в которые цепи могут перейти. Если взять «временной» шаг марковской цепи за один час, то, при условии, что сейчас солнечно, существует 60% вероятность, что солнечная погода сохранится в течение ближайшего часа. Также есть 30% вероятность, что в следующий час будет облачная погода, и 10%-я вероятность, что сразу же после солнечной погоды пойдет дождь. Это также означает, что значения в каждом ряду в сумме дают единицу.
Давайте немного погоняем нашу марковскую цепь:

n_steps = 20000
states = [0]
for i in range(n_steps):
    states.append(np.random.choice((0, 1, 2), p=transition_matrix[states[-1]]))
states = np.array(states)

Можем наблюдать, как марковская цепь сходится к стационарному распределению, рассчитывая эмпирическую вероятность каждого из состояний как функцию длины цепи:

def despine(ax, spines=('top', 'left', 'right')):
    for spine in spines:
        ax.spines[spine].set_visible(False)

fig, ax = plt.subplots()
width = 1000
offsets = range(1, n_steps, 5)
for i, label in enumerate(state_space):
    ax.plot(offsets, [np.sum(states[:offset] == i) / offset 
            for offset in offsets], label=label)
ax.set_xlabel("number of steps")
ax.set_ylabel("likelihood")
ax.legend(frameon=False)
despine(ax, ('top', 'right'))
plt.show()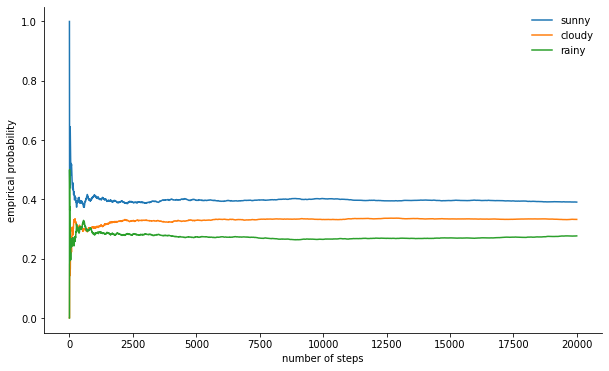

РОДОНАЧАЛЬНИК ВСЕХ MCMC: АЛГОРИТМ МЕТРОПОЛИСА-ГАСТИНГСА

Конечно, все это очень интересно, но вернемся к процессу выборки произвольного вероятностного распределения . Оно может быть либо дискретным, и в этом случае мы и далее будем говорить о матрице перехода 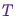, либо непрерывным, и в этом случае 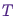будет переходным ядром. Здесь и далее речь пойдет о непрерывных распределениях, но все концепции, которые мы здесь рассмотрим, применимы и к дискретным случаям.

Если бы мы смогли спроектировать переходное ядро таким образом, чтобы следующее состояние уже было выведено из , то этим можно было бы и ограничиться, так как наша марковская цепь… непосредственно делала бы выборку из . К сожалению, чтобы добиться этого, нам нужна возможность делать выборку из , чего мы делать не можем – иначе вы бы этого не читали, верно?

Обходной путь – разбить переходное ядро 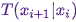на две части: шаг проб (proposal step) и шаг приема/отбрасывания (acceptance/rejection step). На шаге проб фигурирует вспомогательное распределение 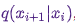, из которого выбираются возможные следующие состояния цепочки. Мы не только можем делать выборку из этого распределения, но и в силах произвольно выбирать само распределение. Однако, при проектировании следует стремиться прийти к такой конфигурации, в которой образцы, взятые из этого распределения, минимально коррелировали бы с актуальным состоянием и одновременно имели хорошие шансы пройти этап приема. Вышеуказанный этап приема/отбрасывания – вторая часть переходного ядра; на данном этапе корректируются ошибки, содержавшиеся в пробных состояниях, выбранных из 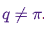. Здесь вычисляется вероятность успешного приема 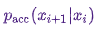и принимается проба 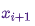с такой вероятностью в качестве следующего состояния в цепи. Получение следующего состояния 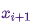из 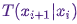тогда выполняется следующим образом: сначала пробное состояние 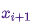берется из 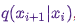. Затем оно принимается в качестве следующего состояния с вероятностью или отбрасывается с вероятностью 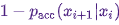, и в последнем случае актуальное состояние копируется и используется в качестве следующего.
Следовательно, имеем

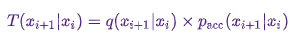
Достаточным условием для того, чтобы марковская цепь имела в качестве стационарного распределения является следующее: переходное ядро должно подчиняться детальному равновесию или, как пишут в физической литературе, микроскопической обратимости:

.

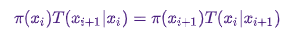Это означает, что вероятность находиться в состоянии 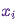и перейти оттуда в 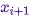должна быть равна вероятности обратного процесса, то есть, быть в состоянии 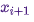и перейти в состояние 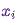. Ядра перехода большинства MCMC-алгоритмов удовлетворяют этому условию.
Для того, чтобы двухчастное ядро перехода подчинялось детальному равновесию, нужно правильно выбрать , то есть, добиться, чтобы оно позволяло корректировать любые асимметрии в потоке вероятностей от / до 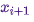или 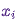. Алгоритм Метрополиса-Гастингса использует критерий приемлемости Метрополиса:

.

А вот здесь начинается магия: известно нам только до константы, но это не имеет значения, поскольку данная неизвестная константа обнуляет выражение для ! Именно это свойство paccpacc обеспечивает работу алгоритмов, основанных на алгоритме Метрополиса-Гастингса, на ненормированных распределениях. Часто используются симметричные вспомогательные распределения с 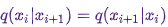, и в таком случае алгоритм Метрополиса-Гастингса редуцируется до оригинального (менее общего) алгоритма Метрополиса, разработанного в 1953 году. В оригинальном алгоритме

.

В таком случае полное переходное ядро Метрополиса-Гастингса можно записать как

.

РЕАЛИЗУЕМ АЛГОРИТМ МЕТРОПОЛИСА-ГАСТИНГСА НА PYTHON

Отлично, теперь, когда мы разобрались в принципе работы алгоритма Метрополиса-Гастингса, давайте перейдем к его реализации. Сначала установим логарифмическую вероятность того распределения, из которого собираемся делать выборку – без нормировочных констант; предполагается, что мы их не знаем. Далее работаем со стандартным нормальным распределением:

def log_prob(x):
     return -0.5 * np.sum(x ** 2)

Далее выбираем симметричное вспомогательное распределение. В целом, производительность алгоритма Метрополиса-Гастингса можно повысить, если включить во вспомогательное распределение уже известную вам информацию о том распределении, из которого вы хотите сделать выборку. Упрощенный подход выглядит так: берем текущее состояние x и выбираем пробу из , то есть, задаем некоторую величину шага Δ и переходим влево или вправо от нашего текущего состояния не более чем на :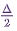

def proposal(x, stepsize):
    return np.random.uniform(low=x - 0.5 * stepsize, 
                             high=x + 0.5 * stepsize, 
                             size=x.shape)

Наконец, вычисляем вероятность того, что предложение будет принято:

def p_acc_MH(x_new, x_old, log_prob):
    return min(1, np.exp(log_prob(x_new) - log_prob(x_old)))

Теперь собираем все это вместе в по-настоящему краткую реализацию этапа построения выборки для алгоритма Метрополиса-Гастингса:

def sample_MH(x_old, log_prob, stepsize):
    x_new = proposal(x_old, stepsize)
    # здесь мы определяем, принимается новое состояние или нет:
    # мы равномерно выбираем случайное число из [0,1] и сравниваем
    # его с вероятностью успешного приема
    accept = np.random.random() < p_acc(x_new, x_old, log_prob)
    if accept:
        return accept, x_new
    else:
        return accept, x_old

Кроме следующего состояния в марковской цепи, x_new или x_old, мы также возвращаем информацию о том, был ли принят шаг MCMC. Это позволит нам отслеживать динамику приема проб. В заключение данной реализации напишем функцию, которая будет итеративно вызывать sample_MH и таким образом строить марковскую цепь:

def build_MH_chain(init, stepsize, n_total, log_prob):

    n_accepted = 0
    chain = [init]

    for _ in range(n_total):
        accept, state = sample_MH(chain[-1], log_prob, stepsize)
        chain.append(state)
        n_accepted += accept
    
    acceptance_rate = n_accepted / float(n_total)
    
    return chain, acceptance_rate

ТЕСТИРУЕМ НАШ АЛГОРИТМ МЕТРОПОЛИСА-ГАСТИНГСА И ИССЛЕДУЕМ ЕГО ПОВЕДЕНИЕ

Наверное, теперь вам не терпится увидеть все это в действии. Этим и займемся, примем несколько информированных решений об аргументах stepsize и n_total:

chain, acceptance_rate = build_MH_chain(np.array([2.0]), 3.0, 10000, log_prob)
chain = [state for state, in chain]
print("Acceptance rate: {:.3f}".format(acceptance_rate))
last_states = ", ".join("{:.5f}".format(state) 
                        for state in chain[-10:])
print("Last ten states of chain: " + last_states)
Acceptance rate: 0.722
Last ten states of chain: -0.84962, -0.84962, -0.84962, -0.08692, 0.92728, -0.46215, 0.08655, -0.33841, -0.33841, -0.33841

Все хорошо. Итак, это сработало? Мы добились принятия проб примерно в 71% случаев, и у нас есть цепочка состояний. Следует отбросить несколько первых состояний, в которых цепь еще не сошлась к своему стационарному распределению. Давайте проверим, на самом ли деле у выбранных нами состояний – нормальное распределение:

def plot_samples(chain, log_prob, ax, orientation='vertical', normalize=True,
                 xlims=(-5, 5), legend=True):
    from scipy.integrate import quad
    
    ax.hist(chain, bins=50, density=True, label="MCMC samples",
           orientation=orientation)
    # вычисляем нормировочную константу нашего PDF
    if normalize:
        Z, _ = quad(lambda x: np.exp(log_prob(x)), -np.inf, np.inf)
    else:
        Z = 1.0
    xses = np.linspace(xlims[0], xlims[1], 1000)
    yses = [np.exp(log_prob(x)) / Z for x in xses]
    if orientation == 'horizontal':
        (yses, xses) = (xses, yses)
    ax.plot(xses, yses, label="true distribution")
    if legend:
        ax.legend(frameon=False)
    
fig, ax = plt.subplots()
plot_samples(chain[500:], log_prob, ax)
despine(ax)
ax.set_yticks(())
plt.show()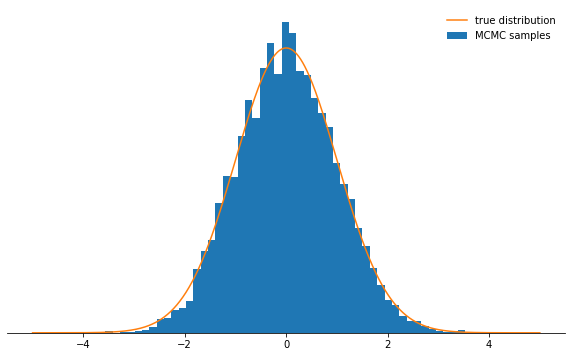

Выглядит отлично!

Что же с параметрами stepsize и n_total? Обсудим сначала размер шага: он определяет, насколько может быть удалено пробное состояние от текущего состояния цепи. Следовательно, это параметр вспомогательного распределения q, контролирующий, насколько велики будут случайные шаги, совершаемые цепью Маркова. Если размер шага слишком велик, то пробные состояния часто оказываются в хвосте распределения, где значения вероятности низкие. Механизм выборки Метрополиса-Гастингса отбрасывает большинство из этих шагов, вследствие чего темпы приема снижаются, и сходимость значительно замедляется. Убедитесь сами:

def sample_and_display(init_state, stepsize, n_total, n_burnin, log_prob):
    chain, acceptance_rate = build_MH_chain(init_state, stepsize, n_total, log_prob)
    print("Acceptance rate: {:.3f}".format(acceptance_rate))
    fig, ax = plt.subplots()
    plot_samples([state for state, in chain[n_burnin:]], log_prob, ax)
    despine(ax)
    ax.set_yticks(())
    plt.show()
    
sample_and_display(np.array([2.0]), 30, 10000, 500, log_prob)
Acceptance rate: 0.116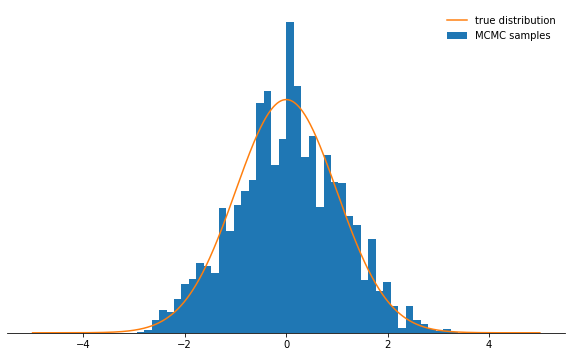

Не очень круто, правда? Теперь кажется, что лучше всего задать крошечный размер шага. Оказывается, что и это не слишком умное решение, поскольку марковская цепь станет исследовать вероятностное распределение очень медленно, и поэтому также не станет сходиться настолько быстро, как с хорошо подобранным размером шага:

sample_and_display(np.array([2.0]), 0.1, 10000, 500, log_prob)
Acceptance rate: 0.992

Независимо от того, как вы выберете параметр размера шага, марковская цепь в конце концов сойдется к стационарному распределению. Но на это может потребоваться мноооого времени. Время, в течение которого мы будем симулировать марковскую цепь, задается параметром n_total — он просто определяет, сколько состояний марковской цепи (и, следовательно, выбранных образцов) у нас в итоге будет. Если цепь сходится медленно, то требуется увеличить n_total, чтобы марковская цепь успела «забыть» исходное состояние. Поэтому оставим размер шага крошечным и увеличим количество образцов, нарастив параметр n_total:

sample_and_display(np.array([2.0]), 0.1, 500000, 25000, log_prob)
Acceptance rate: 0.990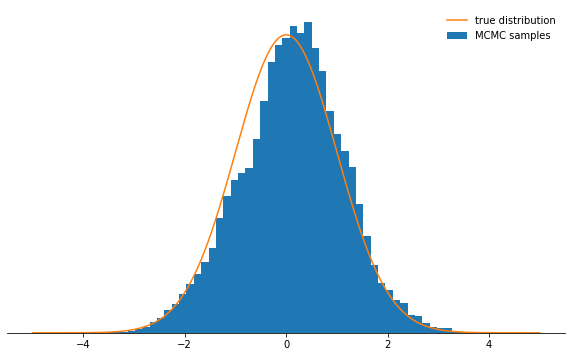

Мееееедленно идем к цели…

ВЫВОДЫ

Учитывая все вышеизложенное, надеюсь, теперь вы интуитивно уловили суть алгоритма Метрополиса-Гастингса, его параметров, и понимаете, почему это исключительно полезный инструмент для выборки из нестандартных вероятностных распределений, которые могут встретиться вам на практике.

Настоятельно рекомендую вам самим поэкспериментировать с кодом, приведенным здесь – так вы освоитесь с поведением алгоритма в различных обстоятельствах и глубже его поймете. Попробуйте несимметричное вспомогательное распределение! Что будет, если не настроить критерий приема как следует? Что произойдет, если попытаться сделать выборку из бимодального распределения? Можете ли придумать способ автоматической настройки размера шага? Какие здесь есть подводные камни? Ответьте на эти вопросы самостоятельно!

Автор: ph_piter

Источник