Начнем наш сегодняшний путь с задачи
Три айтишника — Маша, Вася и Петя — пошли в поход. После ужина они решают, кто будет мыть посуду. Петя дежурит один, а Маша с Васей — вдвоём. Значит, нужно выбрать Петю с вероятностью
, а Машу с Васей — с вероятностью
Под рукой — только честная монетка. Как с её помощью устроить такой жребий?

Когда мы обсуждали эту задачу со студентами, они предложили способ, который мы назовем базовым алгоритмом. Бросим монету дважды:
Если выпали два орла — дежурит Петя; если один орёл и одна решка — Маша с Васей; если две решки — перебрасываем
В итоге жребий будет честным: Петя будет дежурить ровно в трети игр
Сколько бросков потребуется, чтобы выбрать дежурного? Иногда достаточно двух, но бывает, что и десять — если очень не везёт
В среднем на это уходит броска. Попробуйте посчитать сами — а чуть позже мы сделаем это вместе
Возникает вопрос: можно ли выбрать дежурного побыстрее?
Существует ли алгоритм, для которого ожидаемое число бросков меньше, чем для базового?
Оказывается, ответ да: существует простой, но неочевидный метод, позволяющий смоделировать событие с вероятностью — и в среднем требует не больше двух бросков. Он называется алгоритмом Кнута–Яо
Версия этого текста со всеми формальными определениями и техническими деталями будет выложена в моем телеграм канале Кроссворд Тьюринга
Подписывайтесь!)
В этой статье мы пройдём весь путь к этому алгоритму. Начнём с базового алгоритма, научимся оценивать, сколько бросков он требует в среднем, и найдём границу, быстрее которой работать невозможно. А затем построим тот алгоритм, который этой границы достигает — оптимальный для вероятности
После этого мы обобщим идею: научимся моделировать любую вероятность, а в финале — и любое дискретное распределение. Появится важное понятие, называемое энтропией, которое описывает, сколько бросков нужно для генерации распределения
А в самом конце — как всегда, красивая задача
Но прежде всего — разберёмся, откуда в базовом алгоритме появляется

Задача. Игрок бросает пару монет, пока на одной из них не выпадет орёл. Сколько в среднем продлится эта игра?
Будем считать, что ход — это бросок пары монет. Обозначим за ожидаемое количество ходов в игре. Посмотрим, из чего оно складывается:
-
Первый ход совершается всегда — его вклад в
равен
-
Второй происходит только тогда, когда на обеих монетах выпали решки. Это случается в
игр, то есть его вклад в
равен
-
Каждый последующий ход происходит в
раза реже и даёт вклад в
раза меньше, чем предыдущий.
Тогда:
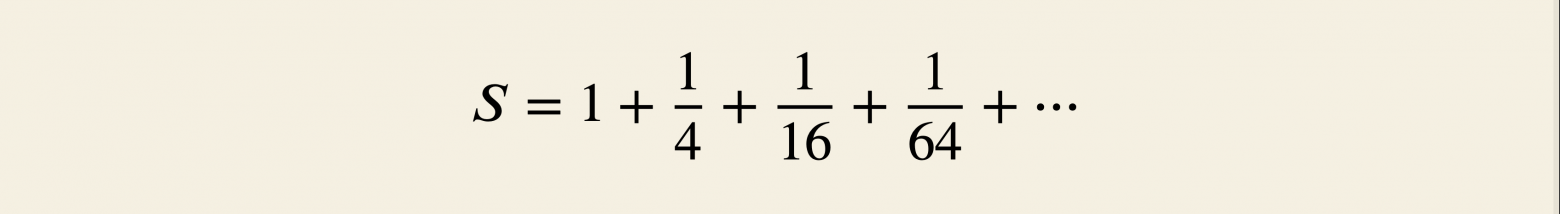
Как считать сумму геометрической прогрессии
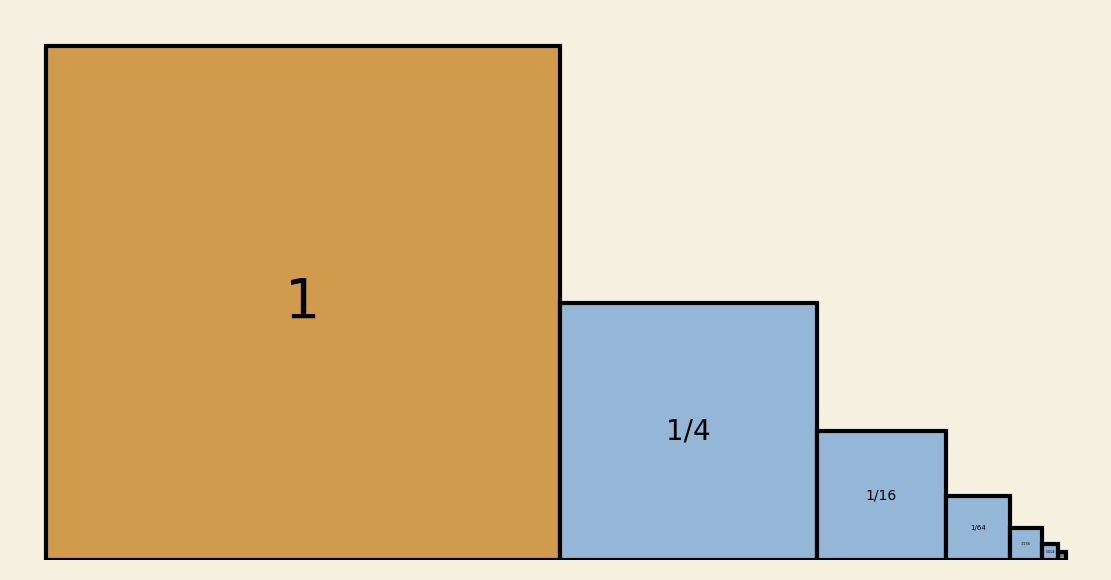
Число — площадь гусеницы (фигуры на картинке). Она состоит из жёлтого квадрата и хвоста. Но хвост — та же гусеница, уменьшенная вдвое по обеим координатам и в

Тоже самое можно получить и с помощью теории вероятностей: первый шаг происходит всегда, а дальше — с вероятностью игра начинается заново
Таким образом:
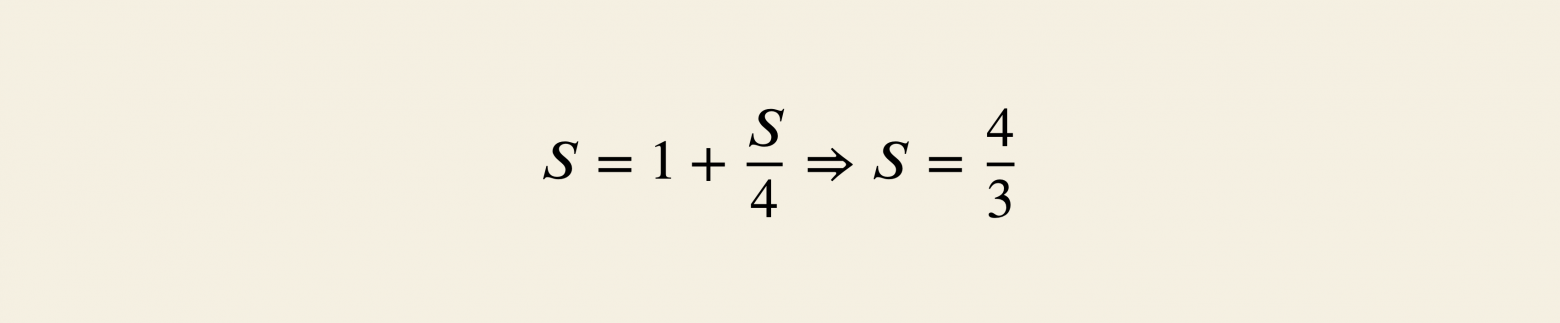


Ход состоит из двух бросков, а значит их ожидаемое число это
Можно придумать и другие похожие способы выбрать дежурного
Например, бросать три монеты за шаг: из восьми возможных троек два варианта отдать Пете, четыре — Маше и Васе, а оставшиеся два — перебрасывать. Можно использовать четыре монеты, выбрать 5 вариантов для Пети, 10 — для Маши и Васи
Упражнение. Найдите ожидаемое время работы этих двух алгоритмов
Такие схемы устроены одинаково: на каждом шаге бросается одно и то же число монет, и в зависимости от выпавшего набора принимается решение или перебрасываем
Назовём такие алгоритмы пошаговыми
Нет смысла бросать одну монету за раз. Если бросать дважды — возможен только базовый алгоритм. Остальные схемы требуют не меньше трёх бросков уже на первом шаге, а значит работают медленнее, чем 8/3. Получается, базовый алгоритм — самый быстрый среди пошаговых
Может быть, базовый алгоритм оптимален? Чтобы ответить, нужно не просто сравнивать схемы между собой, а оценить снизу ожидаемое число бросков. То есть найти границу, быстрее которой не может работать никакой алгоритм, даже самый изощрённый. Сейчас мы это сделаем

Представим, что кто-то придумал хитрый алгоритм, совсем не похожий на базовый. Он может действовать как угодно — принимать решение по длине серий, по чётности, по позициям орлов. Верно одно: он выбирает Петю с вероятностью , а Машу с Васей — с вероятностью
. Мы не знаем, как он устроен, но хотим оценить ожидаемое число бросков
Обозначим за вероятность того, что, действуя по алгоритму, нам придётся бросить монетку хотя бы
раз. Тогда, как и в прошлом разделе:
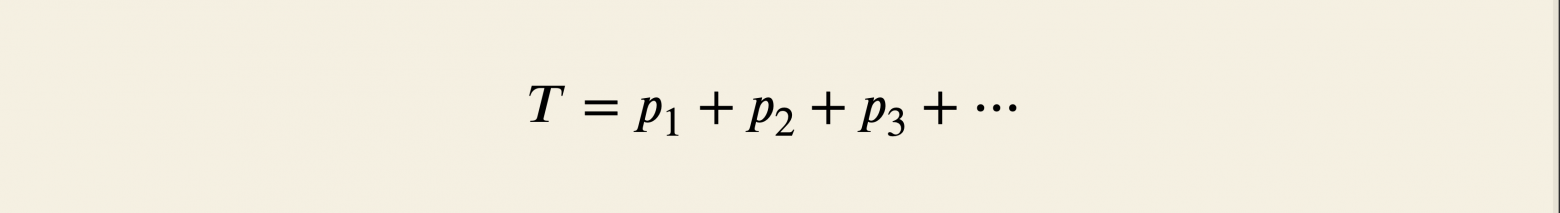
Докажем, что вероятность не может быть слишком малой
Утверждение. Для любого
выполняется неравенство
Доказательство оценки
-
Заметим, что после
броска возможны
различных исходов. Оценим, для скольких из них алгоритм точно продолжает работу
-
Если бы алгоритм гарантированно завершался после
броска, исходы делились бы в отношении
— но
не делится на три
-
Значит, для какого-то исхода алгоритм продолжит работу, следовательно, с вероятностью не меньше
придётся бросить
раз
Получается, ожидаемое число бросков можно оценить так:

Эту сумму можно найти, используя уже знакомое вычисление :
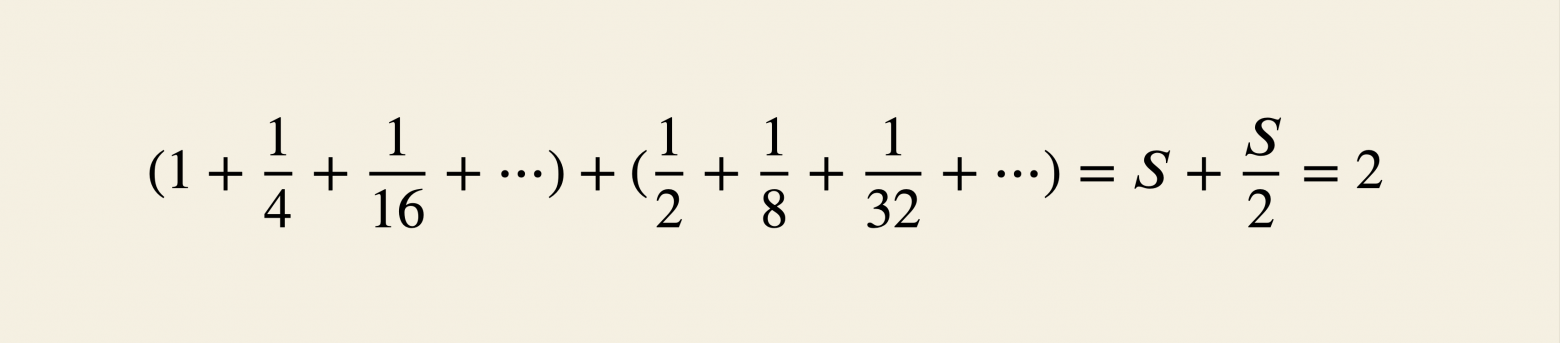
Упражнение. Пусть для некоторого алгоритма
. Сколько есть исходов для
бросков, после которых он остановится?
Возникает естественный вопрос:
Можно ли достичь этой границы?
Существует ли алгоритм, для которого среднее число бросков равно ?
В следующем разделе мы разберёмся, как этого добиться

Мы хотим построить алгоритм, в котором ожидаемое число бросков равно . Мы знаем, что это возможно только если после любого числа бросков один результат ведёт к продолжению, а остальные — к завершению
Запишем этот единственный результат как слово из букв (решка) и
(орёл). Например,
значит, что после решки, орла и двух решек алгоритм всё ещё работает
Назовём эти слова незавершёнными
Незавершённые слова продолжают друг друга. Если — незавершённое, то и
тоже. То есть каждое следующее незавершённое слово получается из предыдущего приписыванием буквы в конец
Например, алгоритм может продолжаться на таких словах:

Все они — начальные отрезки одной бесконечной последовательности
Назовём её управляющей последовательностью алгоритма

Алгоритм продолжает работу после n бросков тогда и только тогда, когда результат этих бросков совпадает с первыми n буквами управляющей последовательности
Теперь легко описать алгоритмы с ожидаемым числом бросков
Утверждение. Алгоритм в среднем требует
броска, если он работает до тех пор, пока результат совпадает с некой последовательностью — и завершает работу при первом отклонении
Можно выбрать любую управляющую последовательность (они ничем не отличаются друг от друга). Алгоритм особенно прост, если она состоит из одних решек: бросаем монетку до первого орла и принимаем решение
Упражнение. Покажите, что ожидаемое число бросков до первого орла равно
, не используя бесконечную сумму
Именно на основе такой управляющей последовательности — из одних решек — мы сейчас построим алгоритм, решающий исходную задачу

Перед нами почти готовый алгоритм. Мы уже поняли, в какие моменты он останавливается. Осталось определить для них результат жребия так, чтобы вероятность равнялась
Алгоритм завершается, если на -м броске впервые выпал орёл, а до этого были только решки. Вероятность такого исхода равна
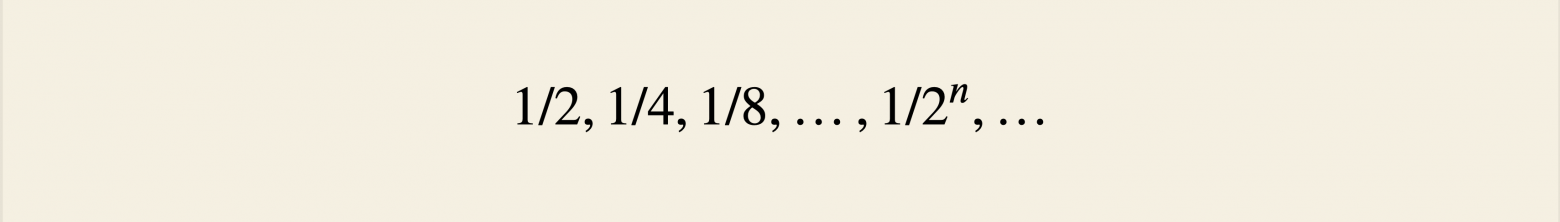
После завершения алгоритма мы с определенностью понимаем, кто идет дежурить. Таким образом все исходы делятся на две группы, и вероятность дежурства Пети складывается из вероятностей исходов первой группы, а Маши с Васей — из вероятностей исходов второй
Получается, мы должны распределить числа на две суммы так, чтобы первая равнялась
, а вторая —
Каждое из чисел в ряду в два раза меньше предыдущего, поэтому сумма чисел на чётных местах () в два раза меньше суммы чисел на нечётных (
). Получается, что они составляют
и
всей суммы соответственно
Упражнение. Докажите, что это единственный способ разделить слагаемые так, чтобы суммы были равны
и
Таким образом, получаем простой и естественный алгоритм
Алгоритм. Бросаем монетку до первого орла. Если он выпал на чётном броске — дежурит Петя, иначе — Маша и Вася
Так мы завершили путь к оптимальному алгоритму: начали с наивного решения, вывели формулу для среднего числа бросков, нашли границу, быстрее которой никакой алгоритм работать не может — и построили алгоритм, который эту границу достигает
Алгоритм, который мы построили, точно реализует вероятность — и делает это с минимально возможным числом бросков. Теперь хочется понять:
Можно ли тем же способом смоделировать любую вероятность?

Мы построили алгоритм, который отправляет Петю дежурить с вероятностью , и делает это в среднем за два броска. Оказывается, то же самое можно сделать для любой вероятности
от
до
Как и раньше, будем бросать монетку до первого орла. Алгоритм завершается, если на -м броске впервые выпал орёл, а до этого были только решки. Этот исход даёт вклад
в вероятность, и мы хотим выбрать такие исходы, чтобы сумма вероятностей была равна
. Как это сделать
Напомним, что такое двоичная запись числа. Последовательности нулей и единиц можно сопоставить числу от
до
. Например:
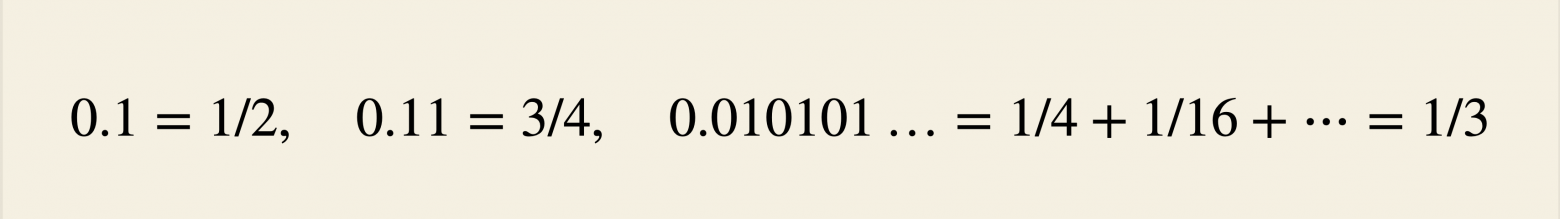
В таком случае называют двоичной записью числа
Утверждение. У любого числа
от 0 до 1 есть двоичная запись (возможно, бесконечная)
Почему двоичная запись всегда существует
Построим последовательность нулей и единиц пошагово:
-
Разобьём отрезок
пополам. Если
лежит в левой половине, пишем
, если в правой (или посередине) —
-
Выберем ту половину, в которой оказалась точка, и теперь вместо отрезка
работаем с ней — снова делим пополам, находим
, и так далее
Покажем, что эта последовательность действительно задаёт число Рассмотрим её начальный участок:
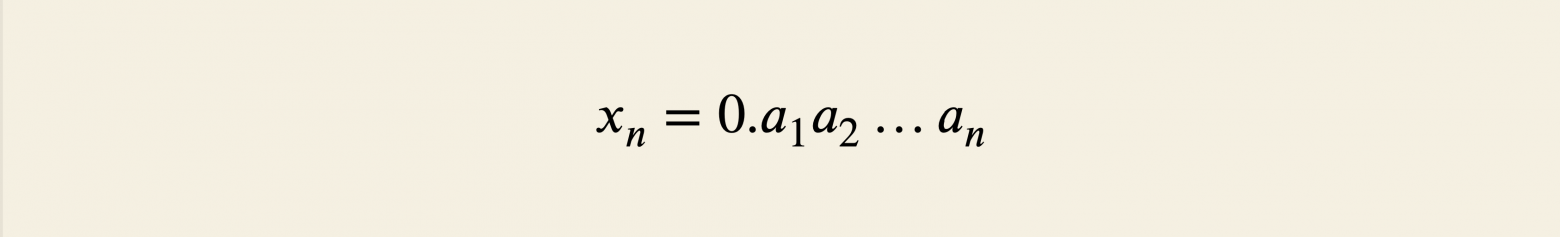
Это левая граница отрезка, полученного на шаге . Тогда:
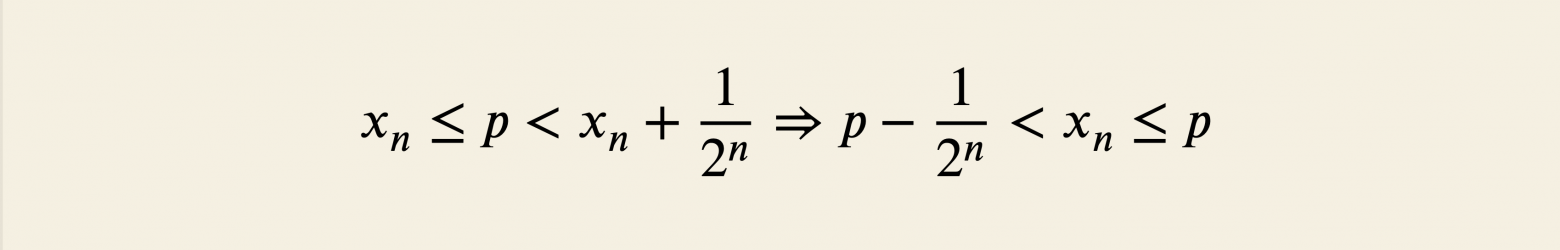
Значит, приближается к
, и последовательность задаёт число
:
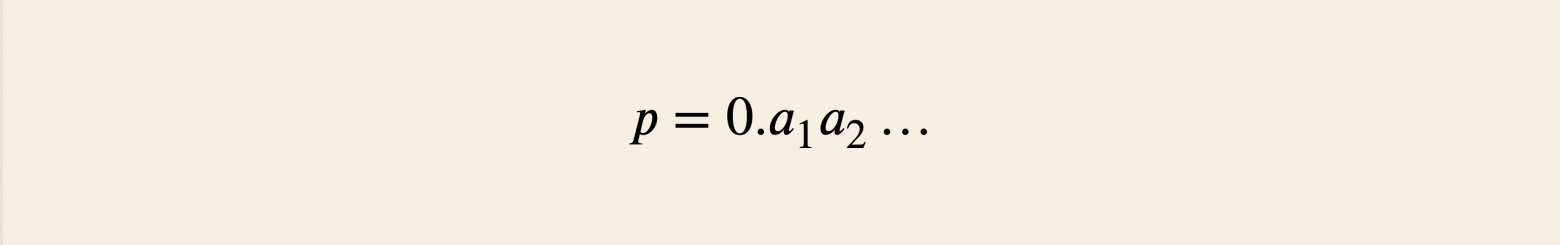
Теперь понятно, как обобщить алгоритм для любой вероятности

Алгоритм Кнута–Яо
Бросаем монету до первого орла. Пусть он выпал на -м броске. Посмотрим на
-й знак в двоичной записи
. Если это 1 — дежурит Петя, 0 — Маша и Вася
Этот алгоритм можно сформулировать и иначе — возможно, чуть проще — если использовать двоичную запись как управляющую последовательность алгоритма
Алгоритм Кнута–Яо, вторая версия. Бросаем монету до первого отклонения от управляющей последовательности. Если это орёл — дежурит Петя, если решка — Маша и Вася
Как увидеть, что алгоритм дает нужную вероятность?
Каждому набору бросков сопоставим число от 0 до 1. Для этого заменим орлы на 0, решки на 1, и получим двоичную запись числа
Например, слову соответствует число
Алгоритм Кнута–Яо сравнивает случайное число с
: если
, дежурит Петя; если
— Маша с Васей. Это можно определить в момент первого отклонения двоичных записей
и
Понятно, что Петя будет дежурить с вероятностью
Алгоритм Кнута–Яо оптимален
-
Если
не представимо в виде
, ожидаемое время работы равно
, а доказательство работает так же, как для
-
Если же
, ситуация немного меняется: алгоритм Кнута–Яо завершится не позже, чем через
бросков. Он остаётся оптимальным — и даже работает быстрее.
Подробнее про последний случай можно прочесть в Telegram-канале Кроссворд Тьюринга

Алгоритм Кнута–Яо позволяет смоделировать событие с любой вероятностью от 0 до 1. Но что делать, если исходов несколько? Например, нужно выбрать один из трёх вариантов с заданными вероятностями ? Или один из десяти?
Принцип остаётся тем же. Представим отрезок от 0 до 1, разбитый на участки длиной и
. Начинаем бросать монетку и постепенно выписывать двоичную запись случайной точки на отрезке. В тот момент, когда становится ясно, в какой из частей эта точка неизбежно попадёт, алгоритм завершает работу — и мы выбираем соответствующий исход
Тот же подход работает и для произвольного числа вариантов. Мы делим отрезок на части по заданным вероятностям и продолжаем броски, пока случайное число не попадает в одну из них однозначно

Что можно сказать про среднее число бросков в таком алгоритме? Оно зависит от формы распределения. Чем вероятности равномернее, тем больше бросков в среднем требуется; если один исход гораздо вероятнее других — алгоритм завершается быстрее
Существует важный числовой инвариант распределения, называемый энтропией — мера его неопределённости. Для трёх вероятностей энтропия вычисляется по формуле:

Вероятно, никакой алгоритм не может работать быстрее, чем энтропия распределения. С другой стороны, несложно показать, что ожидаемое время работы алгоритма Кнута–Яо не превосходит энтропию плюс два:
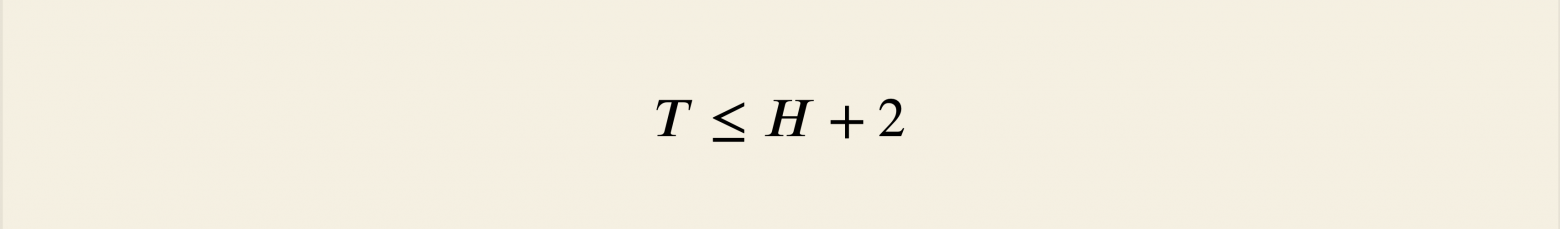
Та же оценка верна и для произвольного числа исходов. Таким образом, алгоритм Кнута-Яо оптимален с точностью до константы
На этом мы завершим историю, начавшуюся с простой задачи про монетку
Ссылки
Вот некоторые полезные ссылки
-
Питер Кэмерон A fair coin
-
Григорий Мезон, Александр Перепечко Как из монетки сделать кубик, или Любой жребий за два броска («КВАНТИК» №3, 2021 )
-
Видео версия статьи Мерзона и Перепечко
Задача
А тем, кто добрался до этого места, предлагаю такую задачку
Асимметричная монетка выпадает орлом с вероятностью
и решкой с вероятностью
. Как двум людям вытянуть честный жребий с её помощью?
Автор: d1-d5






