Как известно, бесконечности бывают разных типов. Бывают счетные, бывают несчетные. Несчетные делятся на множества мощности континуум и все остальные. Счетные множества это такие, элементы которых можно упорядочить в длинный ряд и занумеровать. С несчетными такой фокус не удается. Тогда как же можно представить несчетное множество, в частности множество вещественных чисел [0;1)? Ответ под катом.
Во-первых, под несчетным множеством далее рассматриваем множество мощности континуум, а во-вторых, ответ на вопрос из топика: геометрически интерпретировать несчетное множество можно с помощью дерева бесконечной высоты.
Как известно из википедии и других достоверных источников, мощность вещественных чисел отрезка [0;1) является континуумом, т.е. вещественные числа из этого отрезка нельзя посчитать натуральными числами. Т.е. сделать так чтобы одному натуральному числу соответствовало одно вещественное и наоборот. Для неверующих проведем упрощенную диагональную процедуру Кантора.
Представим чисела отрезка [0,1) в двоичной системе счисления и получим набор бесконечных последовательностей единиц и нулей.

Допустим, мы упорядочили такой набор в виде бесконечного списка как на рисунке. Упорядочив, получим квадратную таблицу в каждой ячейке которой находится либо 1, либо 0. Рассмотрим ячейки располагающиеса на главной диагонали.

Инвертировав диагональ(000010...) получим последовательность не попадающую в наш список, так как полученная последовательнось отличается от каждой попавшей в список хотя бы одним элементом. Последовательность номер n будет отличаться от диагональной в n-ой позиции. Следовательно, диагональная последовательность отсутствует в списке.
Исходя из приведенной схемы несчетное множество можно представлять в виде непрерывногенерируемых последовательностей. Инвертировали одну диагональную последовательность — вставили её в начало списка — сгенерировали новую и так далее. Такая карусель выглядит сомнительно.
Давайте теперь посмотрим на двоичное дерево что на следующем рисунке. Корень, наследники. В правом наследнике каждого узла — 1, в левом -0. Множество путей в дереве — пути от корня до каждого из листьев. Для дерева высоты N множество максимальных путей от вершины до листьев будет соответствовать множеству всех последовательностей нулей и единиц длины N, даже если N — бесконечность.
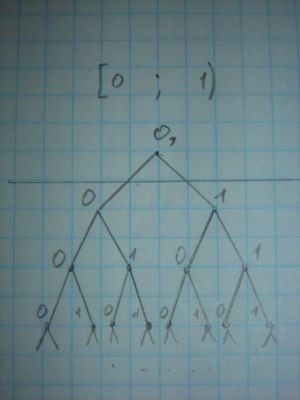
Допустим нашлась последовательность не входящая в дерево. Попробуем наложить её на один из путей дерева: 0,1,0,1 … в какой-то момент должна найтись такая развилка в которую наша последовательность не укладывается. Но из каждого узла дерева выходят либо 0, либо 1, поэтому чтобы не уложиться в путь на дереве последовательность должна содержать элементы отличающиеся от 0 или 1.
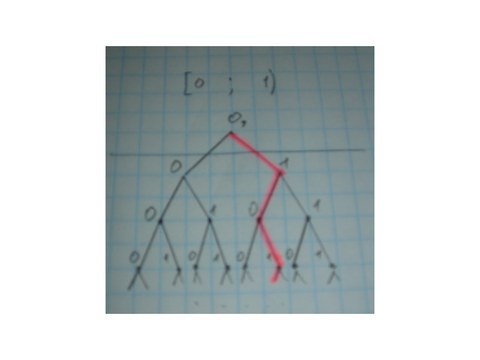
Получается, множество максимальных путей в бинарном дереве бесконечной высоты имеет мощность континуум, что эквивалентно мощности вещественных чисел отрезка [0;1).
Если вернуться к интерпретации бинарных последовательностей как двоичных дробей, то рациональные дроби вида 0,x(y) будут выглядеть в виде конечной кривулины х и бесконечной последовательности кривулин y, иррациональные числа будут выглядеть как одна бесконечная неповторяющаяся кривулина x.
В полученном результате есть одна загвоздка: Количество путей максимальной длинны, исходящих из корня двоичного дерева бесконечной высоты несчетно. Количество же вершин такого дерева можно посчитать. Это легко сделать последовательно нумеруя вершины сверху вниз (см рисунок 3).
Для дерева конечной высоты расклад другой:
Количество путей максимальной длинны, исходящих из корня в двоичном дереве высотой N равно 2^(N-1), а количество вершин почти в два раза больше — 2^N — 1. Устремляя N к бесконечности получим, что счетная бесконечность вершин в два раза “больше” несчетной бесконечности путей.
Вот такая загогулина.
Автор: korisk






