Преамбула: большинство задач в спортивном программировании оцениваются по однозначно правильному решению, по сути, сравнивая выдачу конкурсной программы с шаблоном правильного ответа. Однако существует пласт задач, где лучшее решение найти невозможно или крайне сложно в разумные временные рамки. Однако два решения легко можно сравнить между собой по некоторой метрике. Из-за этого усложняется проверяющая программа, однако, расширяется простор для разработки собственных эвристических алгоритмов решения. Представляю наш ваш суд одну такую задачу.
Комбинационные логические схемы входят в состав всех современных процессоров и других электронных средств обработки информации. Процессоры используются повсеместно и непрерывно усложняются. Количество транзисторов в современном процессоре уже превысило 2 млрд? И, похоже, рост не планирует останавливаться. Одновременно с этим уменьшаются технологически процессы производства процессоров. Транзисторы становятся все меньше и уязвимее для внешних воздействий. И вот, даже не самые сильные внешние излучения и магнитные поля могут приводить к кратковременным изменениям логических значений в микроэлектронных схемах. Эта проблема особенно актуальна в космических и других критичных к надежности системах. В данной задаче поставим вопрос: как зная логическое назначение схемы сделать её более устойчивой к внешним воздействиям? Вашей задачей будет разработать алгоритм создания такой устойчивой схемы.
Пусть задана логическая схема, без обратных связей, состоящая из следующих 6 элементов:
| Название | Описание | Операция | Изображение |
|---|---|---|---|
| INV | инвертор | OUT=!A |  |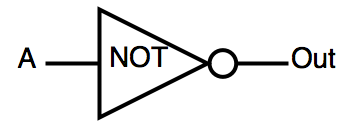
| AND | логическое «И» | OUT=A&B |  |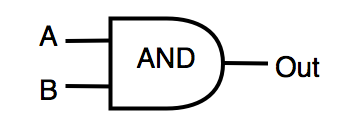
| OR | логическое «ИЛИ» | OUT=A|B |  |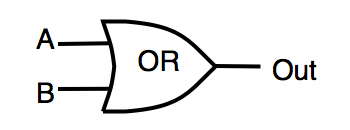
| NAND | инвертированный AND | OUT=!(A&B) |  |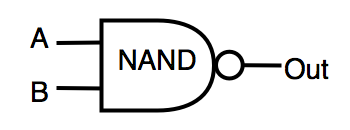
| NOR | инвертированный OR | OUT=!(A|B) |  |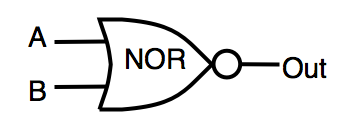
| XOR | исключающее «ИЛИ» | OUT=A^B |  |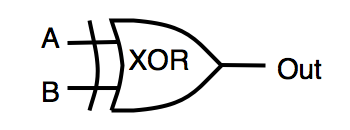
На схему воздействует шум окружающей среды, с некоторой вероятностью изменяющий логическое значение вентилей на противоположное. Необходимо сконструировать схему, которая выполняет такую же логическую функцию, что и исходная, но при этом менее подвержена сбоям. По условиям задачи схема, которую вы сконструировали, должна не более чем в “K” раз превосходить исходную по площади.
Одним из параметров, которым характеризуют устойчивость логических схем к сбоям является COF — «Общая устойчивость схемы к ошибкам». COF рассчитывается как отношение числа корректных результатов работы схемы (все выходы схемы должны иметь правильное значение) к общему числу проведенных тестов. Соответственно для максимально надежных схем COF стремится к 1.
Каждый логический вентиль схемы характеризуется следующими параметрами: S – площадь вентиля, p – вероятность сбоя в процентах при текущих внешних условиях.
Входные данные
На первой строке указано число Z – количество тестов (Z < 400). Далее следует Z тестов.
На первой строке каждого теста указано число K (2.0 ≤ K ≤ 20.0) — максимальная избыточность схемы по площади.
На следующих 6 строках указаны по два числа площадь S (1 ≤ S ≤ 100) и вероятность сбоя q (0 ≤ q ≤ 20) в процентах, параметры каждого из логических элементов в следующем порядке: INV, AND, OR, NAND, NOR, XOR.
На следующей строке указано число “I” (0 < I < 250) – количество входов схемы, затем следует I строк не более 20 символов в каждом разделенных пробелами – имена входных узлов схемы.
На следующей строке указано число “O” (0 < O < 150) – количество выходов схемы, затем следует O строк не более 20 символов в каждом разделенных пробелами – имена выходных узлов схемы.
Далее указано число логических вентилей в схеме N (1 < N < 5000), после чего следуют N строк с описанием каждого вентиля.
Описание каждого вентиля начинается с его типа далее идут имена входных узлов, далее имя выходного узла
Выходные данные
Для каждого теста необходимо вывести описание схемы в следующем формате. На первой строке число N (1 < N < 100000) – количество вентилей в результирующей схеме. Далее следует N – строк с описаниями вентилей. Описание каждого вентиля начинается с его типа далее идут имена входных узлов, далее имя выходного узла.
Начисление очков
Количество полученных очков Score суммируется по всем тестам. Количество очков полученных за тест будет равно значению COF рассчитанному для вашей схемы. Расчет COF ведется по методу Монте-Карло? в два этапа:
1) на первом этапе программа-судья определяет, что ваша схема работает идентично оригиналу. На вход обеим схемам подаются одинаковые тестовые последовательности (несколько тысяч раз) и сравниваются логические значения на выходах схемы. Если логические значения будут отличаться, то вы получите статус Wrong Answer.
2) на втором этапе программа-судья будет случайным образом по заданным вероятностям инвертировать значения на вентилях вашей схемы и сравнивать значения на вашей схеме и на схеме эталоне. Если хотя бы один из выходов будет отличаться, будет увеличиваться счетчик «неправильных ответов». Для расчета используется формула: COF = (TT — INC)/TT, где:
TT — число тестов хотя бы с одной внедренной ошибкой
INC — число тестов, где хотя бы на одном выходе схемы проявилась ошибка
Так же программа-судья проверяет, что избыточность схемы не превышает заданную.
Пример
Входные данные:
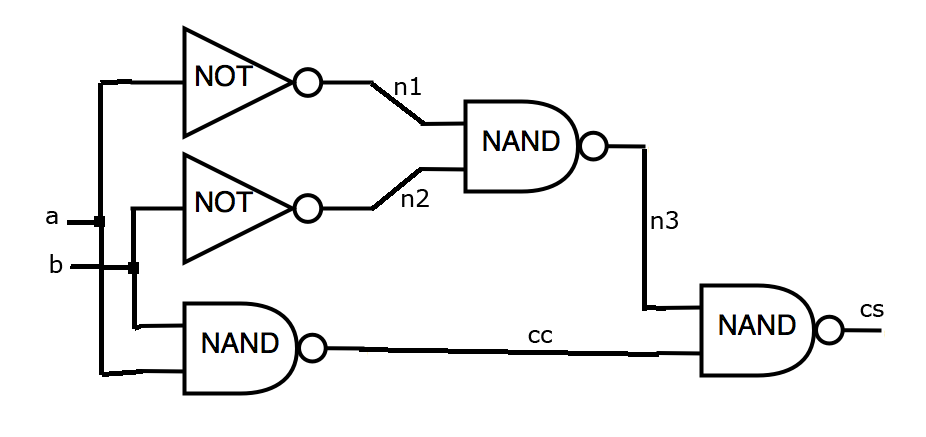
Пусть задана следующая логическая схема (см. рисунок). Требуемая избыточность не должна быть более 4.1 раз. Схема построена на библиотеке, у которой:
INV имеет площадь 50 и вероятность сбоя 3%
AND имеет площадь 60 и вероятность сбоя 3.1%
OR имеет площадь 60 и вероятность сбоя 3.2%
NAND имеет площадь 70 и вероятность сбоя 3.3%
NOR имеет площадь 70 и вероятность сбоя 3.4%
XOR имеет площадь 70 и вероятность сбоя 3.5%
Входной файл для этого задания будет иметь следующий вид:
1 5.1 50.0 3.0 60.0 3.1 60.0 3.2 70.0 3.3 70.0 3.4 70.0 3.5 2 a b 2 cs cc 5 INV a n1 INV b n2 NAND a b cc NAND n1 n2 n3 NAND n3 cc cs
Выходные данные:
Пусть наш алгоритм использует стандартный прием троирования и выбора логического значения, которое используется на большем количестве выходов (Triple Modular Redundancy (TMR))?. В этом случае выходной файл может быть записан следующим образом:
25 INV a n1_a0 INV a n1_a1 INV a n1_a2 INV b n2_a0 INV b n2_a1 INV b n2_a2 NAND a b cc_a0 NAND a b cc_a1 NAND a b cc_a2 NAND n1_a0 n2_a0 n3_a0 NAND n1_a1 n2_a1 n3_a1 NAND n1_a2 n2_a2 n3_a2 NAND n3_a0 cc_a0 cs_a0 NAND n3_a1 cc_a1 cs_a1 NAND n3_a2 cc_a2 cs_a2 AND cs_a0 cs_a1 cs_3_0_and_0_out AND cs_a0 cs_a2 cs_5_0_and_0_out AND cs_a1 cs_a2 cs_6_0_and_0_out OR cs_3_0_and_0_out cs_5_0_and_0_out cs_0_or_0_out OR cs_0_or_0_out cs_6_0_and_0_out cs AND cc_a0 cc_a1 cc_3_0_and_0_out AND cc_a0 cc_a2 cc_5_0_and_0_out AND cc_a1 cc_a2 cc_6_0_and_0_out OR cc_3_0_and_0_out cc_5_0_and_0_out cc_0_or_0_out OR cc_0_or_0_out cc_6_0_and_0_out cc
Рисунок для выходного файла
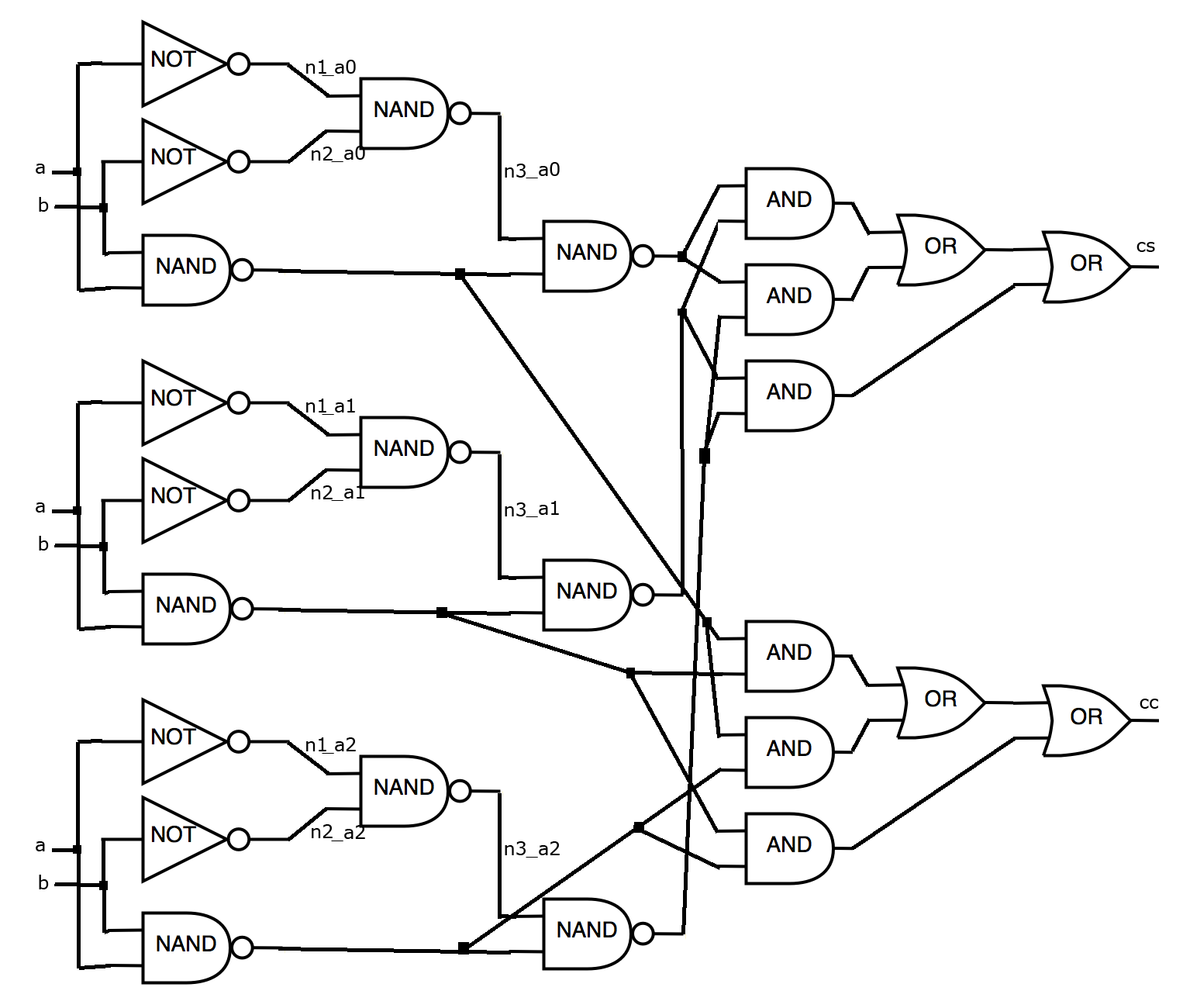
Начисление очков:
За это решение после моделирования будет начислено 0.682661 очков.
Отправка решений
Отправить решение * |
Лента отправленных решений |
Лучшие решения |
* — для отправки требуется аккаунт в системе SPOJ (Shere Online Judge) [Регистрация].
Полезные материалы
Для того что бы не писать программы с нуля можно использовать готовые наработки:
1) Простое решение задачи на CC++ — программа зачитывает данные и выводит схему как есть, без изменений.
2) Судья на CC++ — программа, которая используется на сервере для оценки решения задачи. Можно использовать локально для тестирования эффективности своих решений
3) Тестовый набор данных — набор из 102-ух тестовых схем, схожих с закрытым набором на сервере.
Автор: Turbo
