В данной статье приведу, на мой взгляд, интересное решение задачи компьютерного распознавания объектов на изображении без использования обучения.
Задача: имея фотографию многоэтажного дома попытаться определить количество этажей в нём.
Хорошую оценку для числа этажей может дать число окон по вертикали дома. Окна, балконы и другие объекты являются хорошими характеристиками этажей (особенно в жилых домах). Я буду рассматривать именно жилые дома, изображения которых легко найти в сети. Заранее следует отметить одно важное ограничение: дом на изображении должен быть показан полностью по вертикали, чтобы была возможность детектировать визуально все этажи.
Задачу рационально разбить на два этапа:
- Поиск вертикальной "полосы" окон, которые нужно будет посчитать. Две подзадачи: во-первых окна нужно искать на участке изображения, занимаемой домом, во-вторых в жилых домах окон очень много, анализировать их всех нет смысла. Необходимо выделить среди них ту вертикальную последовательность, которая лучше всего подойдёт для последующего анализа.
- Определение количества этажей (окон, или других характерных объектов) по выделенному участку дома.
Данная статься в основном посвящена первому шагу решения. Второй шаг находится ещё в разработке, однако некоторые результаты его решения также приведу.
Шаг 1. Поиск области с окнами
Основная идея заключается в том, что ряд хорошо различимых на доме выстроенных в ряд одинаковых объектов (таких как окна) создают периодическую последовательность яркости пикселей. Именно такую последовательность необходимо найти. Ниже основные этапы алгоритма.
Сначала переводим изображение в оттенки серого и масштабируем (я использовал картинки 400x600px)

Рис.1 Исходное ч/б изображение
Далее в цикле:
- Выбор на изображении относительно узкой (40px) полосы на всю высоту (Рис.2, нижнее изображение без точек)
- Осреднение яркостей по ширине полосы. Получается линия w распределения осреднённой яркости по высоте дома (Рис.2 верхний график). На ней хорошо видная периодическая структура, характерная для участка, где есть окна. Окна, расположенные в тени, менее различимы, но это не помешает.
- Вычисляется разность dw значений w и w, сдвинутых на расстояние sh. Методом перебора находится такая величина сдвига sh, чтобы добиться максимального снижения медианы разностей dw (Рис.2, нижний график).

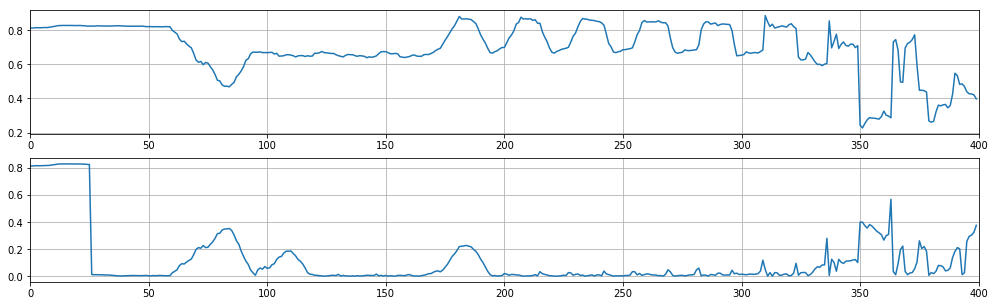
Рис.2 "Полоса" окон
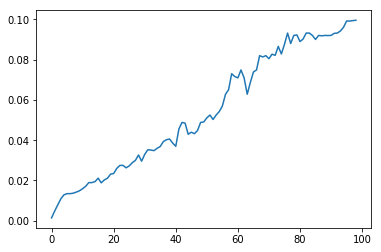
Однако, мало найти полосу изображения, на которой удалось сильнее всего снизить медиану. Дело в том, что участки с зеленью или небом, при малых величинах сдвига, могут дать большее снижение, чем окна. Но если построить зависимость величины медианы от значения сдвига для полос с окнами и без, то можно заметить ключевое отличие: при величинах сдвига, близкими высоте этажей, график с окнами имеет хорошо заметные экстремумы. Таким образом, измерять нужно не абсолютный достигаемый уровень медианы, а её максимальное снижение от максимума в процессе увеличения сдвига для каждого окна. Это ключевой момент.
| без окон | с окнами |
|---|---|
 |
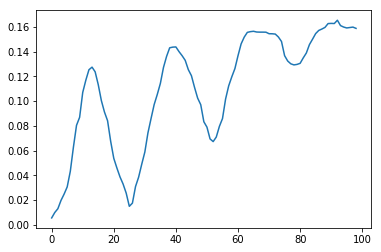 |
Рис.3 Изменение медианы осреднённой яркости в при увеличении сдвига
Ниже приведён код на python3 с комментариями.
image = Image.open("raf_data/32.jpg").resize((600,400)) #Открываем изображение.
img = np.array(image.convert("L"), dtype=float)/255
SEARCH_WIDTH = 40 # Ширина поискового окна
x_opt = [0, 1] # Здесь будут сохранены результаты: положение окна и оптимальный сдвиг
sh_range = range(1,100) # Диапозон изменения сдвига
kmax = 0
# Цикл по различным положениям поискового окна
for x in range(0, img.shape[1]-SEARCH_WIDTH, int(SEARCH_WIDTH/2)):
amax = 0
amin = 1
# Цикл по различным значениям сдвига
for sh in sh_range:
# Вычисление целевой переменной
w = img[:,x:x+SEARCH_WIDTH].mean(axis=1)
aim = (pd.DataFrame(w)-pd.DataFrame(w).shift(sh))[sh:].abs().median().values[0]
# Вычисление максимального снижения aim при данном сдвиге sh
if aim>amax:
amax = aim
amin = amax
if aim<amin:
amin = aim
aim_k = amax/amin
if aim_k>kmax:
x_opt = [x, sh, w]
kmax = aim_k
print('координата окна: {0}, оптимальный сдвиг: {1}'.format(x_opt[0], x_opt[1]))На Рис.2 отмечены точки, поставленные на расстоянии найденного сдвига. Как можно видеть, они хорошо отмечают каждое окно. Т.е. мы уже знаем высоту этажа!
Рассмотренный алгоритм неплохо находит регулярные зоны на фасадах самых разных жилых домов (Рис.4).

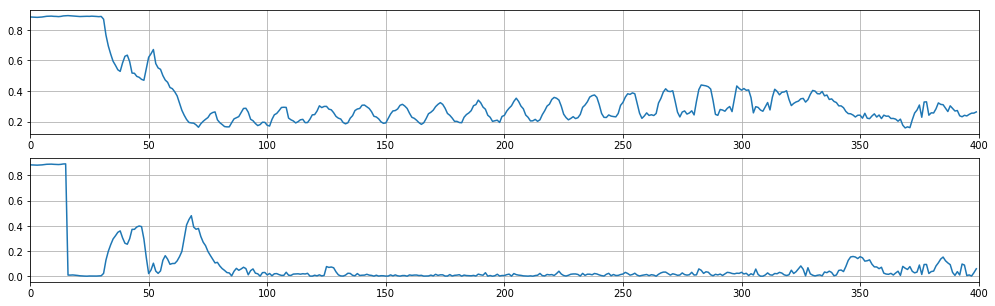

Рис.4 Пример
Шаг 2. Подсчёт числа этажей
На данном шаге начинаются основные трудности. Дальнейшие действия могут быть следующими:
- Оценить высоту дома методами обучения (задача регрессии) или без них
- В найденном на первом шаге окне искать объекты, похожие на окна, и непосредственно их считать.
Логичным кажется попробовать сначала первый способ: раз высота этажей известна, осталось определить высоту дома. Однако, схемы аналогичные приведённой на шаге 1 оказались слабо пригодными для определения высоты дома. Уменьшение высоты оптимального окна пока медиана усреднённой яркости уменьшается приводит к обрезанию большого числа окон. Поэтому сделана попытка обучить регрессионный алгоритм на собранной вручную выборке с целью определения нижней и верхней границ дома. В данном случае перспективным видится использование трёх цветов: синий должен хорошо выделять небо и верхнюю границу, зелёный подойдет для выявления нижней границы.
В отдельных случаях удаётся получить хорошие результаты, работа будет продолжена.

Рис.5 Определение высоты дома с помощью случайного леса
Автор: binrey