
Глава первая.
Искусство разумно применять светофоры
Маленькое предисловие
Каждый день, оказываясь рядом с перекрестком, мы наблюдаем одну и ту же картину, как на зеленый свет машины мчатся вперед, а на красный — они скапливаются перед светофором в длинные очереди бесполезного ожидания. Но насколько привычное является одновременно необходимым и можно ли сделать так, чтобы в своем путешествии по городу автомобилистам почти не приходилось «стоять» на красный свет? Я думаю, многие из нас слышал о мифических «зеленых волнах». Попав в такую волну и поддерживая определенную скорость, автомобилист чудесным образом будет подъезжать к каждому перекрестку как раз в то время, когда светофор горит в его сторону зеленым светом. Довольно просто организовать распространение таких «волн» вдоль одной изолированной дороги, но совсем не очевидно, можно ли это сделать на дорогах всего города сразу.
В первой главе этой статьи я построю небольшую теорию для городов с «Манхетонской» планировкой и отвечу на вопрос, как наилучшим образом регулировать на их улицах движение с помощью светофоров. Вторая глава будет посвящена возможностям применения многоуровневых развязок и магистральных шоссе.
Материал первой главы формально не требует от читателя каких либо знаний, выходящих за рамки школьной программы, хотя и предполагает некоторую культуру рассуждений, наличие карандаша и свободного вечера, возможно, не единственного. Надеюсь, что проделанная работа окажется полезной людям, проектирующим города и планирующим городское движение.
Формальное описание задачи
Представьте себе сооруженный на большом столе макет города с прямоугольными кварталами и сквозными дорогами (рисунок 1). Транспортные потоки на таком макете удобно моделировать уложенными вдоль улиц длинными узкими полосками бумаги, непрерывно скользящими, каждая в своем направлении.
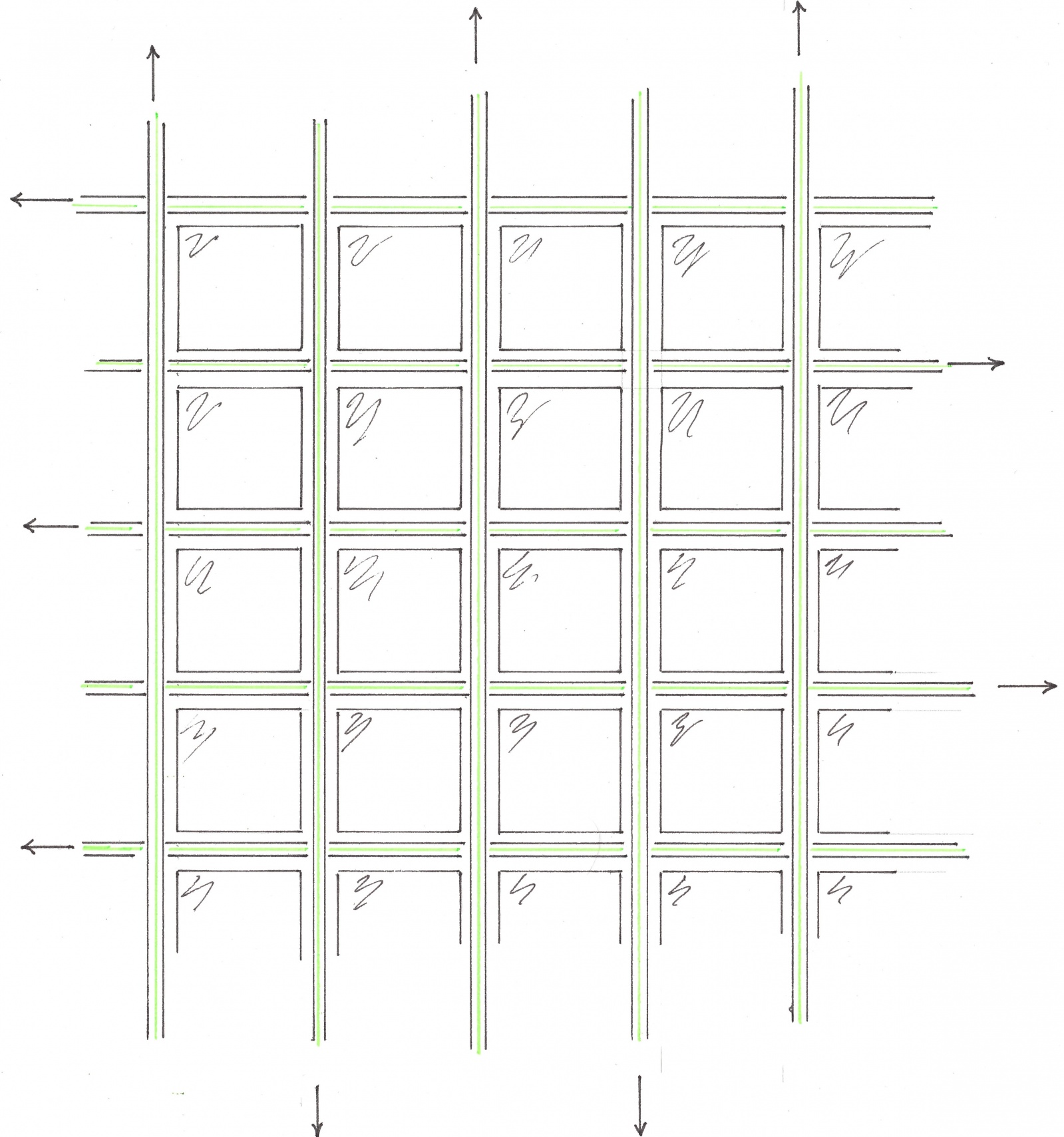
Рис. 1
На протяжении всей главы будет предполагаться, что движение потоков происходит с постоянной и одинаковой для всех скоростью. В этих условиях моделирование зеленых волн сводится к разбиению каждого потока (бумажной полоски) на белые и черные зоны и считается что автомобили могут двигаться вместе с потоком только внутри его черных зон (рисунок 2).

Рис. 2
Конфликтов в движении автомобилей заведомо удастся избежать, если не возникнет ситуации кода один и тот же перекресток оказывается перекрыт черными зонами сразу двух пересекающихся потоков.
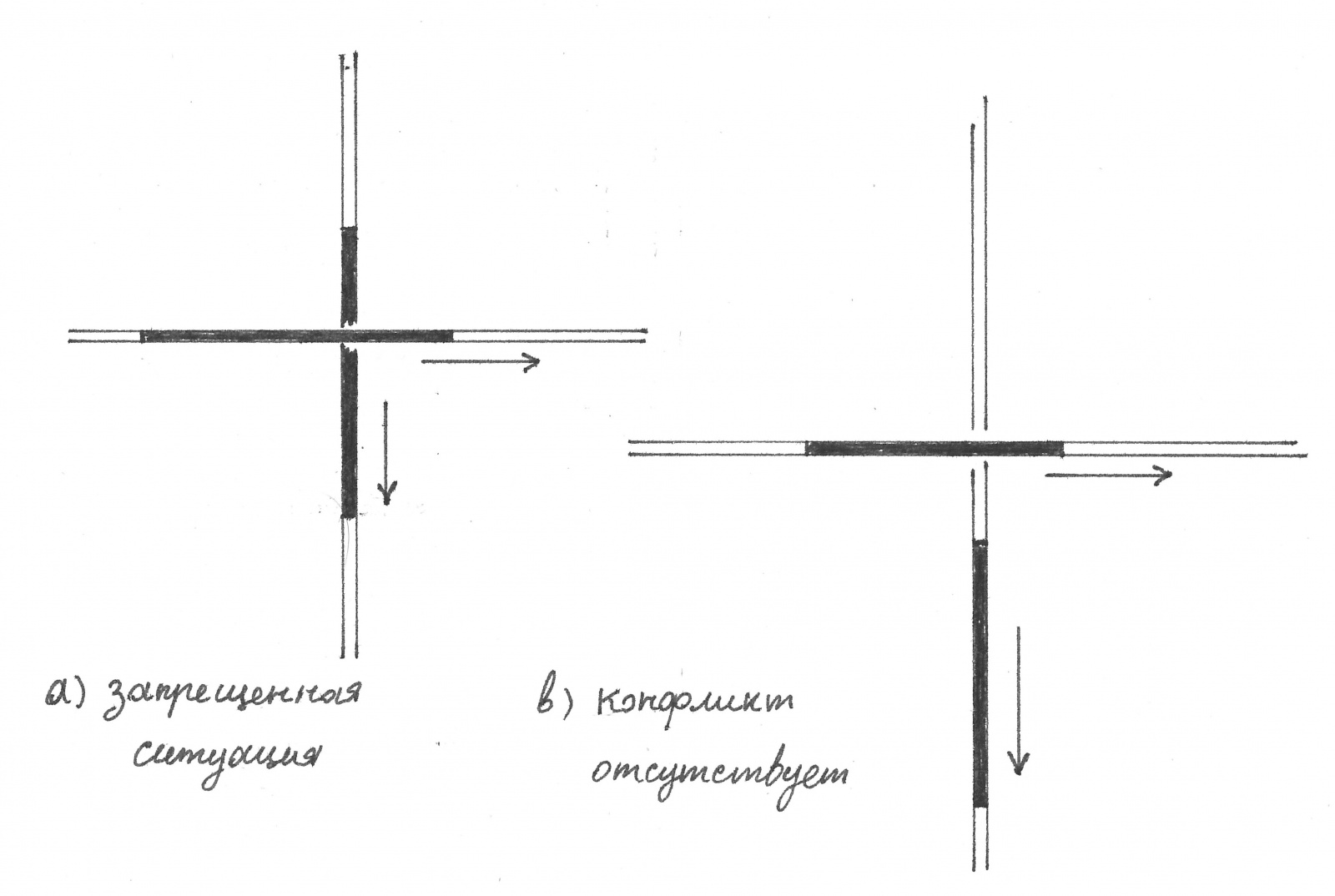
Рис. 3
В отношении к разбиениям на зоны потребуем, чтобы они были периодичны, с одинаковым для всех потоков пространственным периодом T, и чтобы на каждый такой период приходилась в только одна черная зона. На практике это требование означает, что циклы всех светофоров имеют одинаковую продолжительность и за один цикл зеленый свет в любом из направлений загорается на светофоре не чаще одного раза.
Первое из решений
Теперь у на есть все необходимые средства, чтобы попытаться отыскать (бесконфликтное) размещение «зеленых волн» на макете с квадратными кварталами. Хорошая новость: по крайней мере одно такое размещение существует и, чтобы его найти, даже не нужно строить каких-либо теорий — достаточно полчаса посидеть в кресле, покусывая карандаш. На рисунке 4a показано положение черных зон всех уличных потоков первого в этой статье бесконфликтного размещения в один из моментов времени. Стрелки указывают направления движения.
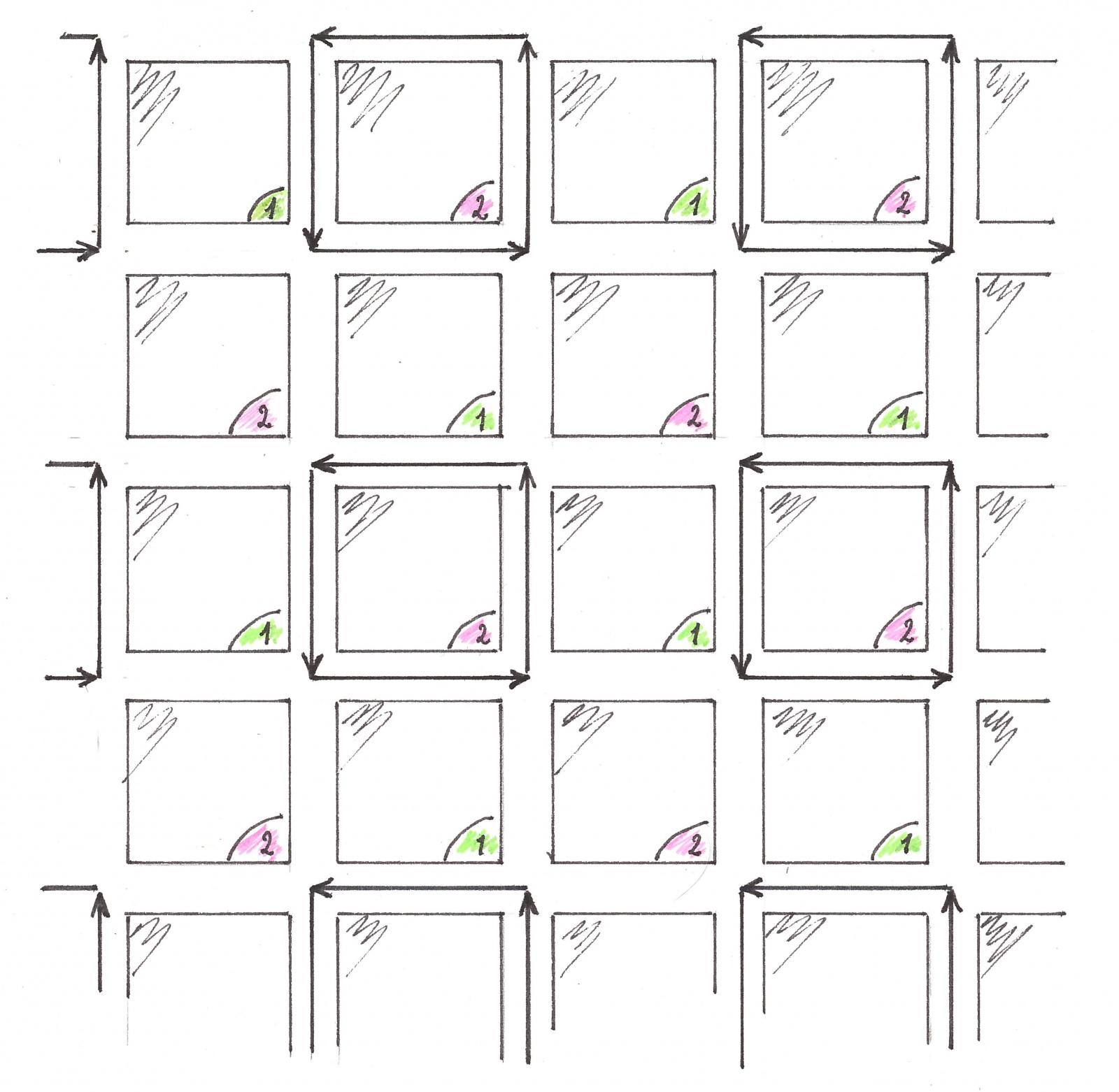
Рис. 4a
Поскольку разбиения потоков на зоны периодичны в пространстве, а скорости потоков одинаковы и постоянны, то картина, изображающая на карте города положение черных должна периодически повторяться во времени. В продолжении половины периода (временного), следующей за моментом рисунка 4a, бесконфликтному движению «стрелок » ничего не препятствует и они пройдут расстояние в один квартал, каждая. Сделав это (рисунок 4b), стрелки окажутся во взаимном расположении, детально повторяющем расположение на рисунке 4a (с точностью до зеркального отражения), таким образом доказательство бесконфликтности их дальнейшего движения можно провести простой индукцией.
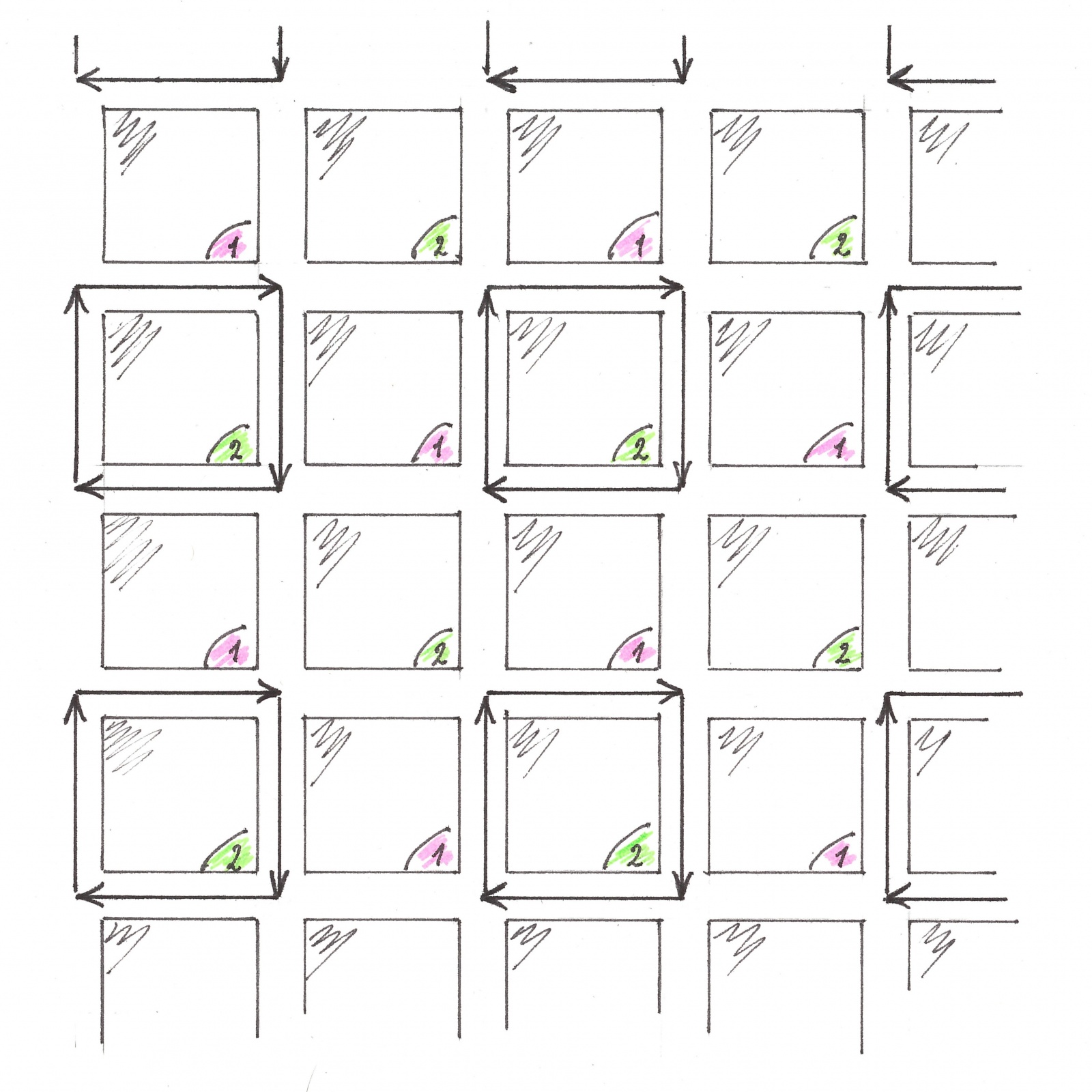
Рис. 4b
Роль светофоров, план размещения зеленых волн в городе с двусторонним движением
Что на практике должно формировать «зеленые волны», или, другими словами, — правильно проводить разбиение потоков на черные и белые зоны?
Как вы уже наверное догадались, эту роль можно возложить на светофоры. В действительности, между разбиением потоков на зоны и выбором расписания работы светофоров имеется тесная двойственная связь. Назовем работу светофора бесконфликтной, если он никогда не горит зеленым одновременно в двух перекрестных направлениях. Пусть сначала задано бесконфликтное разбиение дорожных потоков на черные и белые зоны.
Каждый раз, когда перекрестка достигает передний край очередной черной зоны какого-либо потока, заставим находящийся на перекрестке светофор загораться в направлении этого потока зеленым светом и переключаться вновь на красный в тот момент, когда ее задний край оставляет перекресток позади — этим мы построим расписание бесконфликтной работы всех светофоров. Обратно: выделив черным цветом те интервалы внутри потоков, точки которых минуют все встретившиеся им светофоры на зеленый свет, вы получите разбиение потоков на черные и белые зоны.
Если расписание, предписывало светофорам бесконфликтную работу, то и индуцированное этим расписанием разбиение тоже будет бесконфликтным. Конечно, чтобы разбиения потоков получились периодическими, с одинаковыми на всех потоках периодами и на каждый такой период приходилась только одна черная зона, на расписания светофоров придется наложит кое-какие дополнительные требования.
Для нас будет особенно важно простое следствие описанного дуализма:
Расписание, полученное по бесконфликтному разбиению потоков на зоны, индуцирует в точности то же самое разбиение
Примечательно (постарайтесь привести соответствующий пример), что симметричное утверждение уже не верно.
И так, поскольку разбиение потоков на зоны и задание расписаний светофоров — взаимозаменяемые способы описания городского движения, то для задачи поиска размещений зеленых волн мы вольны пользоваться любым из них. Обычно более наглядным и удобным является первый, но иногда, как в следующем примере, бывает полезно сочетать обе точки зрения.
Наше первое решение давало размещение зеленых волн на улицах с односторонним движением. Попробуем теперь получить его «двусторонний» вариант. Сначала заметим, что светофоры Первого решения можно поделить на две категории. Внутри каждой из категорий все светофоры работают синхронно, тогда как работа светофоров из разных категорий оказывается в противофазе. Например, в следующие пол периода, следующие за моментом, изображенным на рисунке 4a, все светофоры первой категории будут гореть зеленым для улиц, тянущихся вдоль горизонтали (относительно положения на рисунке) и красным — вдоль вертикали, а светофоры второй, наоборот, — эти же пол периода для горизонтальных улиц будут гореть красным, а для вертикальных — зеленым. Примечательно, что в описанной ситуации поворот любого светофора на 180 градусов не меняет расписания его работы.
В этом месте повествования будет удобно представлять себе макет города вместе с его светофорами и дорожными потоками, как анимированную картинку на прозрачном экране.
Пусть два таких экрана, синхронно транслирующих движение потоков Первого решения, точно наложены друг на друга. Если теперь один из экранов повернуть на 180 градусов вокруг центра какого нибудь перекрестка, то макет улиц верхнего экрана снова наложится точно на макет нижнего экрана, но при этом направления оказавшихся наложенными друг на друга дорожных потоков станут противоположными на всех совмещаемых улицах. Самым замечательным здесь оказывается тот факт, что движение потоков из разных экранов по прежнему не будет создавать конфликтов зон на совмещенных перекрестках.
Действительно, разбиение потоков на зоны что на первом, что на втором экране полностью определяется работой светофоров, но при повороте, как видно из рисунка 4a, все совмещаемые друг с другом светофоры всегда входят в одинаковые категории, и, как следствие упомянутой выше инвариантности категорий к поворотам на 180 градусов, должны работать абсолютно синхронно. После сделанных замечаний бесконфликтность движения потоков становиться следствием бесконфликтности расписания каждого из светофоров. Для тех читателей, кому мое доказательство показалось излишне запутанным, я скажу старое доброе греческое «смотри» (рисунок 5)
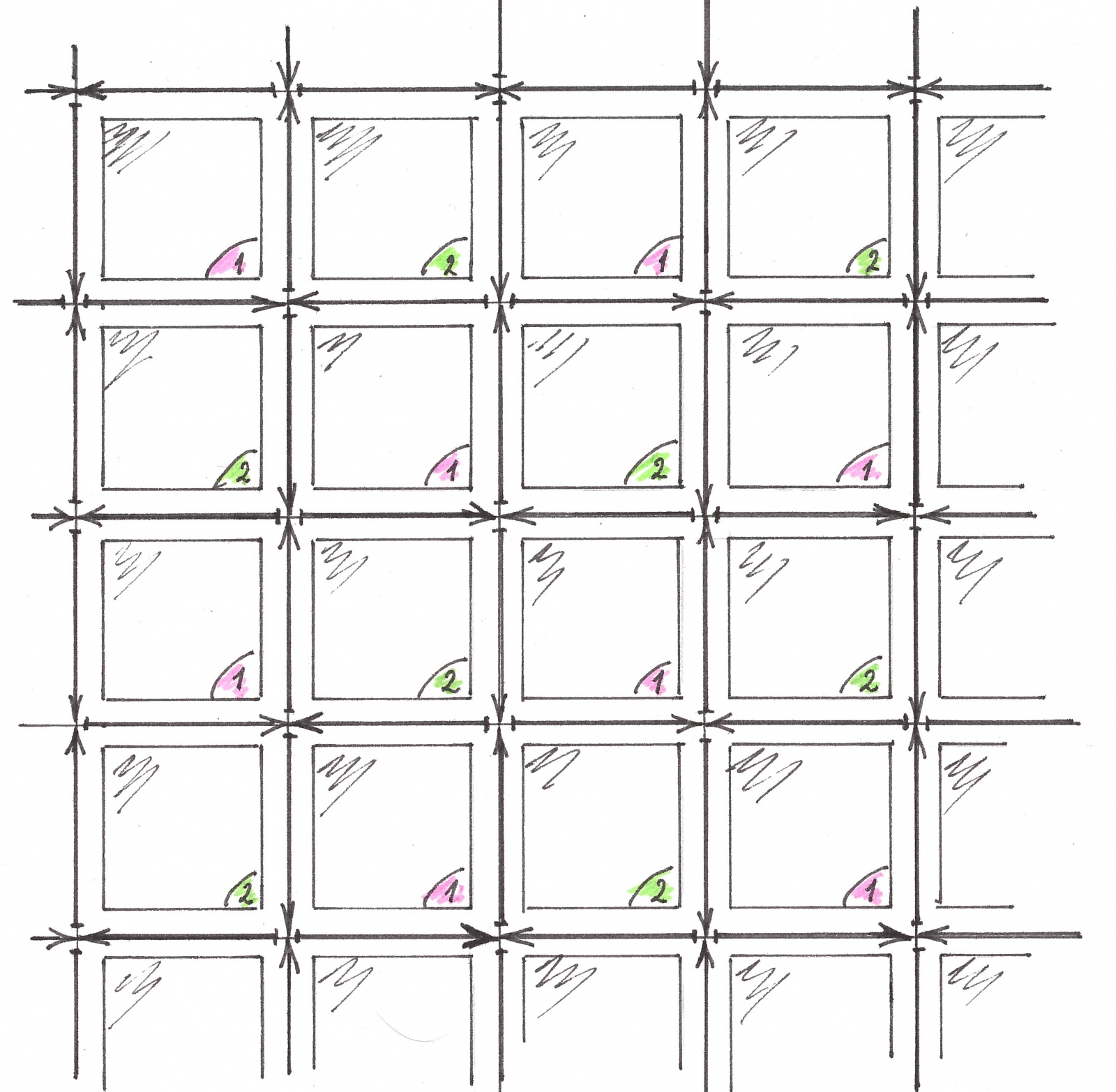
Рис. 5
Очевидные преимущества Манхетонской планировки, скрытые ограничения режима зеленых волн
И так, чем же хороши прямоугольные кварталы и дороги, простирающиеся из одного конца города в другой?
1) Объективность восприятия расстояний внутри города.
Думаю, со многими случалась одна из тех забавных ситуаций, когда целый год по сорок минут едешь от одного места до другого, а потом оказывается, что они находятся одно от другого в пятнадцати минутах ходьбы вдоль живописного сквера. В откровенно «квадратном» городе, напротив, трудно ошибиться в расстоянии между пронумерованными улицами. Отсюда вытекает
2) Простота навигации личного и схемы движения общественного транспорта.
Никаких навигаторов и мобильных приложений не нужно: между любыми кварталами всегда есть маршрут из не более чем одного участка движения по вертикали и не более чем одного участка движения по горизонтали. Если по каждой из улиц курсирует трамвай или троллейбус, то используя общественный транспорт вам не придется делать более одной пересадки за одно путешествие.
3) Экономное использование городского пространства, общая отказоустойчивость дорожной сети.
Как ни странно, но большаая площадь дорог, построенных в органически сформировавшихся городах, используется с крайне низкой эффективностью. Например, посреди множества мелких улочек, часто тупиковых, так или иначе приходится настилать две полосы асфальта, даже если автомобиль проезжает по ним только раз за четверть часа. В городах с Манхетонской планировкой такая проблема отсутствует: каждая улица дает свой небольшой вклад в общий транзит транспорта и, как следствие, нет необходимости в крупных артериальных магистралях, любая авария на которых может легко привести к потери сообщения между целыми районами.
4) Отсутствие какой-либо существенной потери времени в ожидании перед светофорами.
Для этого достаточно организовать вдоль каждой дороги режим зеленых волн. Если это сделано, то на протяжении одного путешествия потеря времени на светофороах возможна лишь в начале пути и при повороте с одной улицы еа другую.
После такой, надеюсь, хорошей рекламы Манхетонской планировки городов давайте обсудим трудности, которые приносит с собой организация уличного движения в режиме зеленых волн.
Пожалуй, самая большая из них — это ограничение, накладываемое на эффективность использования дорог, или, формально, той доли в дорожном потоке, которую занимают в нем черные зоны. Поскольку через любой перекресток единовременно проходит движение не более, чем по одной из двух улиц, использовать сразу все улицы с эффективностью большей 50 -ти процентов — невозможно. Примечательно, что в этом смысле Первое решение и его модификация для города с двусторонним движением использовали дороги с максимально возможной эффективностью.
Попробуем теперь оценить длину зеленых волн (величину пространственного периода разбиения на зоны) вообще и размер кварталов в двух уже найденных решениях в частности. По моему обывательскому опыту, удобный светофорный цикл не может иметь длительность меньше одной минуты, а комфортная скорость поездки — быть ниже 60-ти километров в час (1 км/мин). Умножив длительность цикла на скорость, получим, что длины зеленых волн любого решения должны быть не меньше 1 км. В обоих найденных нами размещениях длина кварталов составляла половину длины волны, то есть, самое малое могла равняться 500 метрам.
Кварталы длиною в 500 метров — не редкость в наших городах, хотя и комфортной для жизни такую протяженность не назовешь. В районах со сверх высотной застройкой из-за большой плотности жителей предпочтительно, чтобы каждое здание было самостоятельным кварталом.
Существует ли способ, поддерживать режим зеленых волн в транспортной сети с большой густотой расположения дорог?
Давайте в размещениях, представленных на рисунках 4 и 5, у каждого потока вычеркнем каждую вторую по порядку следования «стрелку» (можно было бы вычеркнуть каждые две из трех, или n — 1 из n). Обновленные потоки по-прежнему не будут вступать в конфликт, а длина их пространственного периода удвоиться. Теперь сожмем весь макет в два раза, как вдоль вертикали, так и вдоль горизонтали. В результате сжатия пространственные периоды зеленых вернут свою первоначальную величину, а протяженность каждого квартала уменьшится в два раза.
Хотя применение описанного трюка и позволяет неограниченно увеличивать густоту расположения дорог, оно, к сожалению, несет с собой неприемлемые издержки: коэффициент эффективности использования дорог падает пропорционально их густоте. Например, по сравнению с 50%-ной эффективностью на дорожной сети с размером квартала в 500 метров, за уменьшение размера кварталов до 250 метров придется заплатить снижением эффективности до уровня 25%, а 150-ти метровые кварталы при таком подходе будут разграничены дорогами, используемыми всего на 15%.
Само собой напрашиваются два вопроса. Первый из — них сугубо практический:
1) Как, сохраняя режим зеленых волн, увеличить плотность пролегания дорог до комфортного значения и не сильно потерять в эффективности их использования?
Второй — это скорее плод любви математиков к идеальным объектам и крайним случаям:
2) Можно ли неограниченно увеличивать плотность дорог так, чтобы эффективность использования ни одной из них не опустилась ниже некоторого (одного для всех) предельного значения?
Небольшое лирическое отступление
Проблемой оптимального светофорного регулирования я был вынужден занялся по случаю другой моей статьи, посвященной городскому транспорту, и с единственной целью — отдать исторический долг этому, как мне тогда казалось, отжившему свой век способу организации уличного движения. Когда я впервые спросил себя о значении предельного коэффициента эффективности (вопрос номер два), то готов был с кем угодно поспорить, что его величина просто обязана быть равной нулю, а всякое увеличение в сети плотности дорог непременно ведет к уменьшению эффективности применения на них режима зеленых волн, но, как это часто случается исследовательской работе, неуспех в попытке доказать ложное утверждение дал ключ к пониманию истинного положения вещей. Из оставшейся части вы узнаете о методе, который позволяет строить размещения зеленых волн как на сетях, интересных с точки зрения практического применения, так и на нереалистичных сетях со сколь угодно большой плотностью расположения дорог. В конце этой главы я оставлю вам открытую проблему, с которой мне так и не удалось справиться, а сейчас попрошу уделить внимание одной маленькой и изящной теории.
Полосы затенения
На рисунке 6 в три различных момента времени изображены два вертикальных и один, пересекающий их, горизонтальный поток. Как уже было сказано, скорости всех потоков предполагаются одинаковыми, а движение — не приводящим к конфликтам между их черными зонами. Фрагмент A горизонтального потока, будучи черным, запрещает тем самым оказаться черными фрагментам B и C вертикальных потоков.
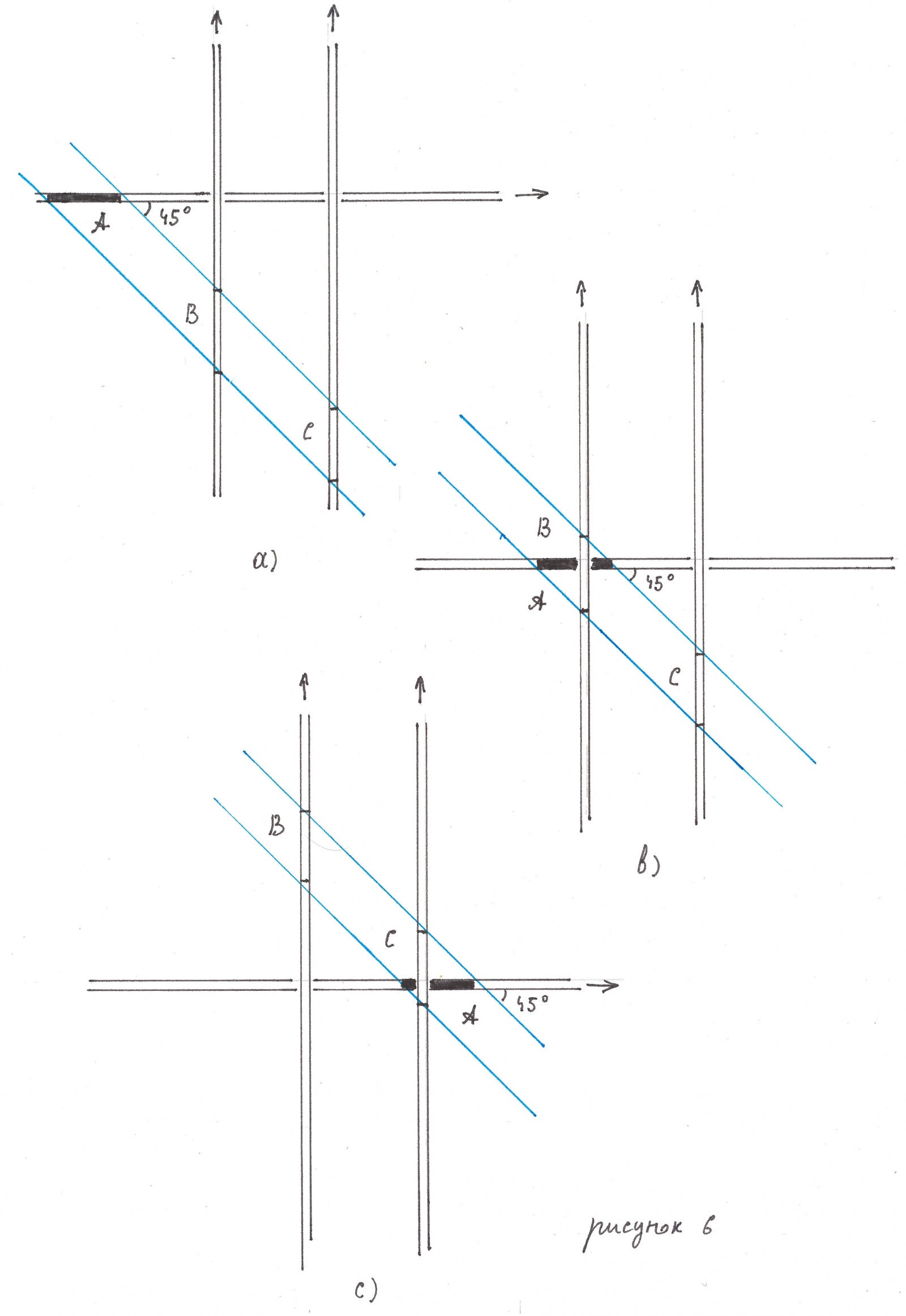
Свяжем с фрагментом A движущуюся синхронно с ним наклонную полосу, граничные прямые которой образуют с вертикалью рисунка угол в 45 градусов. По аналогии с тенью, которую бы отбрасывал A в косых лучах солнца, будь он непрозрачным предметом, назовем эту полосу «теневой». Как видно из того же рисунка, область пересечения связанной с A теневой полосы и любого вертикального восходящего (направленного вверх) потока остается относительно последнего абсолютно неподвижной и, самое главное, не может быть черной.
С каждым черным сегментом любого горизонтального потока, на самом деле, стоит связать сразу две теневые полосы: одна из них окажется наклоненной в сторону движения сегмента (как дерево наклонено в сторону дуновения ветра), а другая — навстречу ему. Полосы первого типа договоримся называть «красными», а второго — синими (рисунок 7).
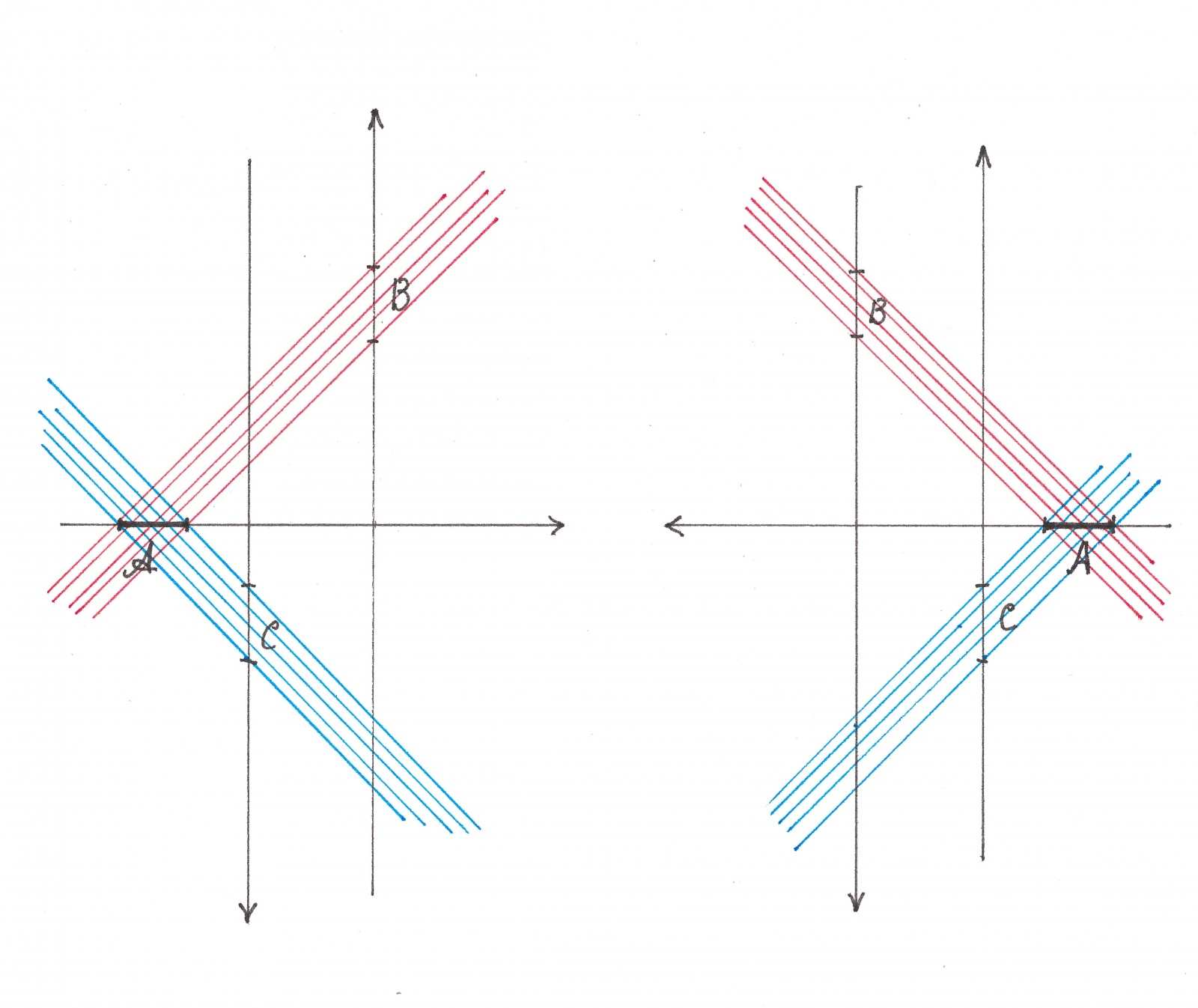
Рис. 7
Роль красных и синих теневых полос в создаваемой теории определяется их свойствами: ни один сегмент восходящего потока, попавший в «затенение» хотя бы одной синей полосы, и ни один сегмент нисходящего потока (вертикального потока, направленного вниз), попавший в затенение хотя бы одной красной полосы, не должны быть черными.
Давайте теперь посмотрим, как в общем случае выглядит совокупность всех теневых полос, например, красного цвета какого-нибудь горизонтального потока (рисунок 8).
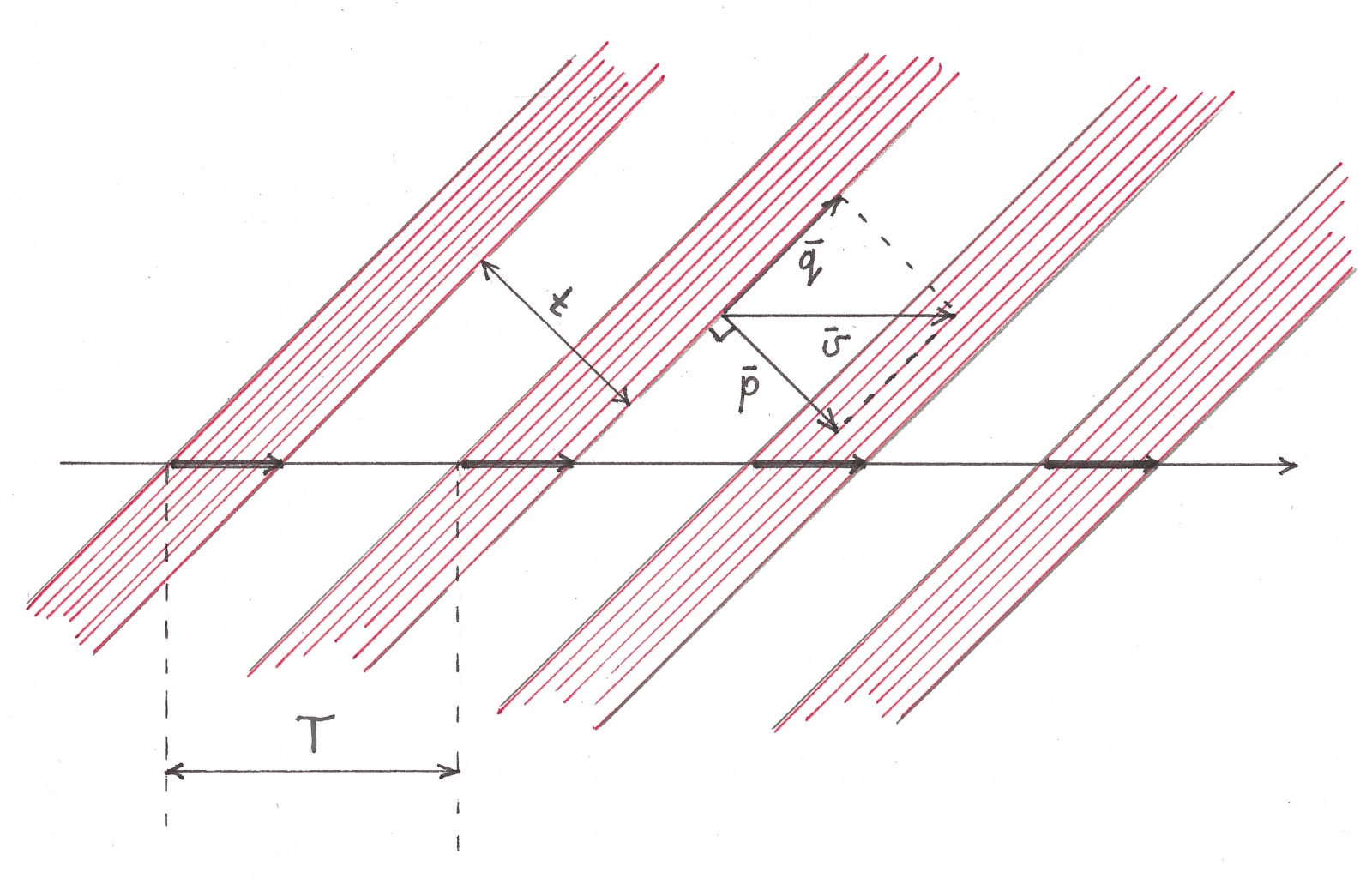
Рис. 8
Располагаясь вдоль потока T-периодично, его черные зоны порождают периодический линейчатый узор из параллельных полос одинаковой ширины. Точнее говоря, этот узор T-периодичен (полностью совмещается с самим собой при сдвиге на расстояние T) в горизонтальном направлении, периодичен с периодом t = T/√2 в направлении
(общей) нормали к границам своих полос и «выдерживает» любое смещение параллельно самим полосам. Интересно понаблюдать за тем, как весь узор вместе с потоком движется вправо. Перемещение каждой отдельной полосы (вектор ʋ) можно представить в виде векторной суммы ее смещения вдоль себя (вектор q) и одновременного движения в направлении, перпендикулярном своей границе (вектор p). Как вы догадываетесь, нашему зрению трудно заметить движение бесконечной полоски тени вдоль себя, если таковое вообще имеет какой-либо смысл, кроме формального, поэтому складывается иллюзия, что узор движется не вправо вместе с потоком, а в перпендикулярном к границам своих полос направлении, перемещаясь относительно рисунка по диагонали вправо вниз. По законам геометрии скорость движения переднего фронта каждой полосы оказывается ровно в √2 раз меньше скорости черной зоны, с которой она связана.
Кстати, на этом же явлении скорее всего основано применение стреловидных крыльев в сверхзвуковой авиации: движение воздуха параллельно самому крылу на подъемную силу никак влиять не должно, а нормальная составляющая скорости, с которой сверхзвуковой поток попадает на его переднюю кромку, из-за угла стреловидности оказывается меньше скорости звука, давая возможность крылу работать в комфортном для него дозвуковом режиме.
Описание иллюзии позволяет сделать вывод, что следующие три вида движения выглядят неотличимо для любой красной теневой полосы, и поэтому могут рассматриваться, как эквивалентные:
* движение вдоль горизонтали вместе с потоком со скоростью ʋ;
* движение вдоль диагонали рисунка вниз со скоростью ʋ/√2;
* движение вдоль вертикали вниз со скоростью ʋ.
После замены слова «вниз» на слово «вверх» все сказанное о свойствах движения красных полос и красных линейчатых узоров становится справедливым и по отношению к движению синих.
Глобальные полосы и линейчатые узоры
Пусть на некоторой дорожной сети задано какое-либо размещение зеленых волн. Теневые полосы одного и того же цвета, относящиеся к движущимся в одну сторону потокам, обязательно параллельны друг другу, но могут как стоять особняком, так и частично или даже полностью быть наложенными друг на друга (рисунок 9). Поскольку их движение направлено в одну и ту же сторону и имеет одну и ту же скорость, то относительно друг друга эти полосы остаются абсолютно неподвижными. Совместим полосы одного цвета сразу всех движущихся в одном направлении (горизонтальных) потоков. В результате наложения пересекающиеся теневые полосы разных потоков сольются, образуя глобальные теневые полосы. Новые полосы также будут параллельны друг другу, вместе образуя глобальный линейчатый узор.
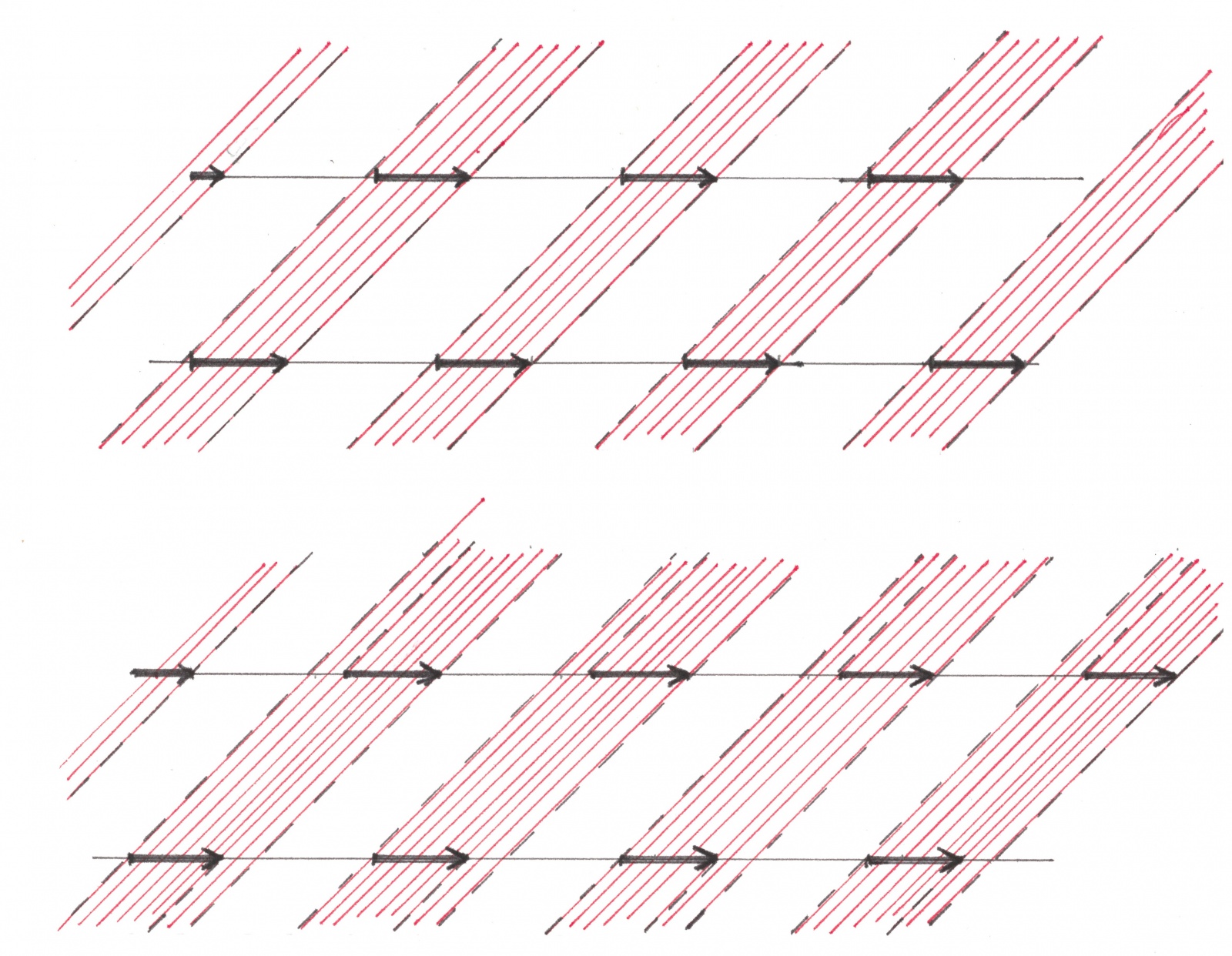
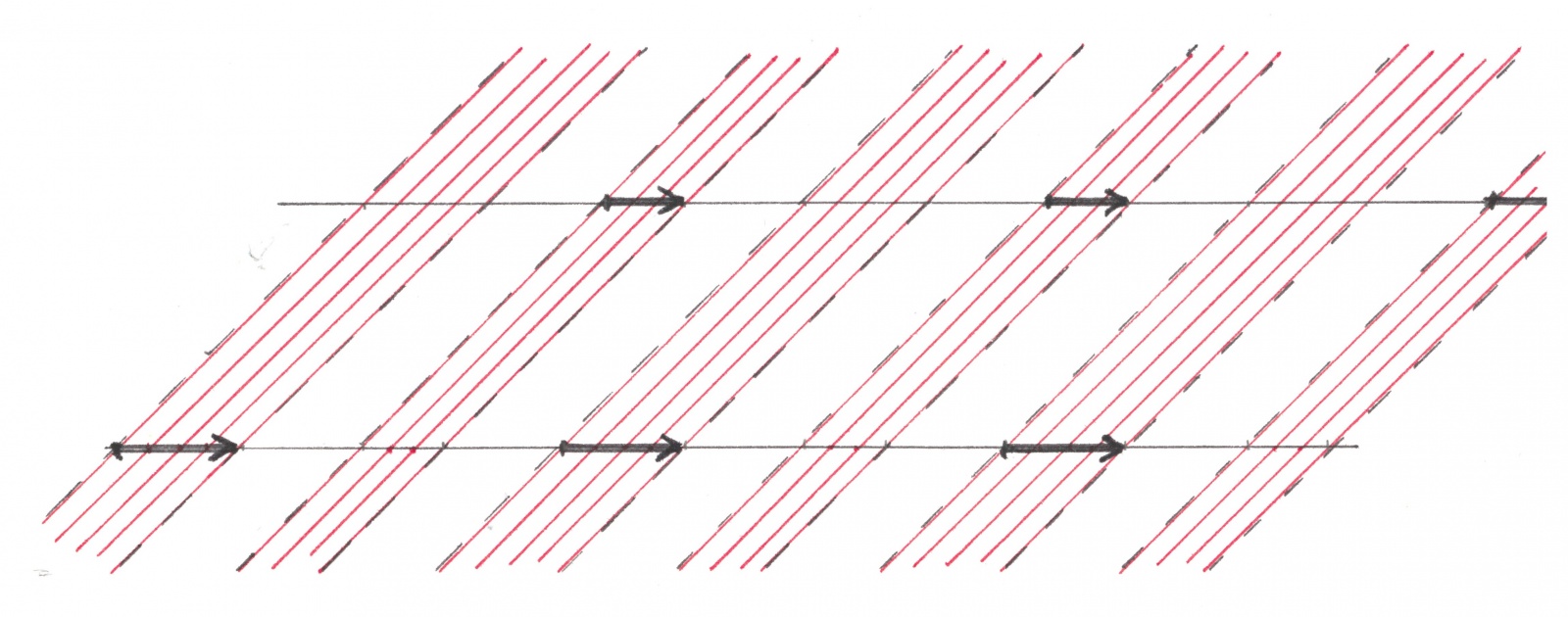
Рис. 9
Глобальный линейчатый узор t-периодичен вдоль одного из диагональных направлений макета и выдерживает любое смещение вдоль другого, так как все линейчатые узоры отдельных потоков, из которых он был образован, обладали этим свойством. По тем же причинам глобальный узор T-периодичен в горизонтальном и в вертикальном направлениях, хотя T вдоль этих направлений уже может не быть его наименьшим периодом.
Всего формируется четыре глобальных линейчатых узора, различающихся цветом и наклоном полос: составленный из красных правых, красных левых, синих правых и синих левых. На рисунке 10a совмещены все глобальные узоры, порожденные потоками рисунка 4a, а на рисунке 10b — их положение спустя четверть (
временного) периода.

Рис. 10a
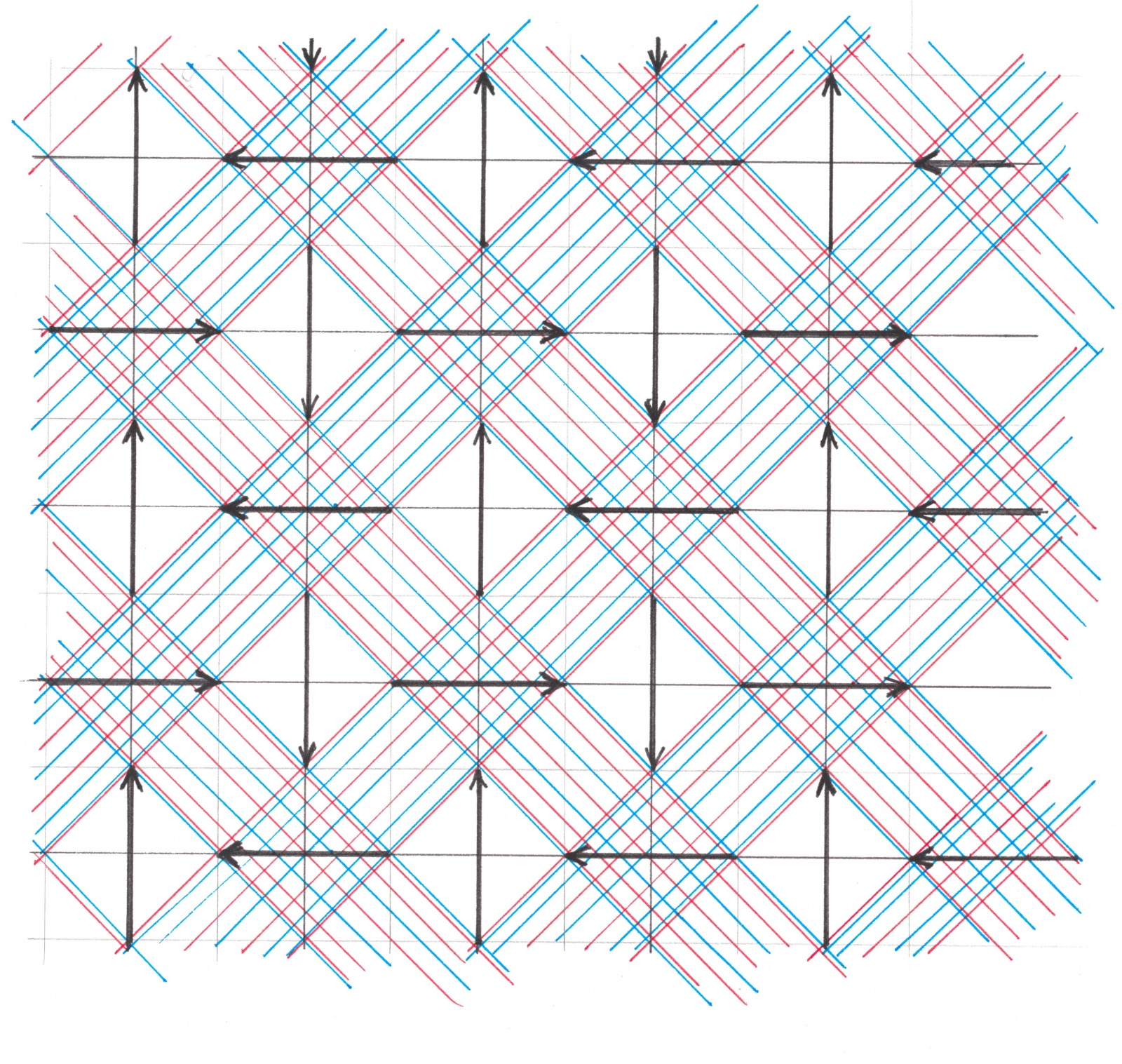
рисунок 10b
Характерной особенностью обеих иллюстраций является закономерность между расположением стрелок и различных цветовых зон: стрелки вправо оказываются всегда на пересечении правых красных и левых синих полос, стрелки влево — левых красных и правых синих, стрелки вверх лежат исключительно внутри зон, свободных от красных теней, а стрелки вниз — внутри зон, свободных от синих. Объяснение этому наблюдению содержится в самом правиле построения теневых полос.
Клетчатые узоры
Любая пара линейчатых узоров, теневые полосы которых вытянуты вдоль разных диагоналей рисунка, представляет из себя клетчатый узор, наподобие рисунка на шотландском килте, скатерти в прованском стиле или вашей офисной рубашке. У клетчатых узоров есть простые и одновременно полезные для нашего исследования свойства, давайте их рассмотрим.
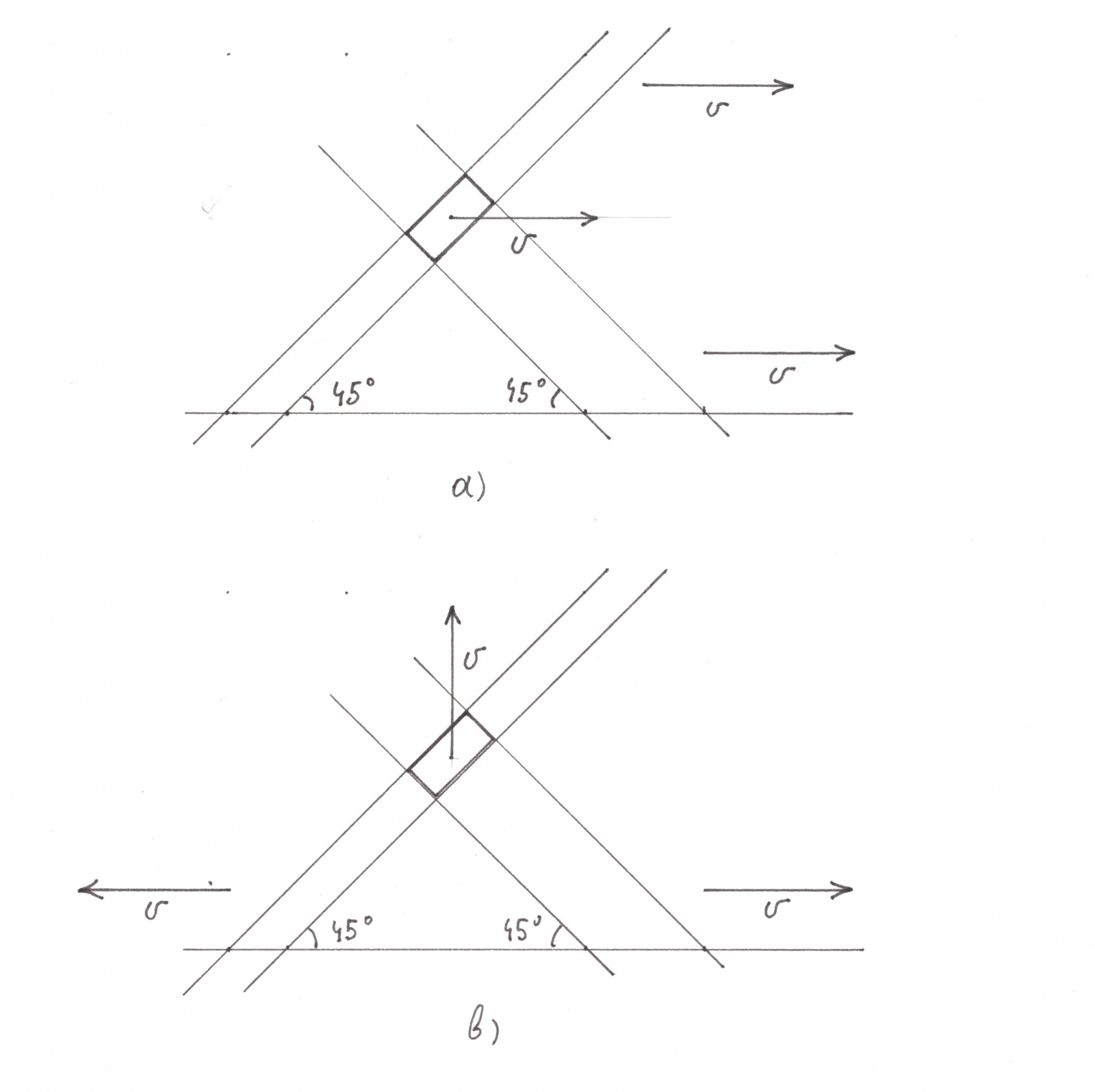
Рис. 11
Если две диагонально расположенные теневые полосы движутся в одном направлении с одинаковой скоростью ʋ, то, очевидно, прямоугольник, являющийся областью их пересечения, движется в том же направлении со скоростью ʋ (рисунок 11a). Пусть теперь движение этих полос происходит вдоль горизонтальной прямой с равными по величине скоростями ʋ, но в противоположных направлениях.
Здесь возможны два случая: обе полосы движутся в либо в сторону своего наклона (как все красные глобальные полосы), либо в против него (как все синие глобальные полосы). В первом случае движение каждой из них не отличимо от вертикального движения вниз, куда и перемещается со скоростью ʋ прямоугольная область их пересечения. Второй случая полностью подобен первому, но с тем отличием, что область пересечения движется вертикально вниз.
Еще одно важное свойство клетчатых узоров — унаследованная периодичность как по диагональным направлениям, так и вдоль главных осей. Пусть клетчатый узор образован пересечением двух диагональных линейчатых узора, первый из которых p-периодичен вдоль северо-восточного направления, а второй q-периодичен вдоль северо-западного. В такой ситуации сам клетчатый узор будет p-периодичен вдоль северо-восточного, q-периодичен вдоль северо-западного направлений и может быть представлен как прямоугольная мозаика из клеток размера p × q (рисунок 12). Если p = q = T/√2, то этот узор еще и T-периодичен по вертикали и по горизонтали.
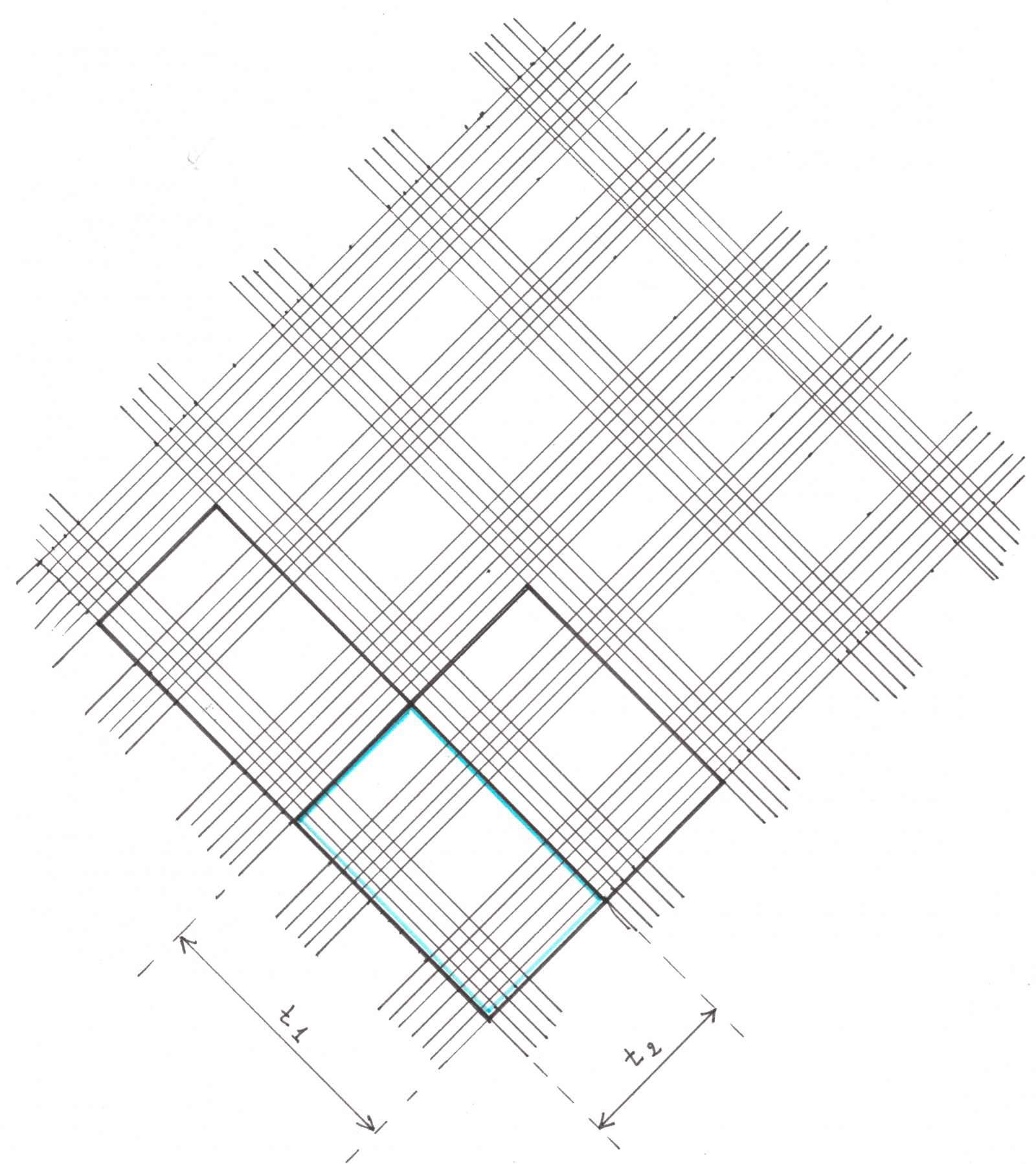
Рис. 12
Синхронность движения клетчатых узоров и зеленых волн
Как уже было сказано, с любым периодическим размещением зеленых волн ассоциированы четыре клетчатых узора: красно-синий — на пересечении правых красных и левых синих глобальных полос, сине-красный — на пересечении правых синих и левых красных глобальных полос, и два симметричных — красно-красный и сине-синий.
Если все дорожные потоки движутся со скоростью ʋ, то результаты предыдущего параграфа в приложении к ассоциированным клетчатым узорам означают, что красно-синий узор движется со скоростью ʋ по горизонтали вправо, сине-красный — со скоростью ʋ по горизонтали влево, красно-красный и сине-синий узоры со скоростью ʋ движутся строго вертикально, первый — вниз, а второй — вверх.
Из последнего можно заключить, что движение черных зон дорожных потоков, обозначаемых на рисунках стрелками, и клеток, соответствующих зонам клетчатых узоров, оказываются синхронизированными. Так, любая стрелка вправо движется все время внутри красно-синего прямоугольника, оставаясь при этом неподвижной относительно его границ, любая стрелка влево находится в подобном отношении с некоторым сине-красным прямоугольником, любая стрелка вверх — с бело-белым прямоугольником сине-синего узора, а любая стрелка вниз — с бело-белым прямоугольником красно — красного узора.
Синхронность движения стрелок и клеток открывает принципиальную возможность использования клетчатых узоров для построения зеленых волн.
Обратное конструирование
Лемма о порождении
Пусть на плоскость нанесена сеть из горизонтальных и вертикальных прямых с указанным на них направлением, обозначающих дорожные потоки. Пусть, также, задано положение двух исходных диагональных клетчатых узоров: красно-красного и сине-синего, каждый из которых t-периодичен вдоль направлений протяженности своих полос.
Существует канонический (стандартный) способ построить размещение зеленых волн на упомянутой сети, у которого:
*) черные зоны каждого потока, расположены на нем T-периодично (T = t × √2);
**) в нулевой момент времени ассоциированный с размещением красно-красный глобальный узор будет целиком содержаться внутри исходного красно-красного узора, а глобальный сине-синий — внутри исходного сине-синего (под понятием «клетчатому узору A содержаться внутри клетчатого узора B» понимается требование, чтобы каждая полоса, входящая в узор A, лежала целиком внутри какой-нибудь полосы узора B);
Сразу отметим T-периодичность исходных узоров вдоль горизонтального и вертикального направлений (смотрите предыдущий параграф). Скрестив правые (наклоненные вправо) полосы одного из исходных узоров с левыми полосами другого, мы тем самым выделим два производных клетчатых узора: сине-красный и красно-синий. Производные узоры также будут t-периодичными вдоль обоих диагональных направлений плоскости, а значит, и T-периодичными вдоль ее вертикальных и горизонтальных прямых. Как следствие, интервалы, на которые оказывается разбита всякая вертикальная или горизонтальная прямая своим пересечением с клетками любого из исходных или производных узоров, заполняют эту прямую с T-периодичной регулярностью.
На каждом направленном вверх потоке среди интервалов, по которым поток пересекается с бело-белыми клетками сине-синего исходного узора, возьмем какой-нибудь интервал с максимальной длиной. При смещении выбранного интервала на величину кратную T вверх или вниз он снова совместится с областью пересечения его потока и бело-белой клетки сине-синего узора. Давайте все такие области и считать черными зонами направленных вверх потоков (рисунок 13).
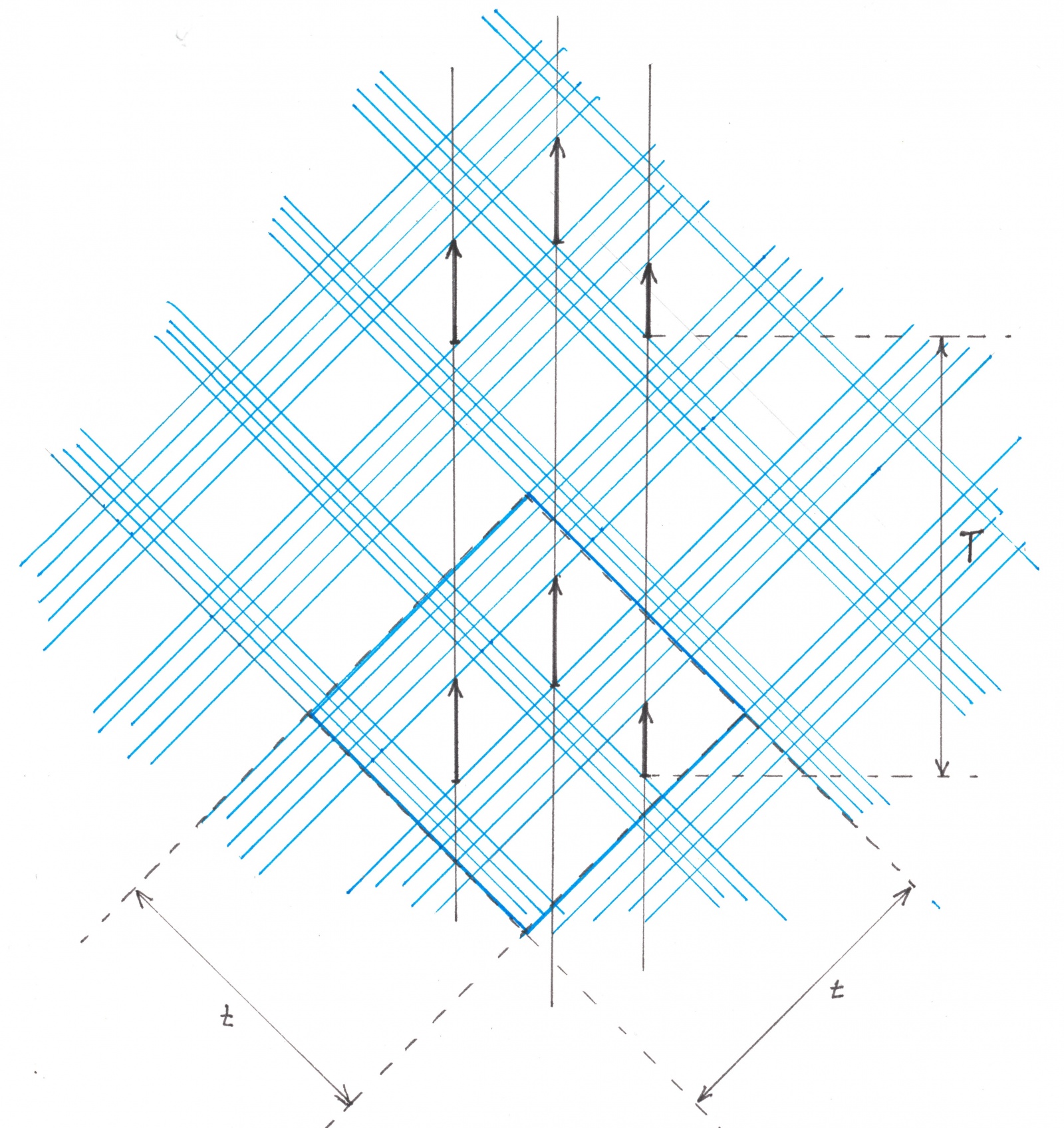
Рис. 13
Чтобы построить черные зоны на потоках, направленных вниз, нужно описанную только что процедуру проделать по отношению к интервалам их пересечения с бело-белыми клетками красно-красного исходного узора, для потоков вправо — по отношению интервалам их пересечения с красно-синими, а для потоков влево — с сине-красными клетками производных узоров.
Все потоки теперь разбиты на зоны, осталось показать, что во время движения между ними не возникнет конфликтов.
В нулевой момент времени между потоками конфликты отсутствуют по правилу запрета цветов: черные зоны горизонтальных потоков, размещаясь внутри красно-синих и сине-красных клеток, не могут находится в пересечении с черными зонами потоков, направленных вверх, поскольку те лежат в клетках, свободных от синего цвета, ровно как и не могут находится в пересечении с черными зонами потоков, направленных вниз, потому как последние находятся внутри клеток, свободных от красного цвета.
Придя в движение, зоны всех потоков по условию должны иметь одну и туже скорость ʋ. Заставим красно-красный исходный узор двигаться со скоростью ʋ вниз, а сине-синий — с этой же скоростью, но вверх. Перемещение исходных узоров заставит красно-синий производный узор двигаться вдоль горизонтали со скоростью ʋ вправо, а сине-красный — точно так же, но влево. Получается, что черные зоны потоков будут двигаться синхронно с теми клетками цветных узоров, внутри которых они изначально и были построены, а значит, доказательство основанное на правиле запрета цветов можно повторить для любого момента времени.
Важным свойством процедуры канонического построения размещений является ее «инволюнтность»: если применить ее к дорожной сети и клетчатым узорам, ассоциированным с некоторой схемой движения, то в итоге получиться та же самая схема.
Читателю предлагается самостоятельно доказать вторую:
Лемма об оптимальности канонически построенных размещений
Среди всех размещений зеленых волн, удовлетворяющих требованиям *) и **) леммы о порождении, не найдется ни одного, которое было бы эффективнее канонически построенного размещения хотя бы на одном потоке.
Одна из перспективных схем движения в районах с высотной застройкой
Ранее был описан способ, как из двунаправленного схемы движения рисунка 5, с размером кварталов в пол периода (500 метров) и 50-ти процентным уровнем эффективности использования каждой дороги, вычеркивая каждую вторую стрелку в каждом потоке, получить схему движения с коэффициентом эффективности в 25% и размером кварталов в четверть периода (250 метров).
С помощью одного хитрого вида клеточных узоров и Леммы о порождении мы сейчас построим размещение зеленых волн с тем же значением эффективности в 25% использования дорог, но на сети с размером кварталов всего в 1/8 периода (125 метров). Такая высокая плотность расположения дорог может быть предпочтительна в частях города, застроенных преимущественно небоскребными зданиями, которые, как известно, по числу приходящихся на них человек и количеству автомобилей вполне сопоставимы с целыми кварталами в традиционных районах.
На рисунке 14а изображены «элементарные» фрагменты упомянутых узоров, а на рисунке 14b они оба одновременно наложены поверх дорожной сети, позволяя нам бесконфликтно разбить ее потоки на черные и белые зоны.
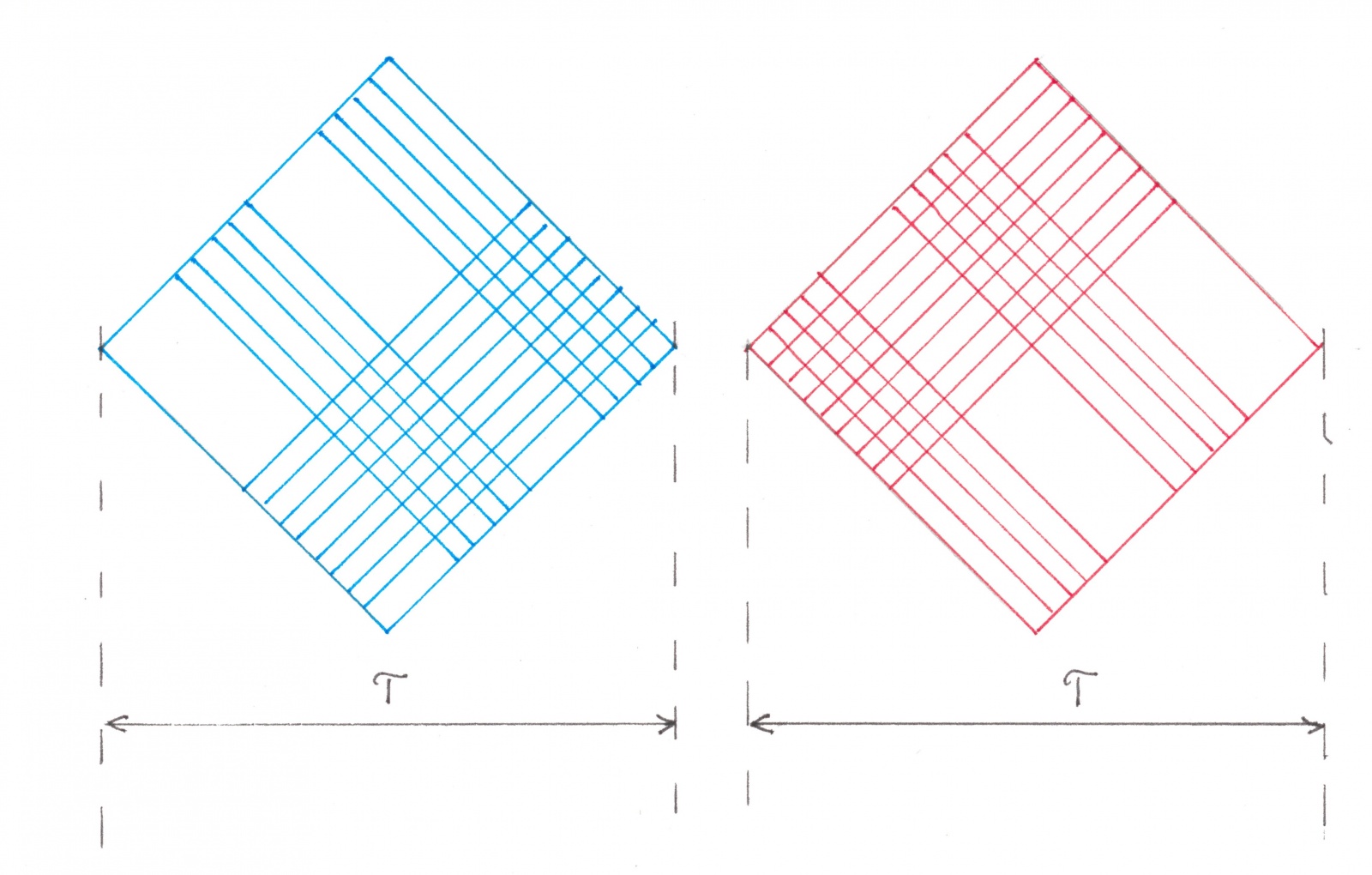
Рис. 14a

Рис. 14b
Предложенная к использованию дорожная сеть при желании может быть пополнена любым количеством горизонтальных и вертикальных потоков (дорог), причем Лемма о порождении гарантирует возможность на новых дорогах так разместить зеленые волны, что они не будут вступать в конфликт ни друг с другом, ни с зелеными волнами на потоках, присутствовавших в сети изначально.
Постарайтесь определить, какие положения новых дорог, позволят при выбранном направлении движения использовать их с эффективностью в 25%, а для каких — эта величина окажется существенно меньше. Найдите положения, в которых эффективность использования дорог окажется равной нулю.
Предельно эффективные схемы дорожного движения
Повсеместному применению описанной в предыдущем параграфе схемы движения, несомненно, будет препятствовать ее относительно низкая эффективность использования дорог: в два раза ниже теоретически достижимого уровня в 50%. Естественно тогда задать вопрос:" Какими могут быть схемы дорожного движения, поддерживающие режим зеленых волн, и использующие каждую дорогу с 50-ти процентной эффективностью". Всякую такую схему движения будем называть предельно эффективной.
Сейчас будет описан общий метод, позволяющий построить все предельно эффективные схемы дорожного движения, а в конце параграфа — отдельно вычерчены те из них, которые являются наиболее перспективными для применения на практике.
Пусть дана какая-нибудь предельно эффективной схема движения.
Из требования T-периодичности вытекает, что каждый ее поток оказывается составленным из чередующихся белых и черных зон одинаковой величины, равной T/2. В рассматриваемой схеме движения, как и в любой другой, обязательно присутствует хотя бы один горизонтальный поток, движущийся вправо. Связанный с этим потоком линейчатый узор из красных теневых полос должен выглядеть как на рисунке 16a.
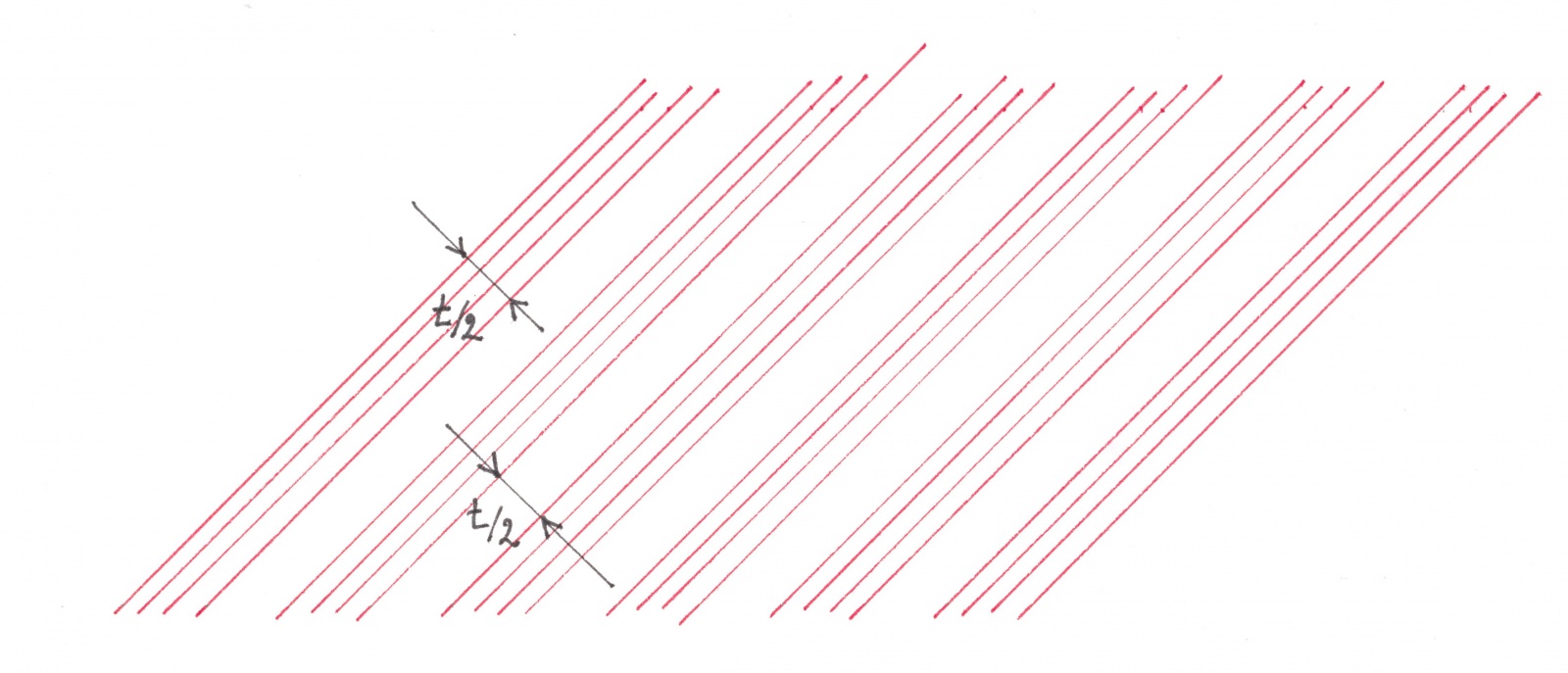
Рис. 16a
Также, в схеме обязательно присутствует хотя бы один горизонтальный поток, движущийся влево. Его красные теневые полосы изображены на рисунке 16b.
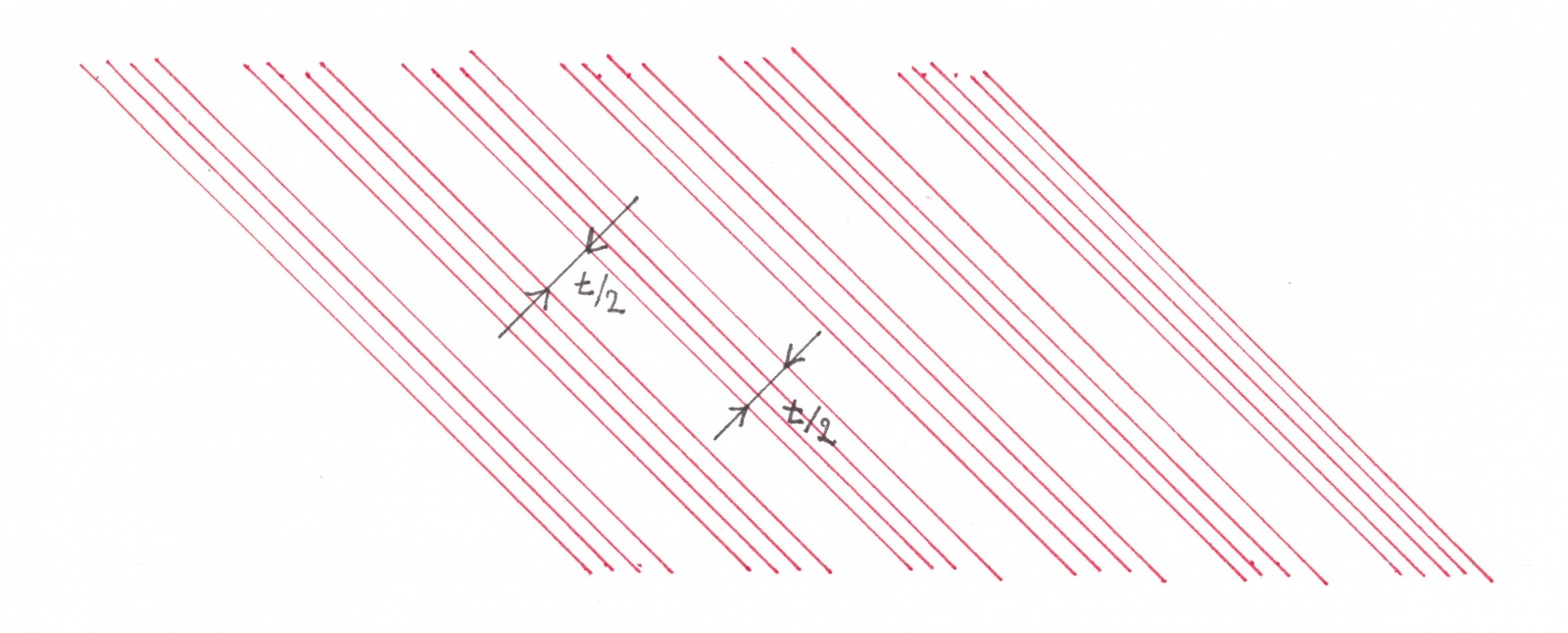
Рис. 16b
Заведомо невозможно быть уверенным, что линейчатый узор красных теневых полос от единственного взятого наугад потока, движущегося вправо, совпадет с узором всех красных правых глобальных теневых полос, ровно как нельзя быть уверенным, что линейчатый узор красных теневых полос от единственного взятого наугад потока, движущегося влево, совпадет с узором всех красных левых глобальных теневых полос. Но давайте посмотрим на клетчатый узор (рисунок 16c), который образуют вместе красные теневые полосы этих двух, выбранных наугад, потоков (рисунок 16c).
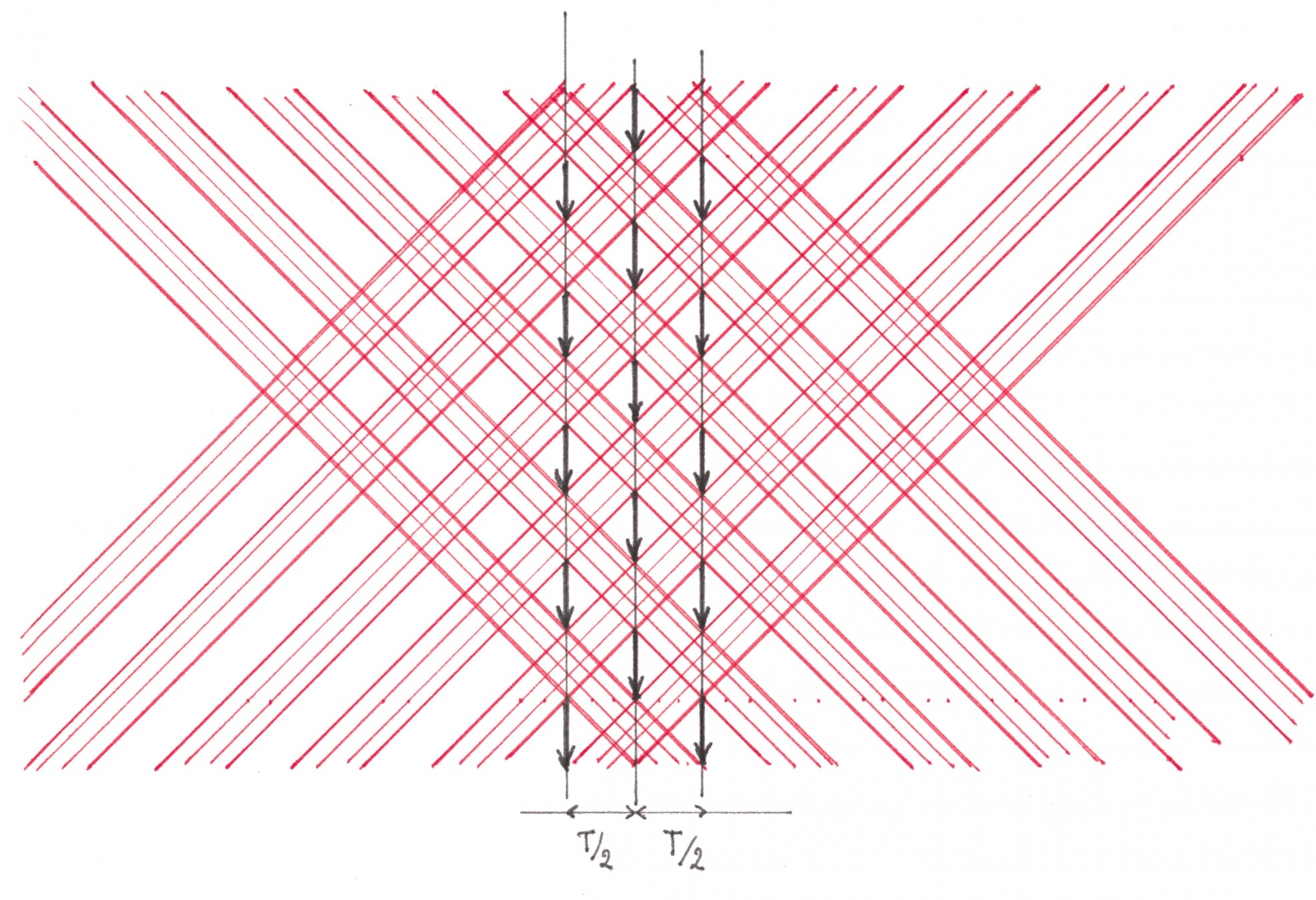
Рис. 16c
Этот узор оказывается составлен из равновеликих квадратов с величиной диагонали T/2, поэтому 50-ти процентная эффективность может быть достигнута каким-либо потоком, направленным вниз, лишь при условии, что отведенная под него дорога проходит точно через вертикальные диагонали бело-белых клеток узора. Рассматриваемый клетчатый узор, будучи порожденным черными зонами только части от всех потоков схемы движения, обязан тем самым содержаться внутри ассоциированного с этой схемой глобального красно-красного узора. Но, как мы можем заметить, еще раз взглянув на рисунок 16, добавь к изображенному на нем клетчатому узору хоть одну красную полосу, или на толику расширь уже имеющиеся — и ни один направленный вниз поток уже не сможет обладать эффективностью в 50%.
Последнее наблюдение позволяет сделать несколько выводов о свойствах любых предельно эффективных схемах движения:
- Линейчатый узор (как красного, так и синего цвета) любого горизонтального потока совпадает с глобальным.
- Цветовые клетки всех четырех ассоциированных со схемой движения клетчатых узоров являются равновеликими квадратами с длинной диагонали T/2.
- Расстояние между ближайшими друг к другу потоками, движущимися в одном направлении, кратно T/2.
- Схема движения, приведенная на рисунке 5, обладает наименьшим по отношению к периоду зеленых волн размером кварталов среди всех двунаправленных схем предельной эффективности.
Некоторые цепочки проделанных нами выводов можно обратить, получив тем самым:
Лемма о порождении предельно эффективных схем движения
Возьмем два произвольно расположенных друг относительно друга клетчатых узора с диагональным расположением полос, первый из которых — красно-красный, а второй — сине-синий. Пусть цветовые клетки обоих узоров являются равновеликими квадратами с длиной диагонали равной T/2. Нанесем на плоскость любую сеть из горизонтальных и вертикальных потоков, лишь бы их положения удовлетворяли следующим требованиям:
- Каждый поток, направленный вниз, должен проходить через вертикальные диагонали бело-белых клеток красно-красного узора;
- Каждый поток, направленный вверх, должен проходить через вертикальные диагонали бело-белых клеток сине-синего узора;
- Каждый поток, направленный вправо, должен проходить через горизонтальные диагонали красно-синих клеток красно-синего производного узора;
- Каждый поток, направленный влево, должен проходить через горизонтальные диагонали сине-красных клеток сине-красного производного узора.
Если по этим узорам для нанесенной на плоскость сети дорог канонически построить размещение зеленых волн, то в результате будет получена предельно эффективных схема движения.(Докажите самостоятельно). Тот факт, что описанным способом можно получить каждую предельно эффективную схему движения немедленно следует из свойства инволюнтности процедуры канонического построения.
Итак, одна предельно эффективная схема движения с двусторонними улицами у нас уже есть, но размер кварталов, которые она предполагает, — целых 500 метров. Предельно эффективные схемы движения наиболее привлекательны с точки зрения затрат на строительство дорог и экономии городского пространства, однако для них действует ограничение на расстояние меду потоками, направленными в одну сторону: оно не может быть меньше полупериода зеленой волны, или все тех же 500-та метров.
Возможно ли сделать кварталы меньше?
Единственная логическая лазейка, которая нам остается, — отказаться от двустороннего движения и попытаться чередовать потоки с противоположными направлениями: в случае успеха протяженность кварталов составит только четверть периода зеленой волны, или вполне приемлемые 250 метров.
Наудачу, такая схема движения действительно существует и, по всей видимости, именно она является самой перспективной для применения на практике. Одно из мгновенных положений ее потоков изображено на рисунке 17.
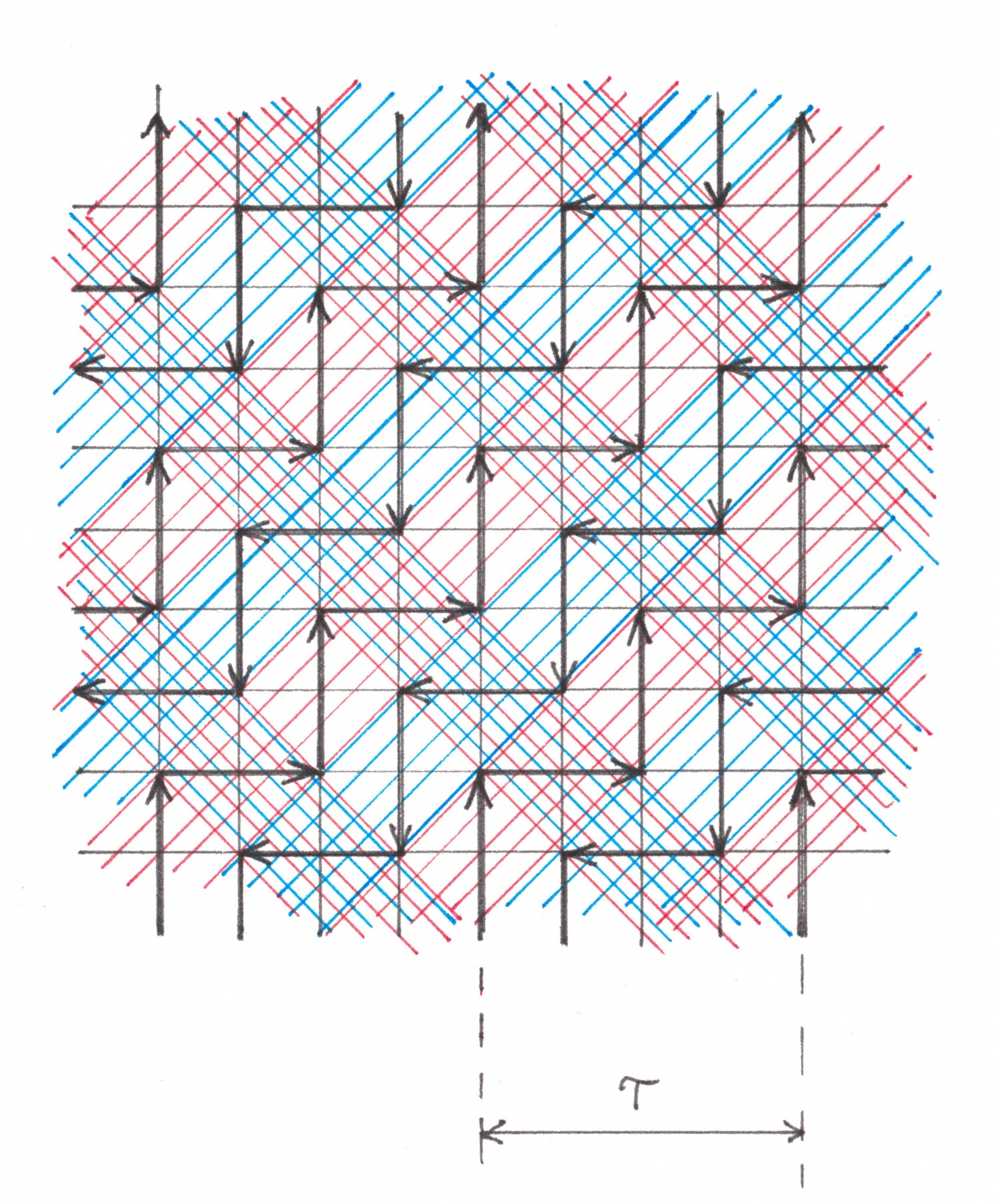
Рис. 17
Как должен измениться облик современных городов
Давайте оценим, сколько еще потребуется построить дорог, чтобы каждый сотрудник мог добираться до места соей работы на личном авто. Возьмем для начала сравнительно небольшой город со 150-ю тысячами населения при стандартной плотности в 10 тысяч человек на квадратный километр. Вся территория такого городка легко уместится внутри матрицы 16×16 кварталов (квадрата 4 × 4 километра), а путешествие между двумя его самыми удаленными друг от друга точками по свободным дорогам не займет больше десяти минут.
Сделаем упрощающее допущение, что во всех кварталах сосредоточено одинаковое количество как рабочих мест, так и постоянно там живущих горожан, при этом никакой статистической связи между адресом дома и работы не наблюдается. В таком случае, почти все жители во время утренней миграции покинут пределы своих кварталов, а из каждого квартала в каждый будет следовать примерно одинаковое количество людей. Мы будем предполагать, что для организации уличного движения используется транспортная схема рисунка 17 с ограничением, разрешающим выезд из кварталов только на горизонтальные дороги, а заезд — только со стороны вертикальных.
Попробуем найти, каким будет максимальный поток автомобилей на отдельно взятой улице в утренний час пик.
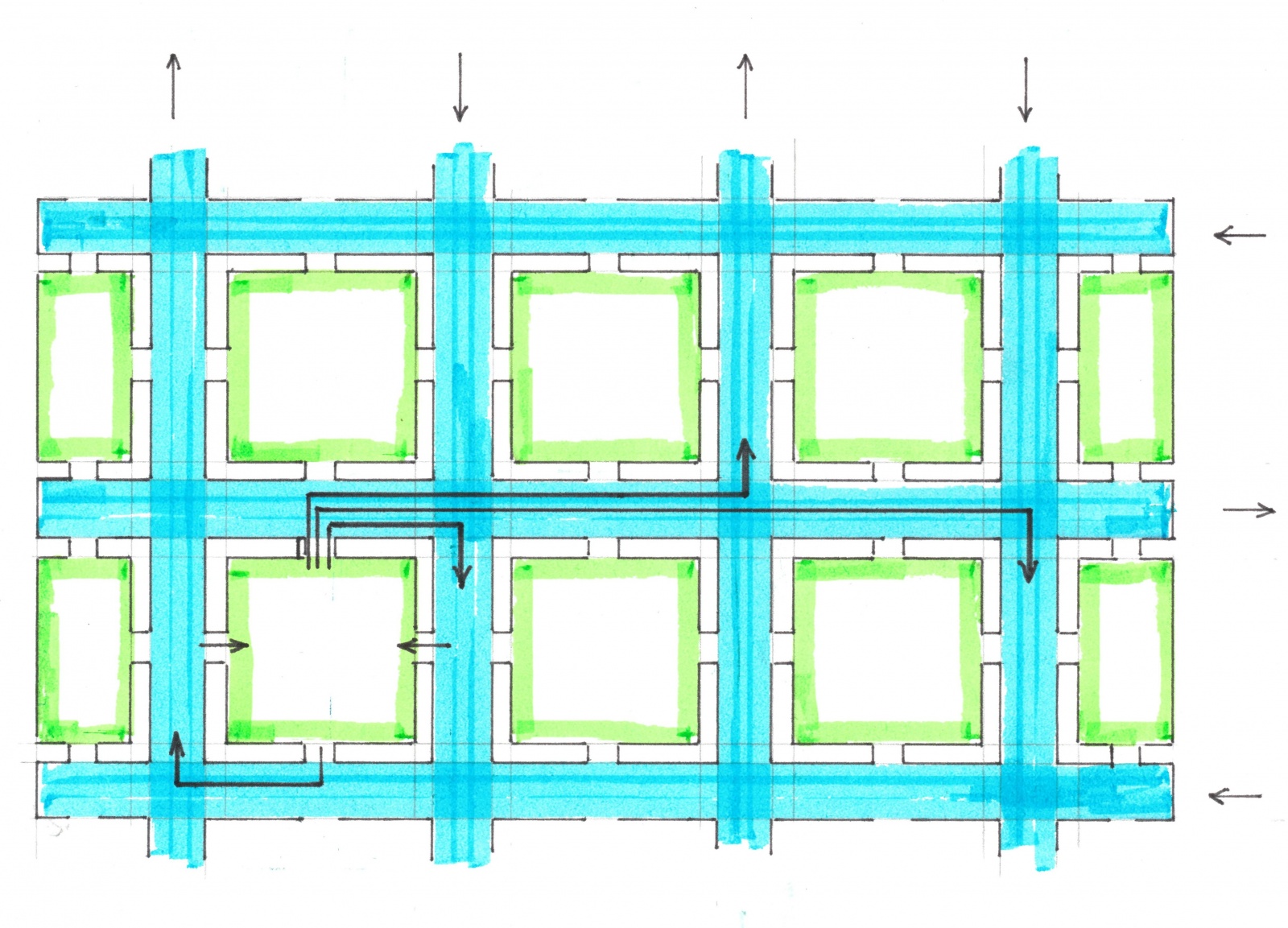
Рис. 18
На рисунке 18 изображен фрагмент карты с аналогичной схемой движения, но меньших размеров. На этой карте отмечены все маршруты, которые, стартовав внутри выбранного квартала, расходятся затем по разным вертикальным улицам. На каждый квартал приходится одинаковое число таких маршрутов (по числу вертикальных улиц), а на каждый маршрут — одинаковое число автомобилей, которые будут по нему следовать.
Если поперек горизонтальной дороги с движением вправо провести черту, по правую сторону
от которой останется X кварталов, а полевую Y вертикальных улиц, то эту черту пересечет X × Y маршрутов. Максимальное значение их числа будет наблюдаться ровно посередине дороги и в случае, когда улица простирается в длину на 16 кварталов, оно окажется равен 108-и (16 кварталов слева × 8 вертикальных дорог справа). В каждом квартале проживает 1/4 × 1/4 × 10 000 = 625 человек, по статистике примерно 320 из них работают, следовательно, на каждый из 16 ведущих от квартала маршрутов приходится по 20 человек, таким образом, середину каждой горизонтальной улицы пересекают 108 × 20 = 2200 автомобилей.
Представим, что в нашем гипотетическом городе действует консервативный уклад, когда рабочий день у большинства жителей начинается в 9 утра. Все служащие отправятся на работу примерно в одно и тоже время, но под влиянием возраста, особенностей характера и случайных обстоятельств, период начала утренней миграции скорее всего растянется примерно на четверть часа.
Итак, 2200 автомобилей должны проехать мимо вас по улице за четверть часа, сколько полос дороги для этого нужно построить?
По одной полосе при скорости движения — 1 километр в минуту, дистанции — 30 метров и эффективности использования дороги в режиме зеленых волн — 50% за четверть часа мимо успевает проехать всего 250 автомобилей, а для 2200 автомобилей потребуется целых 10 полос, иными словами, «Ленинский проспект» на каждой улице среднего провинциального городка.
Раз, проделанные расчеты показывают, что от консервативных взглядов стоит избавляться, сделаем так, чтобы рабочий день начинаться у разных людей в разное время. В условиях нового ритма жизни число полос можно уменьшить до вполне приемлемого значения. Например, приход на работу сотрудников, распределенный между четырьмя моментами: 9:00, 9:15, 9:30 и 9:59, обойдется возведением на каждой улице всего лишь трехполосной дороги.
К сожалению, для мегаполисов, как не размазывай начало дня по чашке кофе, количество полос все равно остается монструозным. Для построенного со всем умом 15-и миллионного города, длина улиц, а вместе с ней и число полос на дорогах вырастут примерно в 10 раз (без применения эстакад — квадратный корень из числа раз, в которое увеличилось население).
30 полос через каждые 250 метров — это, и правда, город вашей мечты?
Подводя итоги, я хотел бы поделиться своим видением ситуации:
- Автомобиль — полезное изобретение, которое при современном состоянии технологий должно быть доступно каждому гражданину в цивилизованном обществе.
- При разумном подходе совсем не сложно организовать свободное движение, хранение и пеший доступ к личным автомобилям, нисколько не нарушая уют городов разумной величины. Для городов с населением меньше 1 миллиона этого можно добиться без возведения эстакад.
- Проблема автомобильного движения внутри мегаполисов не может быть решена только в рамках дорог со светофорным регулированием и остается пока открытой.
Пришло время заняться вопросом о зависимости между густотой расположения дорог и возможностью их эффективного использования.
Меры густоты и эффективности
Перво-наперво избавимся от необходимости употреблять каждый раз фразу: «по отношению к величине пространственного периода зеленых волн» и договоримся, что отныне период всех этих волн равен единице.
Количественной мерой густоты расположения дорог внутри сети будем считать длину самого протяженного квартала в городе. Эту величину договоримся называть мажоратной мелкостью сети. Мажоратная мелкость корректно определена для всех моделей городов (даже с бесконечным числом кварталов) конечной протяженности.
Для конкретно выбранного размещения зеленых волн, значения эффективности использования дорог его потоками может оказаться разной для разных потоков. Нижнюю грань множества этих значений разумно назвать миноратной эффективностью выбранного размещения. Для размещений зеленых волн на сетях с конечным числом дорог значение миноратной эффективности совпадает со значением эффективности наиболее неэффективно используемой дороги.
Приведу несколько связанных с этим понятие утверждений, которые читатель, надеюсь, без труда сможет доказать самостоятельно.
- В любом размещении зеленых волн можно таким образом урезать черные зоны всех потоков, что после все они станут одной длины, а миноратная эффективность размещения не изменится.
- Возьмем для какого-нибудь размещения ассоциированные с ним клетчатые узоры и применим к ним каноническую процедуру Леммы о порождении. Миноратная эффективность полученного в итоге размещения будет не меньше, чем у исходного.
- Пусть миноратная эффективность некоторого размещения равна D. Удалим из ассоциированных с ним красно-красного и сине-синего клетчатых узоров сначала все цветные полосы, ширина которых меньше D/√2, заменив их на белый фон. Затем удалим все белые полосы, с шириной меньше D/√2, закрасив их в каждом случае основным цветом узора, после чего используем два, уже видоизмененных, узора в качестве изначальных для канонического процесса Леммы о порождении — значение миноратной эффективности полученного в итоге размещения окажется большим или равным D.
Давайте возьмем все возможные размещения зеленых волн (с единичным периодом) на какой-нибудь конкретно выбранной сети. Верхнюю грань множества миноратных эффективностей этих размещений назовем миноратной эффективностью самой сети.
Иными словами, если E — миноратная эффективность дорожной сети, то существуют размещения зеленых волн на этой сети со значениями миноратной эффективности сколь угодно близкими к E.
Фактом куда более нетривиальный является то, что, по крайней мере, для одного размещения близость превращается в точное равенство. План доказательства этого утверждения приведен в конце статьи.
Универсальный объект в мире дорожных сетей
Представьте, что вдоль каждой горизонтальной и вдоль каждой вертикальной прямой разрешено движение в обоих направлениях. Вряд ли когда-нибудь хоть один город в мире сможет похвастаться такой дорожной сетью, но как математический объект она вполне реальна и, к тому же, обладает полезным свойством Универсальности: содержит любую другую дорожную сеть Манхетонского типа в качестве своей подсети. Каждое размещение зеленых волн на Универсальной сети, обладающее миноратной эффективностью D, (индуцирует) порождает на каждой ее подсети размещение зеленых волн с миноратной эффективностью большей или равной D. Как следствие этого, миноратная эффективность любой дорожной сети Манхетонского типа больше или равна значения миноратной эффективности для Универсальной сети.
Главная интрига теперь заключается в вопросе: равна ли миноратная эффективность Универсальной сети нулю, а если — нет, то каковое ее истинное значение.
Оценка сверху
Миноратная эффективность любого размещения зеленых волн на Универсальной дорожной сети не превосходит 1/4.
Доказательство достаточно провести только для таких размещений, каждое из которых использует все дороги с равной эффективностью (утверждение 1 предыдущего параграфа). Произвольно выберем одно из таких размещений и обозначим его эффективность как δ (период T =1). Каждый поток этого размещения составлен из чередующихся друг с другом черных зон длины δ и белых зон длины 1 — δ. Построим красные теневые полосы для каких-нибудь двух встречных потоков выбранного размещения. Пересекаясь, эти полосы образуют клетчатый узор, фрагмент которого вы можете видеть на рисунке 18.
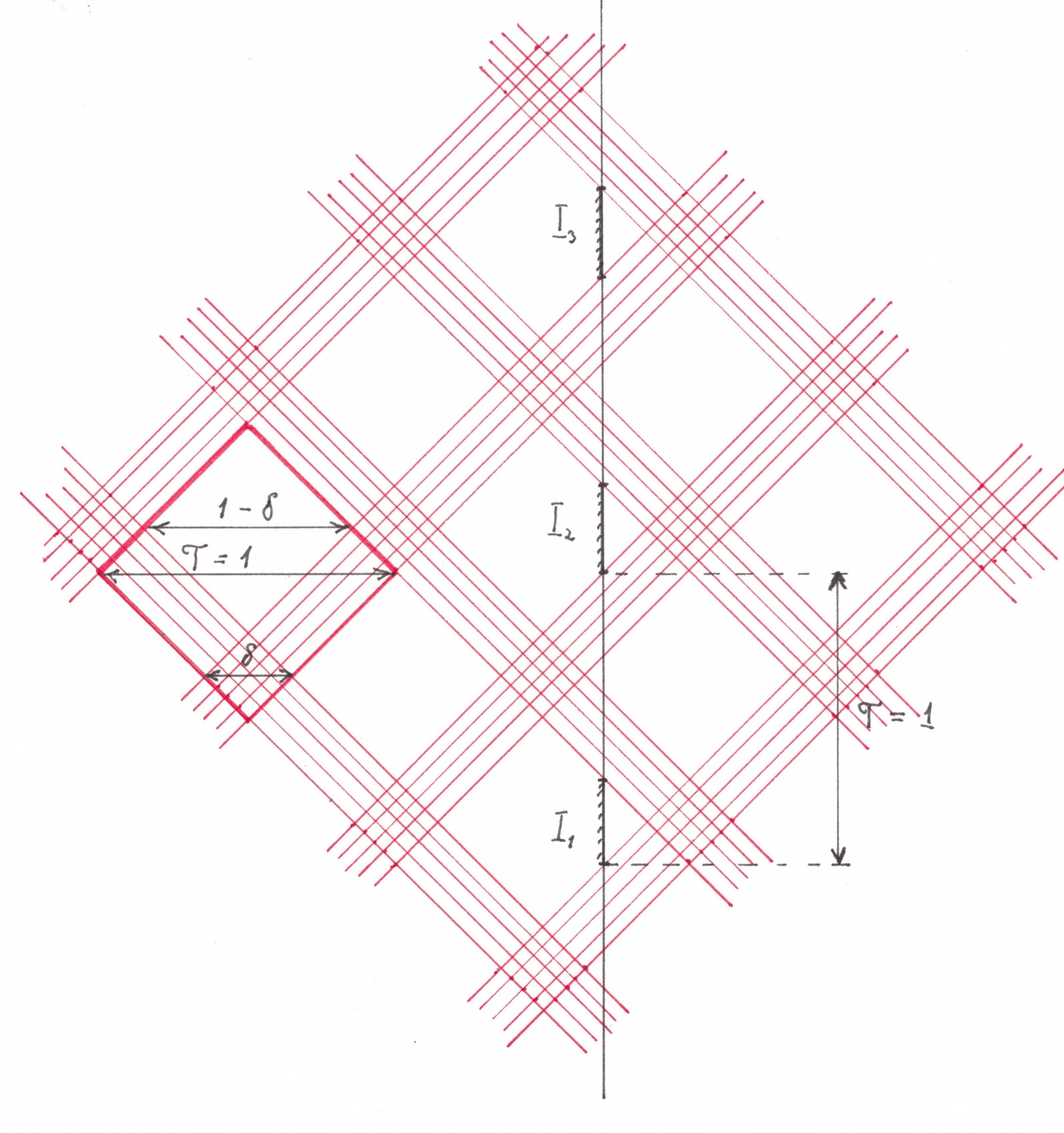
Рис. 19
Элементарная ячейка этого узора будет иметь форму квадрата с диагональю единичной длины, а его красные полосы — пересекать любую горизонтальную или вертикальную прямую по отрезку величиной δ.
Черные зоны потоков, направленных вниз, могут располагаться только внутри бело-белых клеток, поэтому у каждой вертикальной прямой должны быть области пересечения с бело-белыми клетками длины большей или равной δ. Наименее выигрышное положение, с этой точки зрения, у прямых, проходящих ровно посередине между вертикальными диагоналями белых квадратов (рисунок 20).
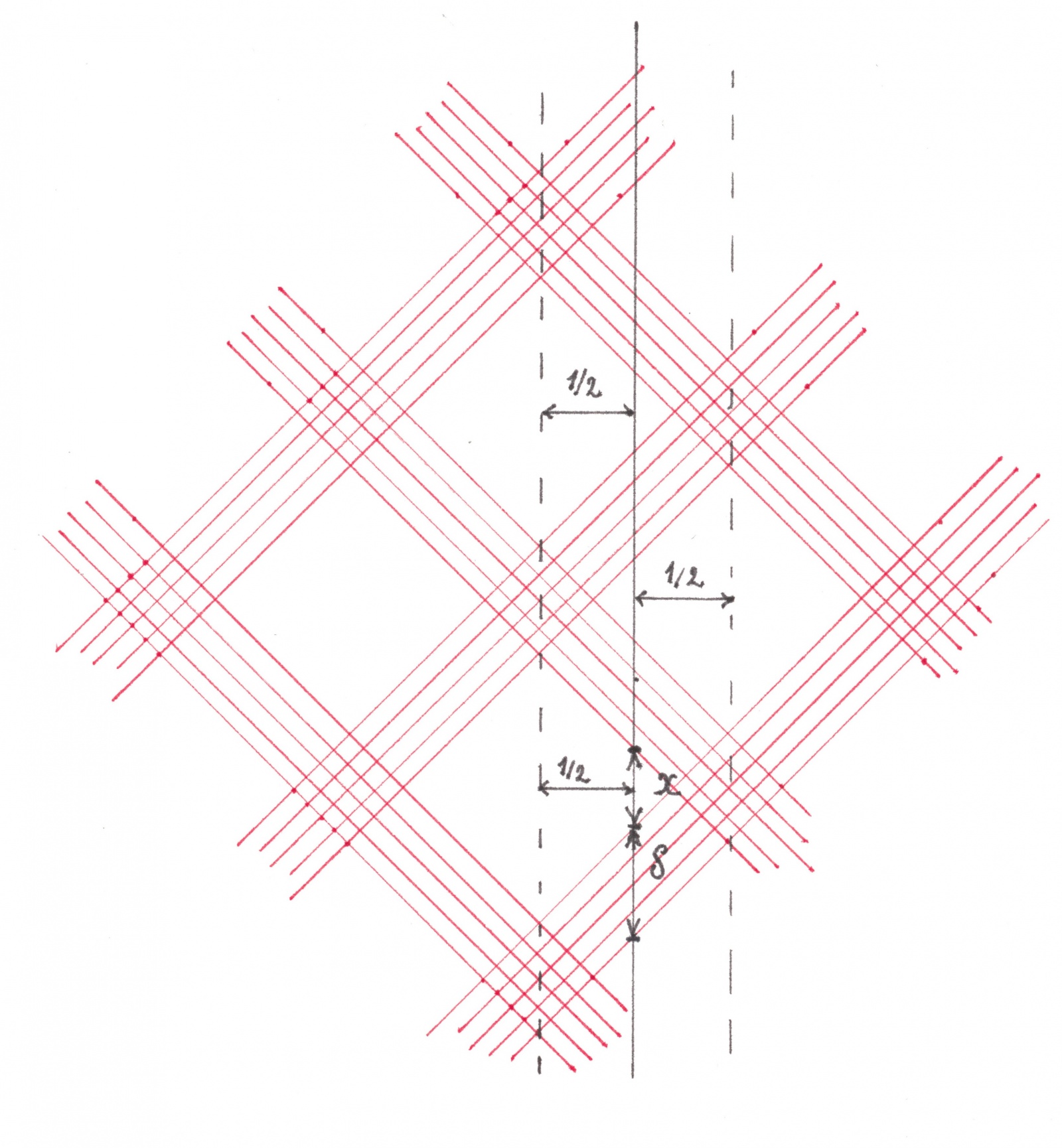
Рис. 20
Обозначая через x длины отрезков, по которым каждая из таких прямых пересекается с бело-белыми клетками и используя подобие треугольников, получаем уравнение:
x + δ = 1/2. Откуда, учитывая неравенство x ≥ δ, находим δ ≤ 1/4.
Оценка снизу
Миноратная эффективность Универсальной дорожной сети больше или равна 1/6.
Следствие:
На любой дорожной сети Манхетонского типа, какой бы плотной и непериодичной она не была, всегда найдется размещение зеленых волн с миноратной эффективностью большей или равной 1/6.
На Универсальной сети мне удалось разыскать размещение зеленых волн с миноратной эффективностью 1/6. Порождающий клетчатый узор этого размещения представлен на рисунке 21:
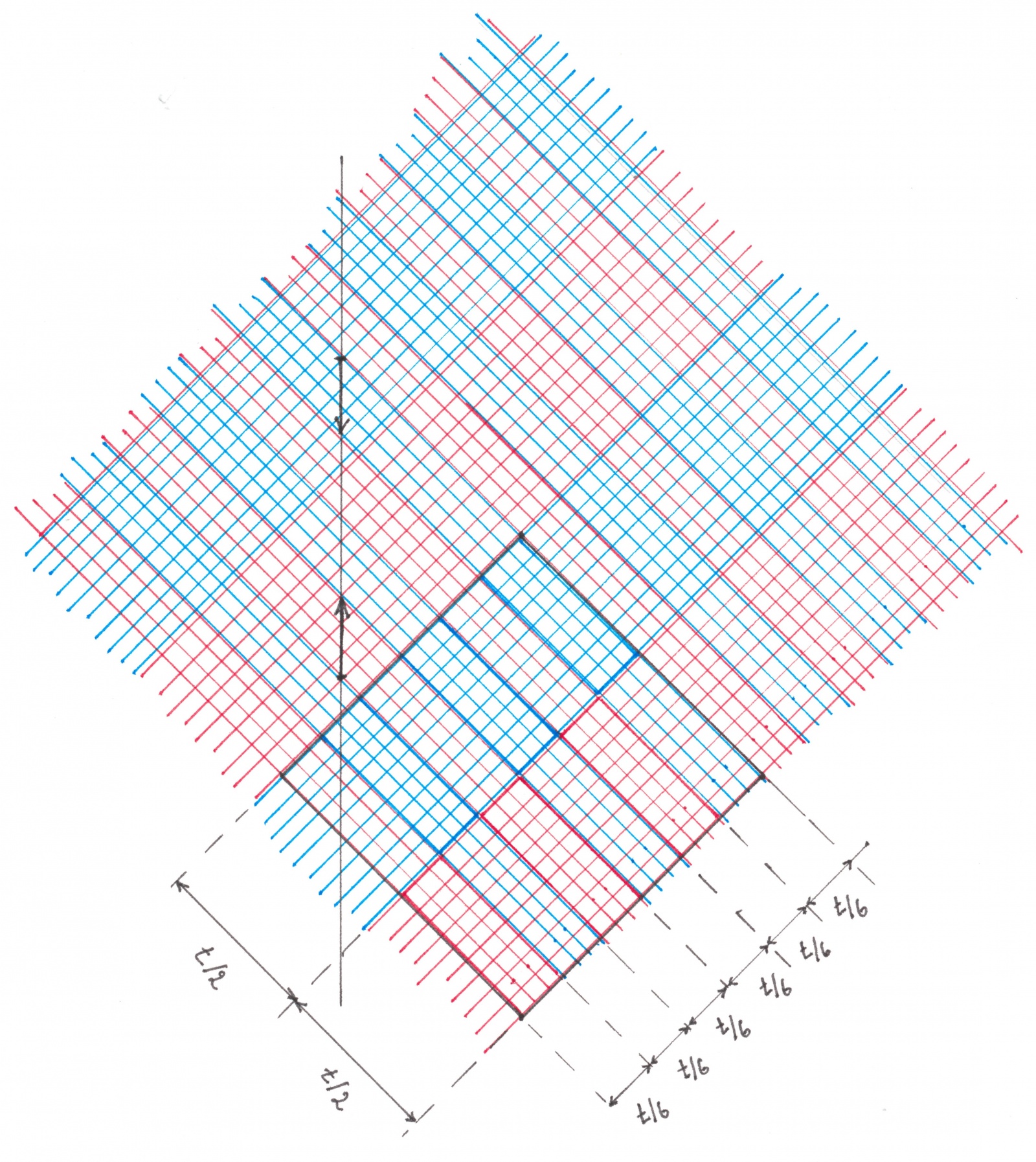
Рис. 21
Как видно из рисунка 21, любая вертикальная прямая на своем пути обязательно пересечет один из красно-красных прямоугольников по наибольшему из возможных отрезков, длина которого как раз 1/6. Вместе с периодичностью узора это служит доказательством, что эффективность всех потоков, направленных вниз равна 1/6 -ой. Для потоков других направлений эффективность также равна 1/6, что можно воспользовавшись симметрией клетчатого узора.
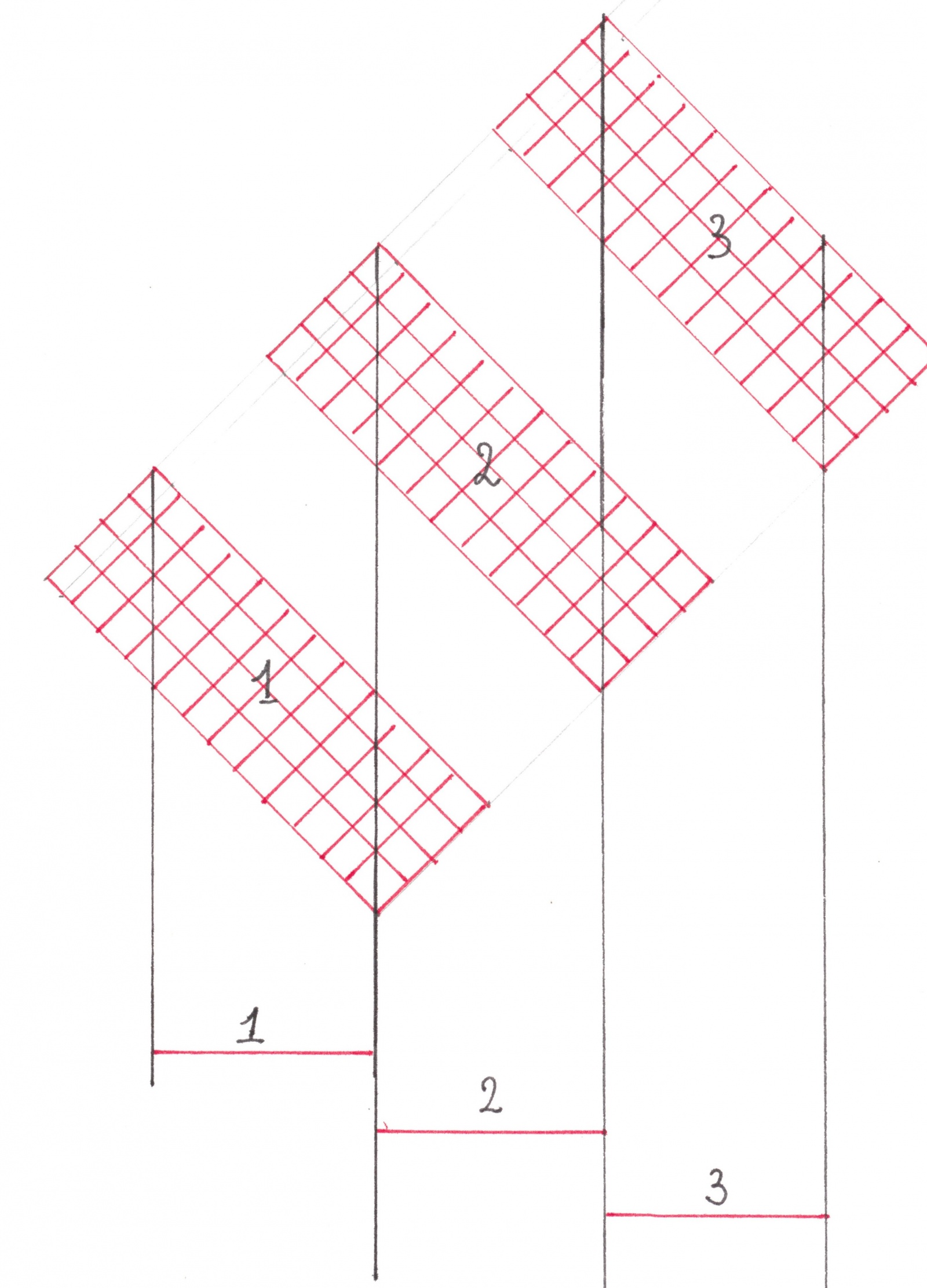
Рис. 22
Хорошая исследовательская задача:
Каково подлинное значение миноратной эффективности Универсальной сети?
На этот вопрос можно ответить с помощью линейного программирования — программа выйдет довольно заковыристая, но со скромным числом ограничений. Интересно было бы найти значение эффективности как-то изящно. Быть может одному из вас эта задача окажется по плечу.
Благодарю за внимание и желаю удачи!
Сергей Коваленко.
2019 год.
magnolia@bk.ru
Автор: Sergey_Kovalenko




