Приближалось восьмое марта, у меня была реализация автоматизированной отрисовки поверхностей сплайнами — почему бы не написать статью с цветами.
Получилось примерно так:

Под катом будет еще, берегите трафик.
Алгоритм, который делает кубические кривые, был описан ранее. Здесь попробуем применить его для получения чего-то цветочкообразного. Проблема только в том, как подобрать входные данные.
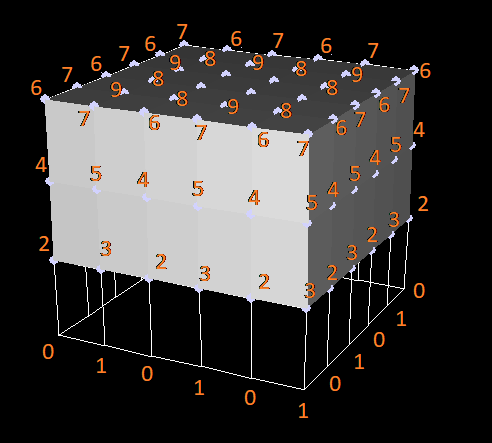
Входные даные — это набор точек с координатами в трехмерном пространстве и набор связей между ними, таких, что топологически эта конструкция должна быть эквивалентна ящичку, типа такого:

(в конце должно быть так:)

Чтобы кубические поверхности при натяжении на остов были похожи на цветок, надо расположить точки симметрично, на окружностях, описанных вокруг центра цветка. Для решения этой задачи была применена вариация «поиска в ширину».
Присвоим всем точкам веса. Сначала крайним точкам присвоим веса 0 и 1 (два одинаковых веса не должны стоять рядом). Это будут края «лепестков», 0 — дальние, 1 — ближние («лепестки» в кавычках, потому что как такового разделения на лепестки здесь нет). Взвешиваем дальше, присваивая вес n+2 невзвешенным соседям с весом n.
Взвешенный ящик:
Далее случайным образом выбираем расстояния r от центра цветка для каждой весовой категории.
Логика тут следующая: чем больше вес, тем ближе точку надо будет передвинуть к центру, причем должны выполняться неравенства:
где r — расстояние от центра цветка до точек с соответствующим весом. Четные веса отвечают за центральную часть «лепестка», нечетные — за края «лепестка».
Для того, чтобы располагать точки на окружностях (а не на сферах), нам так же придется случайным образом выбрать z-координаты таким образом, что z_n < r_n (если центр цветка в координатном нуле).

На следующем шаге нам надо узнать углы для расположения точек на окружности:
и далее координаты для i-й точки веса n, если он четный:
для нечетного:
Кроме того, важен порядок, в котором мы берем точки — они должны быть «соседями».

После всех этих манипуляций получается звездообразная конструкция, на которую можно натянуть сплайны.
(вид сверху, изометрия, сплайны)


Таких чашелистиков можно нарандомить 100500, но отбирать из них годные, составлять из нескольких цветок, подбирать цвета и параметры сердцевины лучше вручную, поэтому генерация полуавтоматическая.
(вид ПО для сборки)






Поздравляю с международным женским днем прекрасную половину хабрасообщества! Надеюсь, вам было красиво.
Автор: Rikhmayer