Любой аналитик, в начале своей работы, проходит ненавистный этап определения идентификации параметров распределения. Потом, с наработкой опыта, для него согласование полученных остаточных разбросов означает, что какой-то этап, в анализе Big Data, пройден и можно двигаться дальше. Уже нет необходимости проверять сотни моделей на соответствие различным уравнениям регрессии, искать отрезки с переходными процессами, составлять композицию моделей. Терзать себя сомнениями: «Может есть, еще какая-нибудь модель, которая больше подходит?»
Подумал: «А что, если пойти от противного. Посмотреть, что может сделать белый шум. Может ли белый шум создать, что-то, что наше внимание сопоставит со значимым объектом из нашего опыта?»
Рис. Белый шум (файл взят из сети, размер 448х235).
По этому вопросу рассуждал так:
1. Какова вероятность, что появится горизонтальные и вертикальные линии, заметной длины?
2. Если они могут появиться, то какова вероятность, что они совпадут своим началом по одной из координат и составят прямоугольную фигуру?
Дальше по тексту, объясню, как эти задачи связались с анализом Big Data.
В книге Г.Секей «Парадоксы в теории вероятностей и математической статистике» (стр.43) обнаружил ссылку на теорему Эрдёша-Реньи, которая звучит так:
При бросании монеты n раз, серия из гербов длины 
наблюдается с вероятностью, стремящейся к 1, при n стремящемся к бесконечности.
Для нашего рисунка это означает, что в каждой из 235 строк с вероятностью, стремящейся к 1, найдется:
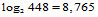
то есть отбрасываем до целого – 8-ми черных точек подряд по горизонтали.
И для всех 448 столбцов, с вероятностью, стремящейся к 1, найдется:
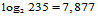
отбрасывая до целого — 7 черных точек подряд, по вертикали.
Отсюда получаем вероятность того, что в «белом шуме» будет составлен черный прямоугольник размером 8х7 пикселей, для этой картинки:
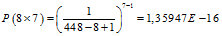
Где 1 – это первая последовательность из черных точек в строке, в любом месте двумерного пространства.
Не спорю, что вероятность очень маленькая, но не нулевая.
Двигаясь дальше, мы можем соединить, все строки в одну и получим строку, длиной 102 225 знаков. И тогда по теореме Эрдёша-Реньи, с вероятностью стремящейся к 1, существует цепочка, длиной:
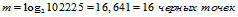
А для цепочки из 1 млн.записей:
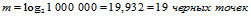
Как видим, связь теоремы Эрдёша-Реньи, с Big Data, обозначилась однозначно.
Примечание. Далее буду излагать свой собственный анализ выявленного. Так как в той форме, этой теоремы и ее доказательства, которая представлена в книге Г.Секея, мне обнаружить не удалось.
Получаем, что теорема Эрдёша-Реньи, может использоваться тестом, по определению однородности данных.
Она применима к распределениям, имеющим центральный момент первого порядка (МХ).
Она может применяться только к одноканальным последовательным случайным процессам.
Как ее применять
Любое распределение, с матожиданием, мы можем представить, как отклонение от центра: влево-вправо, вверх-вниз. То есть выпадение: орла-решки.
Соответственно, по этой теореме, должен обнаруживаться интервал, в котором последовательные значения, в количестве 
находятся выше или ниже МХ (Y(xi)).
Примечание. В этом аспекте хотелось увидеть доказательство этой теоремы, чтобы понять существует только один такой подряд (только выше или ниже) или два (выше и ниже). По моим размышлениям, симметричность этих явлений должно порождать два подряда и, с другой стороны, анализируя доказательство похожего процесса, этих математиков, относящееся к графам, то предположил, что они строили доказательство на определении максимума. Что допускает и существование доказательства на минимизации целевой функции. Возникали вопросы о том, как теорема Эрдёша-Реньи выглядит для несимметричных вероятностей, для вариантов более 2.
Практическим следствием обнаружения, только одного, такого последовательного подряда, в исследуемой базе, дает нам возможность допускать, что все представленные данные однородны.
Второе. Если обрабатывая данные, по теореме Эрдёша-Реньи, мы обнаружили, что существует ряд больший по количеству значений, чем он должен быть, то вероятна ситуация, представленная на рисунке.
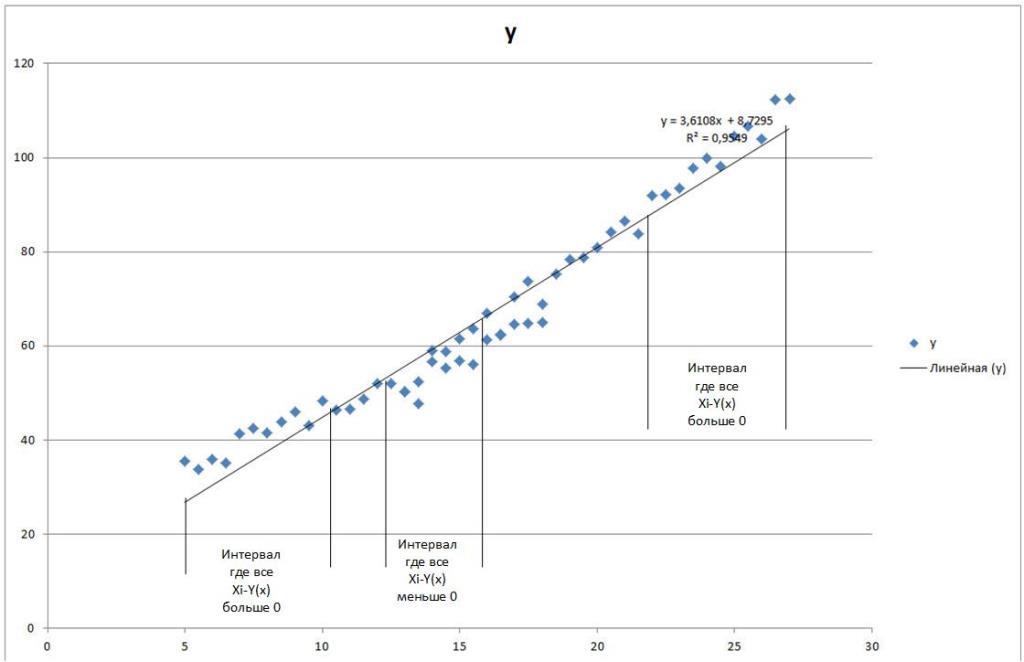
Представленный на рисунке ряд, составлен как композиция двух функций, для целей примера.
Третье заключение. Если обрабатывая данные (1 млн.записей), по теореме Эрдёша-Реньи, не было обнаружено ни одного ряда длиной 19 номеров, но обнаружилось, допустим, три последовательности с 17 номерами. То можно предположить, что общие данные состоят из композиции трех функций, и по месту этих рядов, определить интервалы в которых, возможно, происходят переходные процессы.
Когда работал над этим материалом, сверсталось наблюдение о следующем. Все, разработанные методы анализа данных, сделаны для технологий, когда, по небольшим естественным наблюдениям, необходимо определить параметры гораздо большей совокупности, по 100 наблюдениям, определить свойства генеральной совокупности объемом 1 млн. или больше. А для современных задач, когда необходимо провести декомпозицию огромной БД, разработанные статистикой инструменты очень трудоемки.
Автор: Sistemaalex
