Линейная регрессия и методы её восстановления

2019-09-09 в 7:15, admin, рубрики: distributed computing, machine learning, math, математика, машинное обучение, распределенные системы

Источник: xkcd

Линейная регрессия является одним из базовых алгоритмов для многих областей, связанных с анализом данных. Причина этому очевидна. Это очень простой и понятный алгоритм, что способствует его широкому применению уже многие десятки, если не сотни, лет. Идея заключается в том, что мы предполагаем линейную зависимость одной переменной от набора других переменных, а потом пытаемся эту зависимость восстановить.

Но в этой статье речь пойдет не про применение линейной регрессии для решения практических задач. Здесь будут рассмотрены интересные особенности реализации распределенных алгоритмов её восстановления, с которыми мы столкнулись при написании модуля машинного обучения в Apache Ignite. Немного базовой математики, основ машинного обучения и распределенных вычислений помогут разобраться, как восстанавливать линейную регрессию, даже если данные распределены между тысячами узлов.

О чём речь?

Перед нами стоит задача восстановления линейной зависимости. В качестве входных данных дается множество векторов предположительно независимых переменных, каждому из которых ставится в соответствие некоторое значение зависимой переменной. Эти данные можно представить в виде двух матриц:

$begin{pmatrix} a_{11} & a_{12} & a_{13} & ... & a_{1n} \ a_{21} & a_{22} & a_{23} & ... & a_{2n} \ ... \ a_{m1} & a_{m2} & a_{m3} & ... & a_{mn} \ end{pmatrix} begin{pmatrix} b_{1} \ b_{2} \ ... \ b_{m} \ end{pmatrix}$

Теперь, раз уж предполагается зависимость, да к тому же еще и линейная, запишем наше предположение в виде произведения матриц (для упрощения записи здесь и далее предполагается, что свободный член уравнения скрывается за $x_n$ , а последний столбец матрицы $A$ содержит единицы):

$begin{pmatrix} a_{11} & a_{12} & a_{13} & ... & a_{1n} \ a_{21} & a_{22} & a_{23} & ... & a_{2n} \ ... \ a_{m1} & a_{m2} & a_{m3} & ... & a_{mn} \ end{pmatrix} times begin{pmatrix} x_{1} \ x_{2} \ ... \ x_{n} \ end{pmatrix}=begin{pmatrix} b_{1} \ b_{2} \ ... \ b_{m} \ end{pmatrix}$

Очень похоже на систему линейных уравнений, не так ли? Похоже, но решений у такой системы уравнений скорее всего не будет. Причиной тому является шум, который присутствует практически в любых реальных данных. Так же причиной может быть отсутствие линейной зависимости как таковой, с которой можно пытаться бороться введением дополнительных переменных, нелинейно зависящих от исходных. Рассмотрим следующий пример:

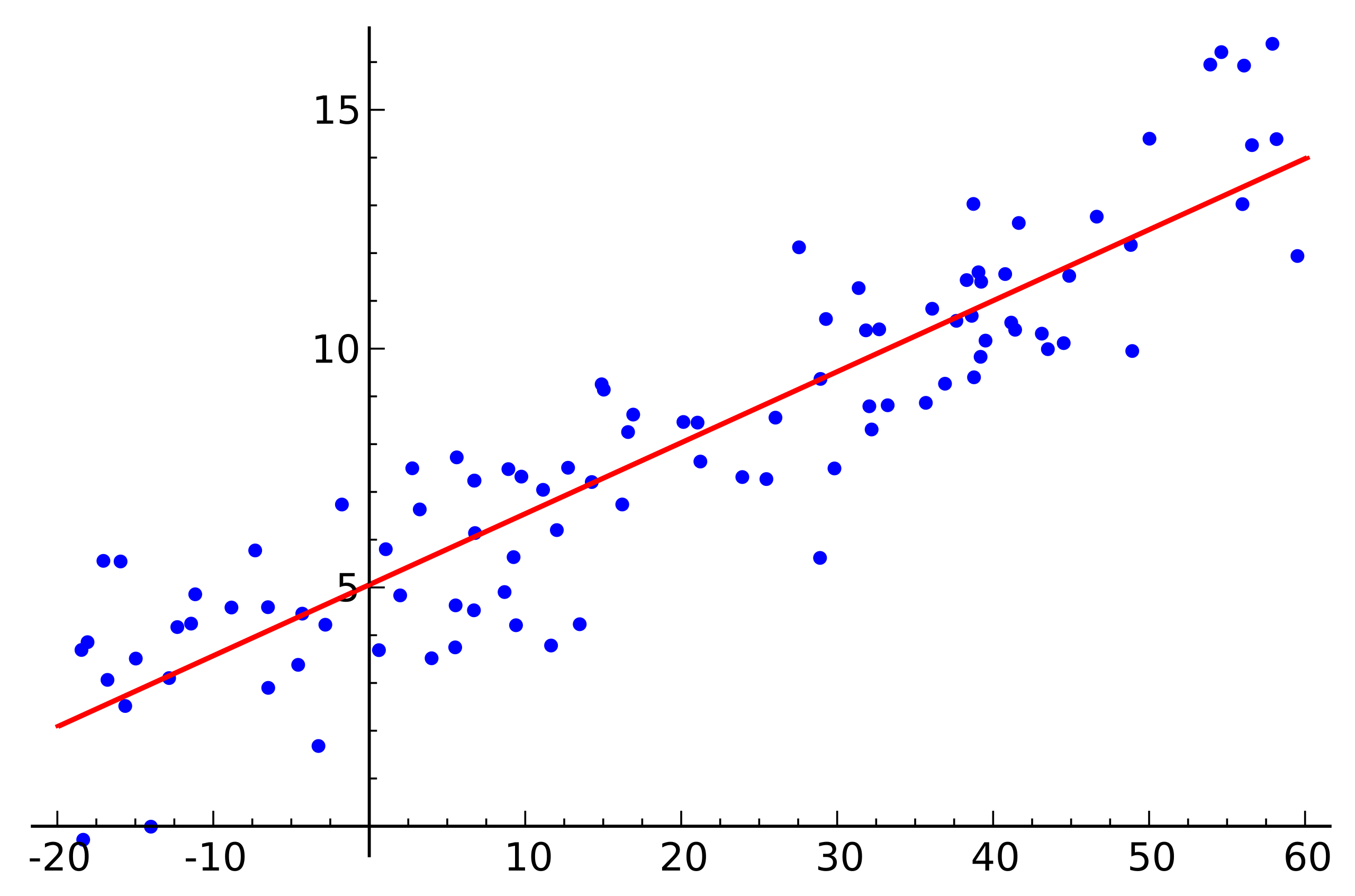
Источник: Wikipedia

Это простой пример линейной регрессии, который демонстрирует зависимость одной переменной (по оси $y$ ) от другой переменной (по оси $x$ ). Чтобы соответствующая данному примеру система линейных уравнений имела решение, все точки должны лежать точно на одной прямой. Но это не так. А не лежат они на одной прямой именно из-за шума (или из-за того что предположение о наличии линейной зависимости было ошибочным). Таким образом, чтобы восстановить линейную зависимость по реальным данным обычно требуется ввести еще одно предположение: входные данные содержат шум и этот шум имеет нормальное распределение. Можно делать предположения и о других типах распределения шума, но в подавляющем большинстве случаев рассматривают именно нормальное распределение, о котором далее и пойдет речь.

Метод максимального правдоподобия

Итак, мы предположили наличие случайного нормально распределенного шума. Как же быть в такой ситуации? На этот случай в математике существует и широко используется метод максимального правдоподобия. Если кратко, его суть заключается в выборе функции правдоподобия и последующей её максимизации.

Возвращаемся к восстановлению линейной зависимости по данным с нормальным шумом. Заметим, что предполагаемая линейная зависимость является математическим ожиданием $mu$ имеющегося нормального распределения. В то же время, вероятность того, что $mu$ принимает то или иное значение, при условии наличия наблюдаемых $x$ , выглядит следующим образом:

$P(mu mid X, sigma^2)=prod_{x in X}{frac{1}{sigmasqrt{2pi}}; e^{ -frac{(x-mu)^2}{2sigma^2} }}$

Подставим теперь вместо $mu$ и $X$ нужные нам переменные:

$P(x mid A, B, sigma^2)=prod_{i in [1, m]}{frac{1}{sigmasqrt{2pi}}; e^{ -frac{(b-ax)^2}{2sigma^2} }}, a_i in A, b_i in B$

Осталось только найти вектор $x$ , при котором эта вероятность максимальна. Чтобы максимизировать такую функцию удобно сначала её прологарифмировать (логарифм функции будет достигать максимума в той же точке, что и сама функция):

$f(x)=ln(prod_{i in [1, m]}{frac{1}{sigmasqrt{2pi}}; e^{ -frac{(b-ax)^2}{2sigma^2} }})=sum_{i in [1, m]}lnfrac{1}{sigmasqrt{2pi}}; - sum_{i in [1, m]}frac{(b-ax)^2}{2sigma^2}$

Что, в свою очередь, сводится к минимизации следующей функции:

$f(x)=sum_{i in [1, m]} (b-ax)^2$

Кстати, это называется методом наименьших квадратов. Зачастую все приведенные выше рассуждения опускаются и просто используется этот метод.

QR разложение

Минимум приведенной выше функции можно найти, если найти точку в которой градиент этой функции равен нулю. А градиент будет записан следующим образом:

$nabla f(x)=sum_{i in [1, m]}2a_i(a_ix - b_i)=0$

QR разложение является матричным методом решения задачи минимизации используемом в методе наименьших квадратов. В связи с этим перепишем уравнение в матричной форме:

$A^T A x=A^Tb$

Итак, мы раскладываем матрицу $A$ на матрицы $Q$ и $R$ и выполняем ряд преобразований (сам алгоритм QR разложения здесь рассматриваться не будет, только его использование применительно к поставленной задаче):

$begin{align} & (QR)^T (QR) x=(QR)^Tb; \ & R^T Q^T Q R x=R^T Q^T b; \ end{align}$

Матрица $Q$ является ортогональной. Это позволяет нам избавиться от произведения $Q Q^T$ :

$begin{align} & R^T R x=R^T Q^T b; \ & (R^T)^{-1} R^T R x=(R^T)^{-1} R^T Q^T b; \ & R x=Q^T b. end{align}$

А если заменить $Q^T b$ на $z$ , то получится $R x=z$ . Учитывая, что $R$ является верхней треугольной матрицей, выглядит это следующим образом:

$begin{pmatrix} r_{11} & r_{12} & r_{13} & r_{14} & ... & r_{1n} \ 0 & r_{22} & r_{23} & r_{24} & ... & r_{2n} \ 0 & 0 & r_{33} & r_{34} & ... & r_{3n} \ 0 & 0 & 0 & r_{44} & ... & r_{4n} \ ... \ 0 & 0 & 0 & 0 & ... & r_{nn} \ end{pmatrix} times begin{pmatrix} x_1 \ x_2 \ x_3 \ x_4 \ ... \ x_n end{pmatrix}=begin{pmatrix} z_1 \ z_2 \ z_3 \ z_4 \ ... \ z_n end{pmatrix}$

Это можно решать методом подстановки. Элемент $x_n$ находится как $z_n / r_{nn}$ , предыдущий элемент $x_{n-1}$ находится как $(z_{n-1} - r_{n-1,n}x_n) / r_{n-1,n-1}$ и так далее.

Здесь стоит отметить, что сложность получившегося алгоритма за счет использования QR разложения равна $O(2mn^2)$ . При этом, несмотря на то, что операция умножения матриц хорошо распараллеливается, написать эффективную распределенную версию этого алгоритма не представляется возможным.

Градиентный спуск

Говоря о минимизации некоторой функции, всегда стоит вспоминать метод (стохастического) градиентного спуска. Это простой и эффективный метод минимизации, основанный на итеративном вычислении градиента функции в точке и последующем её смещении в сторону, противоположную градиенту. Каждый такой шаг приближает решение к минимуму. Градиент при этом выглядит все так же:

$nabla f(x)=sum_{i in [1, m]}2a_i(a_ix - b_i)$

Ещё этот метод хорошо распараллеливается и распределяется за счет линейных свойств оператора градиента. Заметим, что в приведенной выше формуле под знаком суммы находятся независимые слагаемые. Другими словами, мы можем посчитать градиент независимо для всех индексов $i$ с первого до $k$ , параллельно с этим посчитать градиент для индексов с $k+1$ до $m$ . Затем сложить получившиеся градиенты. Результатом сложения будет таким же, как если бы мы посчитали сразу градиент для индексов с первого до $m$ . Таким образом, если данные распределены между несколькими частями данных, градиент может быть вычислен независимо на каждой части, а затем результаты этих вычислений могут быть просуммированы для получения окончательного результата:

$nabla f(x)=sum_{i in P_1}2a_i(a_ix - b_i) + sum_{i in P_2}2a_i(a_ix - b_i) + ... + sum_{i in P_k}2a_i(a_ix - b_i)$

С точки зрения реализации, это укладывается в парадигму MapReduce. На каждом шаге градиентного спуска на каждый узел данных отправляется задание на вычисление градиента, затем вычисленные градиенты собираются вместе, и результат их суммирования используется для улучшения результата.

Несмотря на простоту реализации и возможность выполнения в парадигме MapReduce градиентный спуск обладает и своими недостатками. В частности, количество шагов, необходимое для достижения сходимости, существенно больше в сравнении с другими более специализированными методами.

LSQR

LSQR — еще один метод решения поставленной задачи, который подходит как для восстановления линейной регрессии, так и для решения систем линейных уравнений. Его главная особенность заключается в том, что он совмещает в себе преимущества матричных методов и итеративного подхода. Реализации этого метода можно найти как в библиотеки SciPy, так и в MATLAB. Описание данного метода приводиться здесь не будет (его можно найти в статье LSQR: An algorithm for sparse linear equations and sparse least squares). Вместо этого будет продемонстрирован подход, позволяющий адаптировать LSQR к выполнению в распределенной среде.

В основе метода LSQR лежит процедура бидиагонализации. Это итеративная процедура, каждая итерация которой состоит из следующих шагов:

Но если исходить из того, что матрица $A$ горизонтально партиционирована, то каждую итерацию можно представить в виде двух шагов MapReduce. Таким образом удается минимизировать пересылками данных в ходе каждой из итераций (только вектора длиной равной количеству неизвестных):

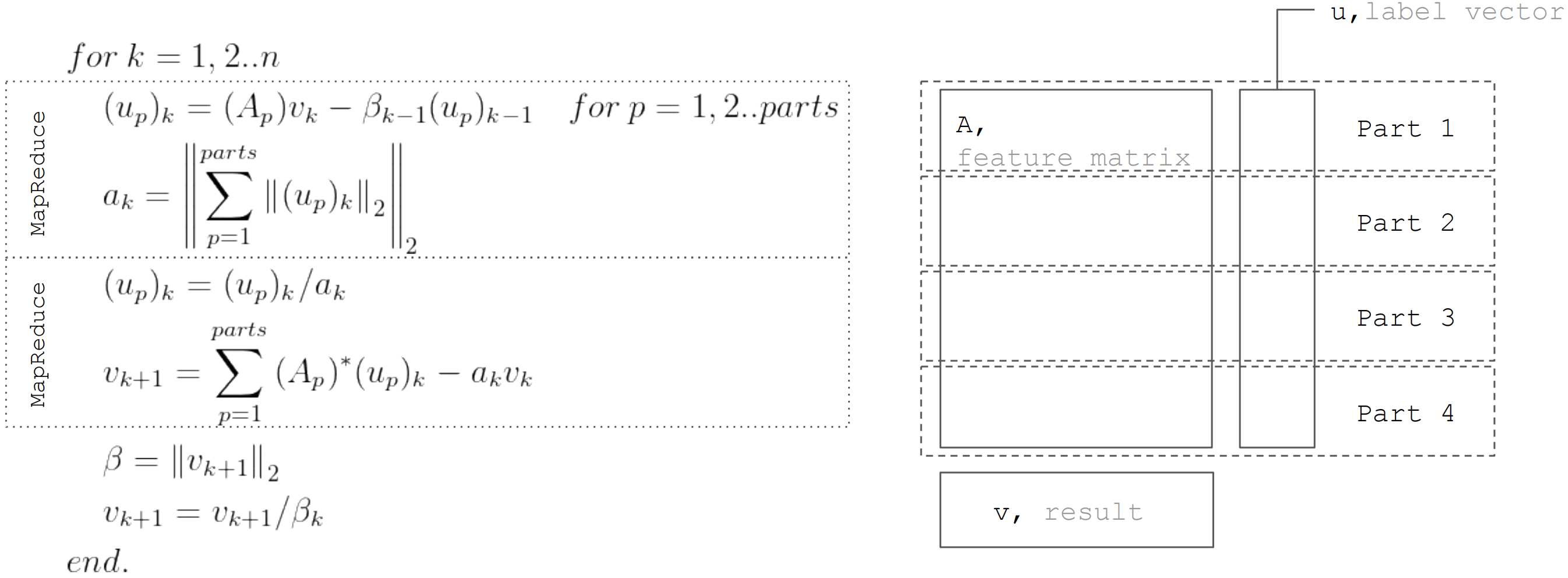
Именно этот подход используется при реализации линейной регрессии в Apache Ignite ML.

Заключение

Существует много алгоритмов восстановления линейной регрессии, но не все из них могут применяться в любых условиях. Так QR разложение отлично подходит для точного решения на небольших массивах данных. Градиентный спуск просто реализуется и позволяет быстро найти приближенное решение. А LSQR сочетает в себе лучшие свойства предыдущих двух алгоритмов, так как он может быть распределен, быстрее сходится в сравнении с градиентным спуском, а так же позволяет раннюю остановку алгоритма в отличие от QR-разложения для поиска приближенного решения.

Автор: Anton Dmitriev

Источник

Информация

Обсуждаемое

Рекомендуем