Главная

Оцениваем опционы на Clojure методом Монте-Карло

2020-04-03 в 10:46, admin, рубрики: clojure, jvm, Блог компании Exness, опционы, Программирование, финансы, финансы в IT, ФП, функциональное программирование

Привет! Меня зовут Рома, я работаю iOS-разработчиком в Exness. А кроме того, пишу на Clojure и инвестирую.

Сегодня я расскажу о том, как оценивать опционы. Это вводная статья и заработать миллион, используя предложенный способ, вряд ли получится. Тем не менее, это хорошая основа для понимания более сложных методов оценки.

Оцениваем опционы на Clojure методом Монте-Карло - 1

Clojure

Почему Clojure?

В основе языка лежат преобразования неизменяемых данных, а стандартная библиотека содержит сотни функций для этого, что очень помогает при решении финансовых задач.

Кроме того, Clojure работает на JVM, а значит, доступны все финансовые библиотеки, написанные на Java.

Наконец, REPL. Если вы не работали с Clojure, представьте Jupyter Notebook на стероидах. Можно писать код в полноценной IDE и при этом постоянно взаимодействовать с запущенной программой.

Опционы

Я не буду углубляться в детали того, что такое опцион, и как он работает – на Хабре много статей на эту тему. Ограничимся функцией, которая определяет результат колл-опциона на дату его экспирации:

(defn call-option-value [security-price strike-price]
    (Math/max (- security-price strike-price) 0))

;; examples
(call-option-value 360.0 280.0) 
=> 80.0
(call-option-value 10.0 280.0) 
=> 0.0

Понятно, что будущую цену базового инструмента мы не знаем. Тем не менее, нужно как-то определить стоимость опциона сегодня.

Большинство методов оценки строятся на простом принципе: мы пытаемся понять, какие результаты возможны, усредняем их, а затем дисконтируем результат.

Гипотетический пайплайн на Clojure выглядит так:

(-> (get-possible-outcomes) mean present-value))

Аналогично работает и метод Монте-Карло, только возможные результаты мы получаем путем проведения множества симуляций:

(-> (repeatedly n simulate-outcome) mean present-value)))

Монте-Карло

Напишем функцию, которая будет моделировать движение цены до момента экспирации опциона. Мы будем использовать вариант геометрического броуновского движения.

Для начала, шаг цены:

(defn gbm-step [price dt rate volatility]
  (let [drift (* price rate dt)
        shock (* price volatility (Math/sqrt dt) (gaussian))
        change (+ drift shock)]
    (+ price change)))

;; next day price    
(gbm-step 1200 1/365 0.01 0.15)
=> 1207.554940519062

Как видно из сигнатуры, кроме стартовой цены, нам также нужны безрисковая ставка и волатильность в годовом выражении. Мы будем использовать ставку по трежерам и историческую волатильность.

Так как цена на завтра зависит только от сегодняшней цены, можем воспользоваться функцией iterate для получения всех будущих цен.

Смоделируем движение цены акции Apple ($257) на следующие 100 дней:

(take 100 (iterate #(gbm-step % 1/365 0.01 0.15) 257))
=>
(257
 258.6727911540819
 256.91541924148663
 252.98034966342195
 251.1008036685261
 ...

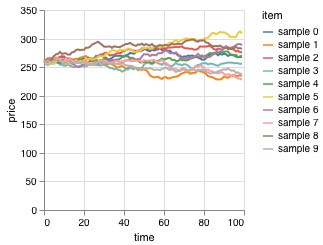
Запустим симуляцию 10 раз и посмотрим, что получилось:

Оцениваем опционы на Clojure методом Монте-Карло - 2

После того, как мы научились прогнозировать цену базового инструмента на дату экспирации, используем ее для получения финансового результата по опциону:

(defn simulate-outcome [price strike rate volatility expiration]
  (let [steps 100
        dt (/ expiration steps)
        prices (iterate #(gbm-step % dt rate volatility) price)
        price-at-expiration (last (take steps prices))]
    (call-option-value price-at-expiration strike)))

;; simulate 5 outcomes for one option
(repeatedly 5 #(simulate-outcome 1924 1925 0.01 0.45 0.5))
=> (0.0 730.6715047778875 329.1915857113486 0.0 0.0)

Экспирация здесь измеряется в долях года. То есть, для опциона, исполняющегося через год, она равна 1.

Наконец, основной интерфейс:

(defn evaluate-call-option [& {:keys [security-price strike-price risk-free-rate volatility expiration]}]
  (let [expiration (year-fraction-until expiration)
        simulate-fn (partial simulate-outcome security-price strike-price risk-free-rate volatility expiration)
        n 1000]
    (-> (repeatedly n simulate-fn) mean (present-value risk-free-rate expiration))))

;; example    
(evaluate-call-option
  :security-price 1924
  :strike-price 1925
  :risk-free-rate 0.01
  :volatility 0.45
  :expiration (LocalDate/of 2020 4 17))
=> 74.66533445636996

Попробуем оценить опционы на Amazon со страйком от 2100 до 2140 и экспирацией 17 апреля:

(for [strike (range 2100 2150 10)]
  (evaluate-call-option
     :security-price 1987
     :strike-price strike
     :risk-free-rate 0.01
     :volatility 0.35
     :expiration (LocalDate/of 2020 4 17)))
=> (23.9 21.1 16.4 15.5 15.3)

А вот рыночные цены на момент написания:

=> (22.9 20.6 18.35 16.4 14.6 13.6)

Несмотря на простоту метода, нам удалось достаточно близко к ним подойти.

Заключение

На этом все. Код проекта доступен по ссылке. В следующей статье я расскажу о том, как сделать кросс-платформенный десктопный интерфейс с помощью библиотеки cljfx и использовать его для отображения портфеля опционов.