Во второй части будут рассмотрены арифметическое кодирование и преобразование Барроуза-Уилера (последнее часто незаслуженно забывают во многих статьях). Я не буду рассматривать семейство алгоритмов LZ, так как про них на хабре уже были неплохие статьи.
Итак, начнем с арифметического кодирования — на мой взгляд, одного из самых изящных (с точки зрения идеи) методов сжатия.
Введение
В первой части мы рассмотрели кодирование Хаффмана. Несмотря на то, что это прекрасный, проверенный временем алгоритм, он (как и любые другие) не лишен своих недостатков. Проиллюстрируем слабое место алгоритма Хаффмана на примере. При кодировании методом Хаффмана, относительные частоты появления символов в потоке приближаются к частотам, кратным степеням двойки. По теореме Шеннона, напомню, наилучшее сжатие будет достигнуто, если каждый символ частотой f ьудет закодирован с помощью -log2f бит. Построим небольшой график (заранее приношу извинения, так как в построении красивых графиков я не силен).
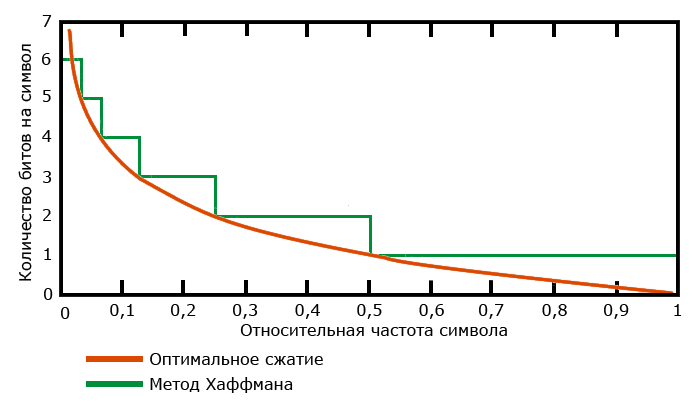
Как можно заметить, в случаях, когда относительные частоты не являются степенями двойки, алгоритм явно теряет в эффективности. Это легко проверить на простом примере потока из двух символов a и b с частотами 253/256 и 3/256 соответственно. В этом случае в идеале нам понадобится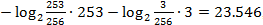 
, то есть 24 бита. В то же время, метод Хаффмана закодирует эти символы кодами 0 и 1 соответственно, и сообщение займет 256 бит, что, конечно, меньше 256 байт исходного сообщения (напомню, мы предполагаем, что изначально каждый символ имеет размер в байт), но все же в 10 раз меньше оптимума.
Итак, перейдем к рассмотрению арифметического кодирования, которое позволит нам получить лучший результат.
Арифметическое кодирование
Как и метод Хаффмана, арифметическое кодирование является методом энтропийного сжатия. Кодируемые данные представляются в виде дроби, которая подбирается так, чтобы текст можно было представить наиболее компактно. Что же это значит на самом деле?
Рассмотрим построение дроби на интервале [0,1) (такой интервал выбран для удобства подсчета), и на примере входных данных в виде слова «короб». Нашей задачей будет разбить исходный интервал на субинтервалы с длинами, равными вероятностям появления символов.
Составим таблицу вероятностей для нашего входного текста:
| Символ | Частота | Вероятность | Диапазон |
| О | 2 | 0.4 | [0.0, 0.4) |
| К | 1 | 0.2 | [0.4, 0.6) |
| Р | 1 | 0.2 | [0.6, 0.8) |
| Б | 1 | 0.2 | [0.8, 1.0) |
Здесь под «Частотой» подразумевается количество вхождений символа во входном потоке.
Будем считать, что данные величины известны как при кодировании, так и при декодировании. При кодировании первого символа последовательности (в нашем случае — "Короб"), используется весь диапазон от 0 до 1. Этот диапазон необходимо разбить на отрезки в соответствии с таблицей.
В качестве рабочего интервала берется интервал, соответствующий текущему кодируемому символу. Длина этого интервала пропорциональна частоте появления символа в потоке.
После нахождения интервала для текущего символа, этот интервал расширяется, и в свою очередь разбивается в соответствии с частотами, так же как и предыдущие (то есть, для нашего примера, на шаге 2 мы должны разбить интервал от 0.4 до 0.6 на субинтервалы так же, как сделали это на первом шаге). Процесс продолжается до тех пор, пока не будет закодирован последний символ потока.
Иными словами, i-му символу будет ставиться в соответствие интервал
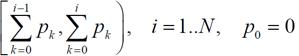
где N — количество символов алфавита, pi — вероятность i-го символа.
В нашем случае это выглядит так
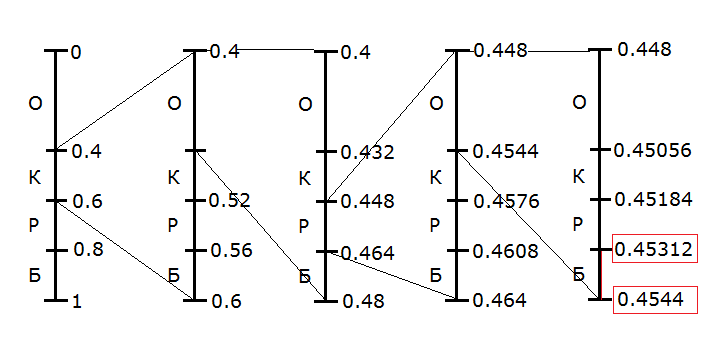
Итак, мы последовательно сужали интервал для каждого символа входного потока, пока не получили на последнем символе интервал от 0.45312 до 0.4544. Именно его мы и будем использовать при кодировании.
Теперь нам нужно взять любое число, лежащее в этом интервале. Пусть это будет 0,454. Как ни удивительно (а для меня, когда я только изучал этот метод, это было весьма удивительно), этого числа, в совокупности со значениями частот символов, достаточно для полного восстановления исходного сообщения.
Однако для успешной реализации, дробь должна быть представлена в двоичной форме. В связи с особенностью представления дробей в двоичной форме (напомню, что некоторые дроби, имеющие конечное число разрядов в десятичной системе имеют бесконечное число разрядов в двоичной), кодирование обычно производится на основании верхней и нижней границы целевого диапазона.
Как же происходит декодирование? Декодирование происходит аналогичным образом (не в обратном порядке, а именно аналогичным образом).
Мы начинаем с интервала от 0 до 1, разбитого в соответствии с частотами символов. Мы проверяем, в какой из интервалов попадает наше число (0,454). Символ, соответствующий этому интервалу и будет первым символом последовательности. Далее, мы расширяем этот интервал на всю шкалу, и повторяем процедуру.
Для нашего случая процесс будет выглядеть так:
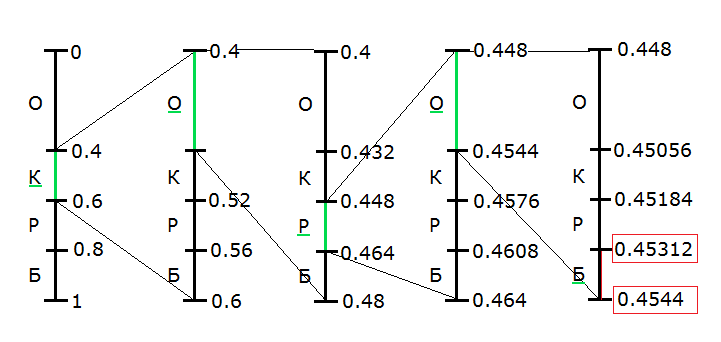
Конечно, ничто не мешает нам продолжить уменьшать интервал и увеличивать точность, получая все новые и новые «символы». Поэтому, при кодировании таким способом нужно либо заранее знать количество символов исходного сообщения, либо ограничить сообщение уникальным символом, чтобы можно было точно определить его конец.
При реализации алгоритма стоит учитывать некоторые факторы. Во-первых, алгоритм в виде представленном выше может кодировать только короткие цепочки из-за ограничения разрядности. Чтобы избежать этого ограничения, реальные алгоритмы работают с целыми числами и оперируют с дробями, числитель и знаменатель которых являются целым числом.
Для оценки степени сжатия арифметического кодирования нам нужно найти минимальное число N, такое, что внутри рабочего интервала при сжатии последнего символа можно заведомо найти число, в двоичном представлении которого после N знаков идут только нули. Для этого длина интервала должна быть не меньше, чем 1/2N. При этом известно, что длина интервала будет равна произведению вероятностей всех символов.
Рассмотрем предложенную в начале статьи последовательность символов a и b с вероятностями 253/256 и 3/256. Длина последнего рабочего интервала для цепочки из 256 символов будет равна
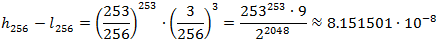
В таком случае, искомое N будет равно 24 (23 дает слишком большой интервал, а 25 не будет являться минимальным), то есть мы потратим на кодирование всего 24 бита, против 256 бит метода Хаффмана.
Преобразование Барроуза — Уилера
Итак, мы выясняли, что методы сжатия показывают разную эффективность на разных наборах данных. Исходя из этого, возникает вполне логичный вопрос: если на определенных данных алгоритмы сжатия работают лучше, то нельзя ли перед сжатием производить с данными некоторые операции для улучшения их «качества»?
Да, это возможно. Для иллюстрации, рассмотрим преобразование Барроуза Уилера, которое превращает блок данных со сложными зависимостями в блок, структура которого легче моделируется. Еслественно, это преобразование также полностью обратимо. Авторами метода являются Девид Уилер (David Wheeler) и Майк Барроуз (Michael Burrows, если верить вики, сейчас он работает в Google).
Итак, алгоритм Барроуза-Уилера (в дальнейшем для краткости я буду называть его BTW — Burrows-Wheeler Transform) преобразовывает входной блок в более удобный для сжатия вид. Однако, как показывает практика, полученный в результате преобразования блок обычные методы сжимают не так успешно, как специально для этого разработанные, поэтому для практического применения нельзя рассматривать алгоритм BWT отдельно от соответствующих методов кодирования данных, но поскольку наша цель — изучить принцип его работы, то ничего страшного в этом нет.
В оригинальной статье, вышедшей в 1994 году, авторами была предложена реализация кодирования на трех алгоритмах:
- Собственно, BWT
- Преобразование Move-to-Front, известное в русскоязычной литературе как перемещение стопки книг
- Статистический кодер сжатия полученных на первых двух этапах данных.
Правда, второй шаг может быть заменен на другой аналогичный алгоритм, или вовсе исключен за счет усложнения фазы кодирования. Важно понимать, что BWT никак не влияет на размер данных, он всего лишь меняет расположение блоков.
Алгоритм преобразования
BWT является блочным алгоритмом, то есть он оперирует блоками данных, и заранее знает о составе элементов блока определенного размера. Это делает затруднительным использование BWT в тех случаях, когда необходимо посимвольное сжатие, или сжатие «на лету». В принципе, такая реализация возможна, но алгоритм получится… не очень быстрым.
Принцип преобразования крайне прост. Рассмотрим его на классическом «книжном» примере — слове «абракадабра», которое прекрасно подходит нам по нескольким критериям: в нем много повторяющихся символов, и эти символы распределены по слову достаточно равномерно.
Первым шагом преобразования будет составление списка циклических перестановок исходных данных. Иными словами, мы берем исходные данные, и перемещаем последний символ на первое место (или наоборот). Мы проводим эту операцию до тех пор, пока вновь не получим исходную строку. Все полученные таким образом строки и будут являться всеми циклическими перестановками. В нашем случае это выглядит примерно так:
Абракадабра
Бракадабраа
Ракадабрааб
Акадабраабр
Кадабраабра
Адабраабрак
Дабраабрака
Абраабракад
Браабракада
Раабракадар
Аабракадабр
Мы будем рассматривать это как матрицу символов, где каждая ячейка — это один символ, соответственно, строка соответствует слову целиком. Мы помечаем исходную строку, и сортируем матрицу.
Сортировка производится сначала по первому символу, затем, для тех строк, где первый символ совпадает — по второму, и так далее. После такой сортировки наша матрица примет такой вид:
Аабракадабр
Абраабракад
Абракадабра – исходная строка
Адабраабрак
Акадабраабр
Браабракада
Бракадабраа
Дабраабрака
Кадабраабра
Раабракадаб
Ракадабрааб
В общем-то на этом преобразование почти закончено: все что осталось сделать — это записать последний столбец, не забыв при этом запомнить номер исходной строки. Сделав это, мы получим:
«р>>д<<акраааабб»
или, по-другому,
«рдакраааабб»,2
Как видим, распределение символов стало значительно лучше: теперь 4 из 5 символов «а» стоят рядом, как и оба символа «б».
Обратимость
Как я уже упоминал, преобразование полностью обратимо. Это и понятно, ведь иначе в нем не было бы никакого смысла. Так как же восстановить первоначальный вид сообщения?
Сперва нам необходимо отсортировать наши символы по порядку. Это даст нам строку «аааааббдкрр». Поскольку наша матрица циклических перестановок была отсортирована по порядку, то эта последовательность букв — ни что иное, как первый столбец нашей матрицы циклических перестановок. Кроме этого, нам известен и последний столбец (собственно, сам результат преобразования). Итак, на данном этапе мы можем восстановить матрицу до примерно такого состояния:
| а | ... | р |
| а | ... | д |
| а | ... | а |
| а | ... | к |
| а | ... | р |
| б | ... | а |
| б | ... | а |
| д | ... | а |
| к | ... | а |
| р | ... | б |
| р | ... | б |
Поскольку матрица была получена циклическим сдвигом, символы последнего и первого столбца образуют пары. Сортируя эти пары по возрастанию, мы получим уже первые два столбца. Затем, эти два столбца и последний образуют уже тройки символов, и так далее.
В конце концов мы полностью восстановим матрицу, а поскольку мы знаем номер строки, в которой содержатся исходные данные, то мы легко можем получить их первоначальный вид.
Иными словами, восстановление проводится следующим образом:
- Присоединить символы последнего столбца слева к символам первого
- Отсортировать все столбцы кроме последнего
Эти два шага нужно повторять до тех пор, пока матрица не будет полностью заполнена.
Для нашего примера первые четыре шага восстановления будут выглядеть так:
аа -> ааб -> аабр -> аабра ->...
аб -> абр -> абра -> абраа ->...
аб -> абр -> абра -> абрак ->...
ад -> ада -> адаб -> адабр ->...
ак -> ака -> акад -> акада ->...
бр -> бра -> браа -> брааб ->...
бр -> бра -> брак -> брака ->...
да -> даб -> дабр -> дабра ->...
ка -> кад -> када -> кадаб ->...
ра -> раа -> рааб -> раабр ->...
ра -> рак -> рака -> ракад ->...
Затраты ресурсов при работе
После того, как мы доказали обратимость данных, докажем то, что для осуществления алгоритма не нужно хранить в памяти всю матрицу. Действительно – если бы мы полностью хранили матрицу соответствующую, например, блоку размером в 1 мегабайт, то нам потребовалось бы колоссальное количество памяти – ведь матрица является квадратной. Естественно, такой вариант недопустим.
Для обратного преобразования нам дополнительно к собственно данным необходим вектор обратного преобразования – массив чисел, размер которого равен числу символов в блоке. Таким образом, затраты памяти при линейном преобразовании растут линейно с размером блока.
Во время обратного преобразования для получения очередного столбца матрицы совершались одни и те же действия. А именно, новая строка получалась путем соединения символа последнего столбца старой строки и известных символов этой же строки. Разумеется, после сортировки новая строка перемещалась на другую позицию в матрице. Важно, что при добавлении любого столбца перемещения строк на новую позицию должны быть одинаковы. Чтобы получить вектор обратного преобразования, нужно определить порядок получения символов первого столбца из символов последнего, то есть отсортировать матрицу по номерам новых строк
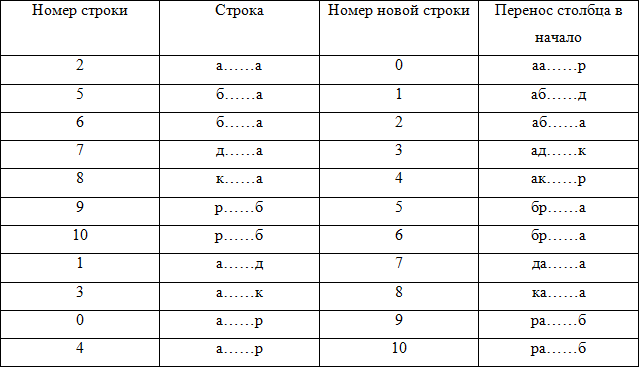
Вектор преобразования формируется из значений номеров строк: {2,5,6,7,8,9,10,1,3,0,4}.
Теперь можно легко получить исходную строку. Возьмем элемент вектора обратного преобразования, который соответствует номеру исходной строки в матрице: T[2]=6. Иначе говоря, в качестве первого символа исходной строки необходимо взять шестой символ строки «рдакраааабб» — символ «а».
После этого мы смотрим, какой символ переместил найденный символ «а» на вторую позицию среди одинаковых с ним. Для этого мы берем номер из вектора преобразования строки, из которой был взят символ «а»: это номер 6.
Затем смотрим строку, имеющую номер 6 и выбираем оттуда последний символ – это символ «б». Продолжая эту процедуру для оставшихся символов, мы легко восстановим исходную строку.
Перемещение стопки книг
Перемещение стопки книг — промежуточный алгоритм, который авторы рекомендуют использовать после BWT и перед непосредственным кодированием. Алгоритм работает следующим образом.
Рассмотрим строку «рдакраааабб», полученную нами по BWT в предыдущей части. В данном случае, наш алфавит состоит из 5 символов. Упорядочив их, получим
M={а, б, д, к, р}.
Итак, используем на нашей строке алгоритм перемещения стопки книг. Первый символ строки («р») стоит в алфавите на 4 месте. Это число (4) мы записываем в выходной блок. Затем мы помещаем только что использованный символ на первое место, и повторяем процесс со вторым символом, затем с третьим и так далее. Процесс обработки будет выглядеть так (под «номером» я предполагаю то число, которое пойдет в выходной поток):
| Символ | Алфавит | Номер |
| р | абдкр | 4 |
| д | рабдк | 3 |
| а | драбк | 2 |
| к | адрбк | 4 |
| р | кадрб | 3 |
| а | ркадб | 2 |
| а | аркдб | 0 |
| а | аркдб | 0 |
| а | аркдб | 0 |
| б | аркдб | 4 |
| б | баркд | 0 |
Результатом будет последовательность
43243200040
На этом этапе не совсем понятно, какой прок от этого алгоритма. На самом деле, прок есть. Рассмотрим более абстрактную последовательность:
ааааббббеееееддддда
Для начала просто закодируем ее по методу Хаффмана. Для наглядности предположим, что расходы на хранения дерева при использовании перемещения стопки книг, и без оного совпадают.
Вероятности появления всех четырех символов в нашем случае равны ¼, то есть кодирование каждого символа требует 2 бит. Легко подсчитать, что кодированная строка займет 40 бит.
Теперь проведем изменение строки алгоритмом перемещения стопки книг. В начале алфавит имеет вид
M={а,б,д,е}.
После использования алгоритма строка будет иметь вид
10002000030000300003
В этом случае частоты появления символов сильно изменятся:
| Символ | Частота | Вероятность | Код Хаффмана |
| 0 | 15 | 3/4 | 0 |
| 3 | 3 | 3/20 | 10 |
| 2 | 1 | 1/20 | 110 |
| 1 | 1 | 1/20 | 111 |
В этом случае после кодирования мы получим последовательность в 15+6+3+3=27 бит, что намного меньше чем 40 бит, которые получаются без перемещения стопки книг.
Заключение
Итак, в этой статье были рассмотрены арифметическое кодирование, а так же алгоритмы преобразования, позволяющие получить более «удобный» для сжатия поток. Нужно отметить, что использование таких алгоритмов как BWT очень сильно зависит от входного потока. На эффективность влияют такие факторы, как лексиграфический порядок следования символов, направления обхода кодера (сжатие слева направо или справа налево), размер блока, и так далее. В следующей части статьи я рассмотрю какой-нибудь более сложный алгоритм, используемый в реальных кодерах (какой именно пока не решил).
Литература
- Ватолин Д., Ратушняк А., Смирнов М. Юкин В. Методы сжатия данных. Устройство архиваторов, сжатие изображений и видео; ISBN 5-86404-170-X; 2003 г.
- Лидовский В. В. Теория информации: Учебное пособие. – М.: Компания Спутник+, 2004.
- Семенюк В. В. Экономное кодирование дискретной информации. – СПб.: СПбГИТМО (ТУ), 2001.
- Witten I. H., Neal R. M., Cleary J. G. Arithmetic Coding for Data Compression, CACM, 1987.
Автор: Singerofthefall
