
Практически 10 лет и 50 статей назад, я набросал материал о моём знакомстве с замечательной системой компьютерной алгебры Maxima. Читать полностью »

Практически 10 лет и 50 статей назад, я набросал материал о моём знакомстве с замечательной системой компьютерной алгебры Maxima. Читать полностью »
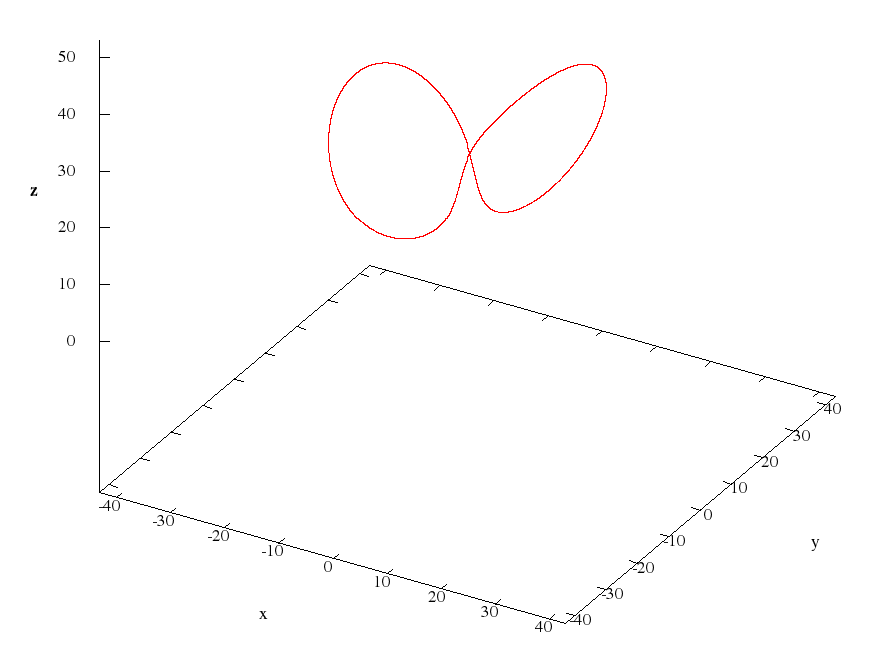
Этот топик продолжает серию моих статей на Хабре, посвященных исследованию аттрактора Лоренца.
Часть 1. Критический взгляд на аттрактор Лоренца
Часть 2. Динамическая система Лоренца и вычислительный эксперимент
Часть 3. О существовании периодических решений в системе Лоренца
Часть 4. Три цикла в аттракторе Лоренца
Итак, рассмотрим нелинейную систему дифференциальных уравнений, введенную Эдвардом Лоренцом в 1963 году:
где
классические значения параметров системы.Читать полностью »
В данном посте я хочу убить сразу нескольких зайцев во первых.
Еще раз Рассказать людям о свободной системе компьютерной алгебры. Maxima.
Во вторых найти вес «мистического зайца» из несложной задачки для школьников.
Таким образом прочитав, данную статью, вы узнаете, что такое Maxima, для каких целей её можно использовать, и как решить систему линейных уравнений в Maxima,
Maxima — свободная система компьютерный алгебры (Computer algebra system — CAS), основанная на Commmon Lisp. В своих функциональных возможностях она едва уступает другим современным платным CAS, таким как Mathcad, Mathematica, Maple; может проводить аналитические (символьные) вычисления, численные расчеты, строить графики (при помощи gnuplot). Имеется возможность написания скриптов и даже трансляции их в код на Common Lisp с последующей компиляцией. В виду того, что maxima писалась из разрабатывалась программистами lisp, ее синтаксис может показаться несколько запутанным, поскольку язык является сразу и императивным и функциональным. Я попытаюсь разъяснить именно эти моменты и доступно изложить суть функционального подхода, и совсем не буду акцентировать внимания на конкретных математических функциях: их довольно легко освоить самостоятельно. В данной статье рассматривается именно особенности исчисления и синтаксических конструкций maxima.Читать полностью »