Парадокс, положивший начало научным вычислениям

В 1953 году научные сотрудники Лос-Аламосской национальной лаборатории подбирали задачу для одного из первых электронных компьютеров. Выбор пал на простейшую одномерную систему — цепочку грузиков соединённых пружинами с нелинейной упругостью. Результаты моделирования вполне соответствовали ожиданиям: после возбуждения основного колебательного режима систему предоставляли самой себе, после чего энергия равномерно распределялась по остальным колебательным модам, и движения цепочки обретали характер белого шума.

Но однажды, из-за затянувшегося обеденного перерыва, машину оставили работать дольше обычного. Спохватившись, учёные вернулись в компьютерный зал и заметили, что расчётная система, пробыв некоторое время в состоянии теплового равновесия, вышла из него, а энергия в процессе эволюции периодично кочевала между наиболее длиноволновыми модами, практически не передаваясь на коротковолновые колебания. И в конце концов, система возвращалась из хаоса в исходное состояние! Этот парадокс ознаменовал собой рождение компьютерного моделирования, теории детерминированного хаоса и солитоники.

В своём предисловии к LOS ALAMOS-1940, которая была перепечатана в собрании сочинений Энрико Ферми в 1965 году, Станислав Улам писал, что Ферми давно был очарован фундаментальной загадкой статистической механики, которую физики называют «стрелой времени». Представьте себе съёмку столкновения двух бильярдных шаров: они катятся навстречу друг другу, сталкиваются и разлетаются в разные стороны. Теперь прокрутите плёнку в обратном направлении. Движение мячей выглядит совершенно естественно, и почему бы и нет: законы Ньютона, уравнения, управляющие движением шаров, одинаково хорошо работают как для положительного, так и для отрицательного направления времени. Теперь представьте себе начало игры в американский пул, где 15 шаров аккуратно сложены в треугольник, а кий стремительно отправляет в него биток, чтобы рассредоточить прицельные шары по всему столу. Если мы снимем столкновение и возникший хаос, никто из тех, кто когда-либо держал в руках бильярдный кий, не примет фильм, идущий вперёд, за фильм, идущий в обратном направлении: шары никогда не восстановят своё первоначальное треугольное расположение. Однако законы, управляющие всеми столкновениями, остаются теми же, что и в случае двух сталкивающихся бильярдных шаров. Что же придаёт стреле времени направление?

По причинам, которые мы рассмотрим ниже, Ферми считал, что ключевым моментом является нелинейность — отступление от простой ситуации, когда выход физической системы линейно пропорционален входу. Он знал, что найти решения нелинейных уравнений движения с помощью карандаша и бумаги будет слишком сложно. К счастью, поскольку он работал в Лос-Аламосе в начале 1950-х годов, у него был доступ к одному из самых ранних цифровых компьютеров. Учёные из Лос-Аламоса в шутку назвали его MANIAC (MAthematical Numerical Integrator And Computer). Он выполнял вычисления методом грубой силы, позволяя ученым решать задачи (в основном связанные с секретными исследованиями ядерного оружия), которые иначе были недоступны для анализа. Парадокс Ферми-Паста-Улама (ФПУ) был одним из первых не секретных научных исследований, проведённых с помощью MANIAC, и он положил начало эпохе того, что иногда называют экспериментальной математикой.

Словосочетание «экспериментальная математика» может показаться оксюмороном: всем известно, что достоверность математики не зависит от того, что происходит в физическом мире. Тем не менее, оригинальное исследование ФПУ можно с полным основанием назвать рождением экспериментальной математики, под которой мы понимаем компьютерные исследования, разработанные для того, чтобы дать понимание сложных математических и физических проблем, которые недоступны, по крайней мере, на начальном этапе, с помощью более традиционных форм анализа.

В настоящее время вычислительные исследования сложных (как правило, нелинейных) задач столь же обыденны, сколь и необходимы, а компьютер занял достойное место наряду с физическим экспериментом и теоретическим анализом в качестве инструмента для изучения множества явлений в естественных, технических и математических науках. Строгие математические доказательства, такие как доказательство знаменитой "задачи о четырёх красках", теперь проводятся с помощью компьютеров. В гидродинамике компьютерные визуализации сложных, зависящих от времени потоков имеют решающее значение для выявления глубинных физических механизмов. Современные эксперименты в физике конденсированного вещества, наблюдения в астрофизике и данные в биоинформатике было бы невозможно интерпретировать без компьютеров. Со времени первого эксперимента ФПУ прошло много лет, и в этом свете становится особенно важно понять, как разворачивалась их новаторская работа.

Вместе с Джоном Паста и Уламом, Ферми предложил исследовать, как он предполагал, очень простую нелинейную динамическую систему — цепь точечных масс, соединённых пружинами, для которой движение разрешено только вдоль линии цепи. Идеализированный набор масс и пружин не испытывал трения или внутреннего нагрева, поэтому они могли колебаться вечно без потери энергии. Однако пружины этой теоретической системы были не из тех, что изучают на вводных курсах физики: создаваемая ими восстанавливающая сила не была линейно пропорциональна величине сжатия или растяжения. Вместо этого в математическую зависимость были включены нелинейные компоненты между величиной деформации и результирующей восстанавливающей силой.

Ферми, Паста и Улам смоделировали серию масс, соединённых друг с другом пружинами. Массы движутся вперёд и назад согласно закону движения Ньютона f = ma (сила равна массе, умноженной на ускорение) вдоль соединяющей их линии. Здесь соответствующие силы — это восстанавливающие силы, приложенные пружинами. Новизна и увлекательность исследования заключается в том, что восстанавливающие силы нелинейно зависели от степени сжатия или растяжения пружины.

Ключевой вопрос интересующий исследователей заключался в том, сколько времени потребуется колебаниям нелинейных пружин, чтобы прийти к равновесию. Равновесие, которого они ожидали, аналогично состоянию теплового равновесия в газе. В одноатомном газе, таком как гелий, тепловая (кинетическая) энергия молекул при равновесии равномерно распределяется между тремя возможными компонентами движения, которые они могут иметь: вдоль осей x, y или z. Например, не будет существенного различия в количестве атомов прыгающих вверх-вниз и прыгающих влево-вправо.

Это понятие равномерного распределения энергии между различными способами движения является основополагающим. Это предписание, известное как теорема статистической механики о равнораспределении, можно применить к молекулам более сложным, чем похожий на бильярдный шар гелий, и способным распределять энергию между вращательными или колебательными движениями (Vibration of Molecules CHEM Study — хорошее видео для понимания (ком. перев.) ). Применение теоремы о равнораспределении позволяет физикам рассчитывать такие вещи, как теплоемкость газа, на основе базовой теории.

Для начала система была запущена в одном простом режиме колебаний. Если бы системой была цепочка линейных пружин (без демпфирующих сил), то этот один режим сохранялся бы бесконечно. Однако при использовании нелинейных пружин могут возбуждаться различные режимы колебаний. Учёные ожидали, что со временем система «термализуется»: колеблющиеся массы распределят свою энергию поровну между всеми различными режимами колебаний, которые возможны для этой системы.

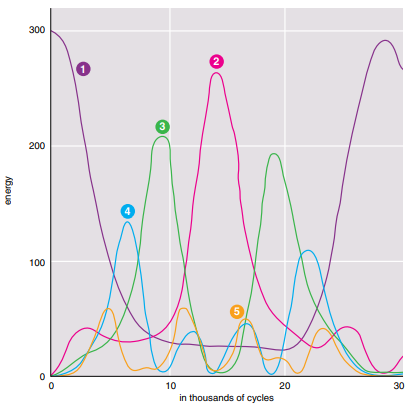
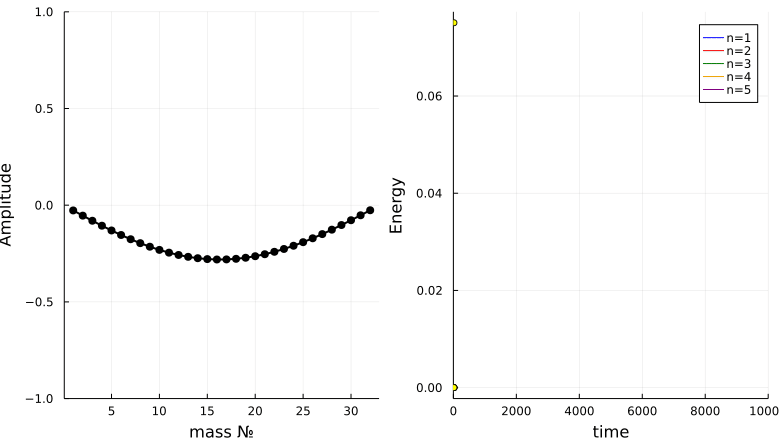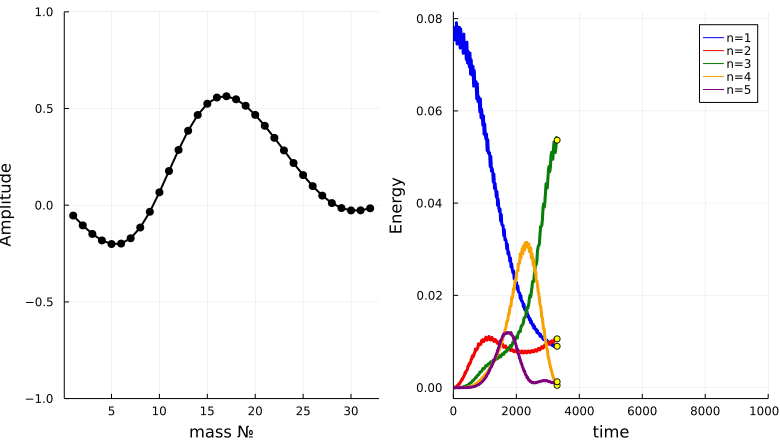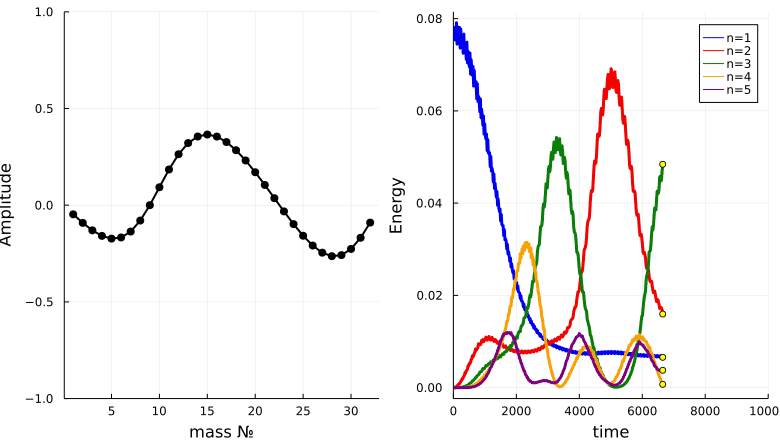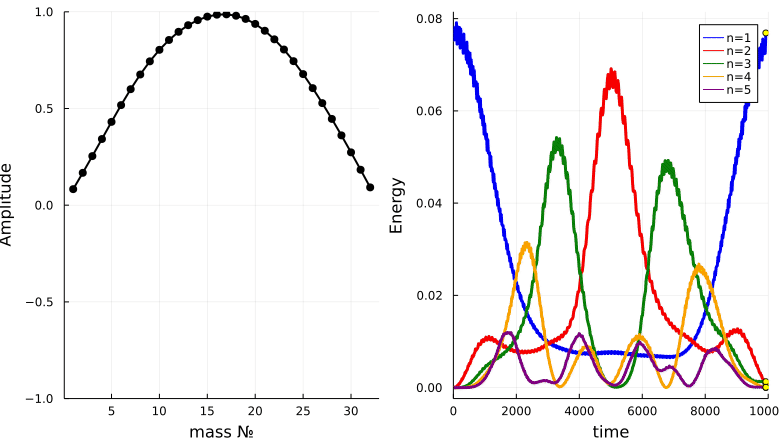
Ферми, Паста и Улам инициализировали систему задав энергию только в самой низкой моде колебаний (1) и рассчитали, что из этого получится. Они ожидали, что в конечном счёте энергия будет распределена поровну между всеми возможными режимами. Вместо этого они обнаружили, что после распределения между несколькими модами низкого порядка, очень большая часть энергии позже возвращается в режим, который они использовали для инициализации системы. (Цвета соответствуют аналогичным режимам, показанным на следующем рисунке) Это наблюдение, которое они скромно назвали «маленьким открытием», ознаменовало рождение экспериментальной математики

Визуализация возможных мод колебаний немного сложна для цепочки масс, но легко увидеть возникновение различных колебательных режимов, например, в струне скрипки. Один лад соответствует основному тону, в котором смещение струны максимально в центре и уменьшается по мере приближения к её закреплённым концам. Другой лад — первый гармонический (на октаву выше), при котором одна половина струны движется вверх, а другая — вниз, и так далее. Вибрирующая струна имеет бесконечное число мод, но система ФПУ — конечное (равное числу присутствующих масс).

Ферми, Паста и Улам ожидали, что энергия в их системе «масса-пружина» в итоге будет распределена поровну между различными модами движения, которые аналогичны модам вибрации струны скрипки. Основная мода колебаний такой струны (фиолетовая) соответствует слышимой ноте. Более высокочастотные колебания порождают различные гармоники этой ноты. Показанные здесь движения соответствуют второй (розовой), третьей (зелёной), четвёртой (синей) и пятой (оранжевой) гармоникам.

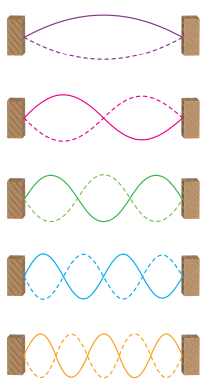
Для проведения своего исследования ФПУ (вместе с Мэри Цингу, которая, хотя и не является автором отчёта, внесла значительный вклад в работу) рассмотрели различные количества масс (16, 32 или 64) в своих вычислительных экспериментах. Затем они численно решили связанные нелинейные уравнения, которые управляют движением масс. (Они могли легко вывести эти уравнения из нелинейной функции пружины и известного закона Ньютона f = ma.) Учёные задали MANIAC'у время, соответствующее большому количеству периодов основного режима. Они были совершенно ошеломлены результатами. Первоначально энергия распределялась между несколькими различными режимами. По истечении большего (смоделированного) времени их система вернулась в состояние, напоминающее исходное. Действительно, 97 процентов энергии в системе в конечном счёте было восстановлено в том режиме, который они изначально установили. Словно по волшебству бильярдные шары собрались из своего разрозненного состояния в идеальный исходный треугольник!

Конечно, не всех убедили эти расчёты. Одним из популярных предположений было то, что ФПУ недостаточно долго проводили моделирование — или, возможно, время, необходимое для достижения равнораспределения для системы FPU, было просто слишком большим для численного наблюдения. Однако в 1972 году физик из Лос-Аламоса Джеймс Л. Тук и Цингоу (которая к тому времени использовала свою супружескую фамилию Мензел) развеяли эти сомнения, проведя чрезвычайно сложное численное моделирование, которое обнаружило повторения на таких удивительно длинных временных масштабах, что их иногда называют «суперповторениями». Это исследование позволило понять, что термализация энергии не была скрыта от ФПУ слишком короткими компьютерными симуляциями — на самом деле происходило нечто более интересное.

▍ 1 + 1 = 3

Почему Ферми решил, что нелинейные пружины обеспечат равнораспределение энергии в этом эксперименте? И что это вообще за странная концепция нелинейности? Очевидно, что этот термин противопоставляется линейности, которую мы до сих пор обсуждали только с точки зрения пропорциональности входа и выхода.

Студенты-физики изучают линейные системы на вводных занятиях, потому что их гораздо легче анализировать и понимать. Когда точечную массу соединяют с линейной пружиной и дают ей толчок, её последующее поведение очень простое: она будет колебаться вперёд-назад на резонансной частоте системы, которая зависит только от величины массы и постоянной упругости (коэффициент, связывающий величину растяжения или сжатия с восстанавливающей силой). Однако с нелинейной пружиной всё гораздо сложнее. Например, частота колебаний зависит от амплитуды. Слегка подтолкните грузик, и он будет колебаться с одной частотой; сильно пните его, и он начнёт колебаться с другой. Когда человек впервые изучает физику, у него легко может сложиться впечатление, что нелинейные системы являются аномальными. Но нелинейные взаимодействия на самом деле гораздо более характерны для реального мира, чем линейные. По этой причине физики, как известно, язвили, что термин «нелинейная наука» имеет столько же смысла, сколько «неслоновая зоология» (шутка, которую иногда, ошибочно, приписывают Уламу).

Чем нелинейные системы отличаются от линейных, кроме того, что имеют зависящие от амплитуды частоты колебаний? В линейной системе удвоение амплитуды входного сигнала приводит к удвоению амплитуды выходного сигнала, как мы уже обсуждали. Предположим, кто-то поёт в два раза громче в микрофон в караоке-клубе — усиленное пение будет в два раза громче, когда оно будет выходить из колонок. Аналогично, если два человека поют дуэтом, результат будет просто суммой (или «суперпозицией») того, что получилось бы, если бы каждый пел свою партию отдельно. Кроме того, если всё действительно линейно, голоса не будут искажаться. Частоты, которые выходят (то есть, ноты, которые слышны), будут именно теми, которые дуэт ввёл, независимо от амплитуды.

С нелинейными системами всё гораздо сложнее. Например, принцип суперпозиции не действует. Кроме того, выходные частоты не ограничиваются входными частотами. Например, крик в микрофон караоке может перегрузить усилитель, заставив его перейти в нелинейный режим. То, что выходит из динамиков, сильно искажается и содержит частоты, которые никогда не пелись. Могут иметь место и гораздо более тонкие эффекты.

Один из тонких эффектов нелинейной физики был впервые замечен в 1830-х годах, когда молодой инженер по имени Джон Скотт Рассел был нанят для изучения вопроса о том, как повысить эффективность конструкций барж для канала Юнион вблизи Эдинбурга, Шотландия. По счастливой случайности трос, тянущий баржу, дал трещину. Рассел описал, что после этого произошло:

Я наблюдал за движением лодки, которую пара лошадей быстро тащила по узкому каналу, когда лодка внезапно остановилась — не так, как масса воды в канале, которую она привела в движение; она скапливалась вокруг носа судна в состоянии сильного волнения, затем внезапно оставляя его позади, покатилась вперёд с большой скоростью, принимая форму большого одиночного возвышения, округлого, гладкого и чётко очерченного холма воды, который продолжал свой путь по каналу, по-видимому, без изменения формы или уменьшения скорости. Я последовал за ним верхом и нагнал его, всё еще движущегося со скоростью восемь-девять миль (14 км) в час, сохраняя свою первоначальную фигуру длиной около тридцати футов и высотой от фута до полутора футов. Его высота постепенно уменьшалась, и после погони в одну-две мили (3 км) я потерял его в извивах канала.

Эта странная волна вела себя не так, как обычная волна на поверхности океана. Волны на море (и многие другие знакомые виды волн) движутся со скоростью, зависящей от длины их волн. Это явление называется дисперсией. Возмущение, подобное тому, которое возникло перед баржей Рассела, можно представить как суперпозицию чисто синусоидальных волн, каждая из которых имеет свою длину волны. Однако если на поверхности открытого океана образуется компактное возмущение, то каждая из составляющих его волн будет двигаться с разной скоростью. В результате начальное возмущение не сохранит свою форму. Вместо этого такая волна станет растянутой и искажённой.

Обладая пытливым умом, Рассел продолжил своё случайное открытие с помощью контролируемых лабораторных экспериментов и количественно описал открытое им явление в публикации 1844 года. Там он показал, например, что уединённые волны большой амплитуды в канале движутся быстрее, чем малые — нелинейный эффект.

В 1830-х годах инженер Джон Скотт Рассел наблюдал странную волну на Юнион-канале в Шотландии, которая не рассеивалась обычным образом, а сохраняла свою форму по мере продвижения по каналу. Потребовалось более века, чтобы это явление было понято как результат нелинейных эффектов, компенсирующих ожидаемую дисперсию. Один из авторов (Забуски) и покойный Мартин Крускал придумали термин солитон для описания такой волны, которая может возникать в различных физических системах. На этой фотографии 1995 года изображена частично успешная попытка воссоздать волну Рассела на канале Юнион. (Фотография любезно предоставлена Крисом Эйлбеком, Университет Хериот-Ватт).

В 1895 году голландский физик Дидерик Кортевег и его студент Густав де Врис (де Фриз) вывели нелинейное дифференциальное уравнение, известное сегодня как уравнение Кортевега-де Фриза (КдФ), которое, по их мнению, может описать результаты экспериментов Рассела. Это уравнение показывает, что скорость изменения во времени высоты волны определяется суммой двух членов: нелинейного (который приводит к амплитудно-зависимым скоростям) и линейного (который вызывает дисперсию, зависящую от длины волны). В частности, Кортевег и де Фриз нашли решение для одиночной волны, которое соответствовало странной волне, за которой Рассел следовал верхом на лошади. Это решение возникает в результате баланса между нелинейностью и дисперсией. Голландские физики также нашли периодическое решение своего уравнения, но они не смогли получить общие решения.

Их работа и наблюдения Рассела канули в безвестность и были проигнорированы математиками, физиками и инженерами, изучающими водные волны, до начала 1960-х годов, когда один из авторов данной статьи (Забуски) и ныне покойный Мартин Крускал из Принстонского университета приступили к изучению цепочки ФПУ. Они начали с классической модели ФПУ, но использовали, по сути, бесконечно малые пружины и массы, чтобы представить непрерывную линию деформируемого материала, а не серию дискретных масс. Этот подход позволил им изучить ситуации с большими длинами волн и получить дифференциальное уравнение, которое соответствовало обычному уравнению, описывающему линейные волны, за исключением изменённой дисперсии. Чтобы представить прогрессирующие волны в системе, Крускал вывел из этого уравнения то, что он и Забуски позже признали как уравнение КдФ. Это казалось неразрешимой аналитической задачей, поэтому они (с помощью Гэри Дима, который в то время работал в Bell Telephone Laboratories) использовали численное моделирование, чтобы наблюдать почти полное повторение начальных условий. Для описания своих решений уравнения КдФ они придумали термин, который стал широко использоваться для обозначения явления уединённой волны: солитон.

На реке Северн в Англии можно заниматься сёрфингом, поскольку широкое устье периодически направляет исключительно высокие паводковые приливы вверх по реке, образуя так называемые приливные боры. Волны, которые следуют за начальным натиском, сохраняют свою форму на протяжении многих километров, позволяя совершать рекордные заезды для сёрфинга. Такие недисперсионные волны возникают во многих физических системах, включая, казалось бы, простую систему масс и пружин

Они обнаружили, что солитоны развиваются из начального состояния и затем перемещаются влево и вправо, пока не поменяют свои относительные позиции и не сфокусируются почти точно в другой точке пространства. Эта работа (и работа многих последующих исследователей) способствовала огромному количеству аналитических, теоретических и экспериментальных достижений в огромном количестве областей математики и физики.

Система, подобная той, которую моделировали Ферми, Паста и Улам, но с 256 массами (слева), легко порождает солитоны, которые могут распространяться в любом направлении, обмениваться позициями и в конечном счёте возвращать систему к чему-то, напоминающему её начальную конфигурацию. Движение солитонов здесь можно увидеть, следуя линиям горячего цвета, которые обозначают большие смещения масс. Горизонтальная ось соответствует положению вдоль ряда пружин и масс. Вертикальная ось соответствует времени, которое начинается снизу и продвигается вверх. Возникновение распространяющихся солитонов не требует, чтобы массы были дискретными: они также возникают в непрерывном аналоге системы ФПУ (справа)

Пока Забуски, Крускал и Дим были заняты проблемой ФПУ, японский математический физик Морикадзу Тода исследовал похожую нелинейную систему и математически доказал, что в ней никогда не может быть хаоса. В цепочке ФПУ явно было что-то особенно тонкое.

▍ Приспешники Хаоса?

Уединённые волны действительно могут создавать удивительно регулярное поведение, но движение системы ФПУ также может быть довольно хаотичным. Действительно, даже очень простые динамические системы обычно поддерживают сложную смесь регулярного и хаотического поведения.

Здесь мы используем слово "хаотичный" в его научном смысле. Мы не имеем в виду случайность. Исход в задаче ФПУ регулируется законами Ньютона, которые точно определяют всё будущее движение — здесь нет случайных событий. Однако через некоторое время движения действительно могут показаться очень беспорядочными и неустойчивыми. Более того, состояние системы пружин и масс ФПУ через определённое время очень чувствительно к её начальной настройке: измените хоть немного начальные условия, и через некоторое время результат будет совершенно другим. Многие системы, включая атмосферные колебания, которые приводят к изменению погоды, демонстрируют это свойство и поэтому считаются хаотичными, даже если их движение в течение короткого периода времени может казаться достаточно регулярным. На самом деле, как показывает сама проблема ФПУ, движение в течение даже очень длительных периодов времени может быть довольно регулярным!

Чтобы определить, является ли движение данной системы регулярным или хаотичным (при определённых начальных условиях) в долгосрочной перспективе, полезно построить график изменения конфигурации системы во времени. Проблема в том, что даже простая на первый взгляд динамическая система, состоящая всего лишь из одной массы, имеет шесть переменных для построения графика: координаты и скорости в x, y и z.

Построение всех шести значений для точечной массы в зависимости от времени обычно приводит к визуальному беспорядку, который очень трудно интерпретировать. Однако, построение графика с разумным выбором подмножества точек (которые удовлетворяют определённому, физически мотивированному условию, например, когда определённая переменная скорости равна нулю) облегчает интерпретацию происходящего. Такие участки называются отрезками Пуанкаре, в честь французского физика и математика Жюля Анри Пуанкаре.

Регулярные траектории так же предсказуемы, как орбиты планет вокруг Солнца или распорядок дня жителя пригорода. Они могут быть отслежены во времени с большой точностью. С другой стороны, хаотические траектории крайне нерегулярны. Они склонны блуждать, как пьяные матросы, и ограничены только количеством доступной им энергии. Хаос важен для проблемы ФПУ, поскольку, если он достаточно силен, он будет перемешивать энергию между модами колебаний. То есть, хаос может привести к разделению энергии в такой системе. Хотя ни ФПУ, ни Тук и Мензел не обнаружили равнораспределения, в своём исследовании 1967 года Забуски и Дим сделали это, проведя моделирование системы ФПУ, для которой начальные движения масс имели короткую длину волны большой амплитуды. К 2006 году другие исследователи подтвердили это равенство с помощью более комплексного моделирования и анализа.

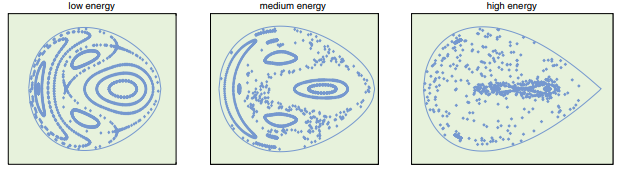
Хаотические взаимодействия помогли бы привести к разделению энергии, которое ожидали увидеть Ферми, Паста и Улам. Но эти исследователи не вкладывали в свою систему достаточно энергии, чтобы привести к равнораспределению. Связь с хаосом можно проиллюстрировать на примере системы, математически эквивалентной трехмассовой цепи ФПУ, которую астрономы Мишель Энон и Карл Хайлес изучали в 1963 году. Поведение системы Энона-Хейлеса лучше всего рассматривать с помощью графиков Пуанкаре, которые показывают точки пересечения многомерных траекторий системы с одной выбранной плоскостью. Увеличение энергии в системе дает прогрессию от регулярных траекторий (слева), к траекториям, которые отражают как регулярное, так и хаотическое поведение (в середине), и к траекториям, которые в основном хаотичны (справа).

Основываясь на исследованиях хаоса и равнораспределения, проведенных в конце 1960-х годов Борисом Чириковым, Эдди Коэн из Рокфеллеровского университета и несколько его коллег недавно исследовали систему ФПУ при высоких энергиях. Исследуя этот вопрос систематически, они продемонстрировали существование двух порогов (как функции энергии на осциллятор) в динамике системы ФПУ. На первом пороге движение переходит от полностью регулярного к слабо хаотическому — есть некоторое хаотическое поведение, но в подавляющем большинстве случаев всё остаётся очень регулярным. При превышении второго, более высокого порога возникает сильный хаос, позволяющий быстро распределять энергию между режимами.

Коэн и соавторы также обнаружили, что термализация происходит быстрее, когда масс больше. Когда число нелинейных осцилляторов становится бесконечным (то есть в реальных ситуациях, которые пытались смоделировать ФПУ), равнораспределение действительно возникает для любого уровня вводимой энергии. Начальные условия, которые ФПУ использовали в своих численных симуляциях, были, однако, ниже порога хаоса, что не позволило им увидеть равнораспределение энергии между различными режимами колебаний. Троица из Лос Аламоса могла бы наблюдать это равенство, если бы использовала либо более высокие значения нелинейности (дающие более сильное взаимодействие между различными модами), либо начальные импульсы с большей энергией. Мы должны быть благодарны за то, что они этого не сделали, учитывая, сколько интереса и понимания возникло в результате.

Один из примеров можно увидеть в исследованиях теплопроводности. (Тема теплопроводности была ключевым мотивом для исследования ФПУ). В начале 19 века французский математик Ж. Б. Жозеф Фурье ввёл простой феноменологический закон для описания потока тепла в твёрдых телах. Однако за два столетия, прошедших с тех пор, учёные так и не смогли вывести этот закон напрямую, используя первые принципы. Попытки сделать это предпринимались еще в 1914 году, когда Петер Дебай изучал теплопроводность в диэлектрических кристаллах. Он предположил, что конечная проводимость таких кристаллов возникает из-за нелинейных взаимодействий в колебаниях их решётки — именно то явление, для исследования которого был разработан подход ФПУ.

С тех пор было проделано много работы по изучению теплопроводности с использованием моделей, подобных ФПУ, в которых каждый конец цепи заземлён на «тепловой ванне» (один конец горячий, а другой холодный), а каждая точечная масса испытывает силы в дополнение к тем, которые исходят от её соседей. Например, эти модели использовались для изучения того, как теплопроводность зависит от количества масс и степени хаоса в системе. Хотя было получено много важных выводов, полный набор необходимых и достаточных условий для справедливости закона Фурье остается неизвестным. Физики были бы очень рады разрешить эту неловкую ситуацию.

▍Каждый твой вздох

Спустя десятилетия парадокс ФПУ продолжает вдохновлять на изучение многих других увлекательных нелинейных систем, таких как атомные решётки в физике твёрдого тела. До конца 1980-х годов считалось само собой разумеющимся, что колебания этих решёток должны распространяться на расстояния, которые очень велики по сравнению с расстоянием между атомами. Единственными признанными исключениями были те, которые возникали из-за дефектов, разрушающих регулярное расположение атомов в решётке — например, из-за загрязнений или нарушений в чистом кристалле. Принято считать, что только такие неровности могут вызвать локализацию вибраций (хотя более ранние работы Забуски и Дима намекали на обратное).

Эта перспектива была вывернута наизнанку открытием локализованных мод колебаний в идеальных решётках. Такие моды, известные как внутренние локализованные моды (ВЛМ) или дискретные бризеры, могут возникать в сильно нелинейных, пространственно протяжённых решётках и (грубо говоря) играют роль, аналогичную солитонам в непрерывных физических системах. Однако, в отличие от солитонов, ВЛМ не нужно распространяться: они могут просто вибрировать на месте. В настоящее время физики экспериментально наблюдают бризеры в различных физических системах, включая твёрдые тела с переносом заряда, решётки джозефсоновских переходов, фотонные кристаллы, решётки микромеханических осцилляторов и конденсаты Бозе-Эйнштейна.

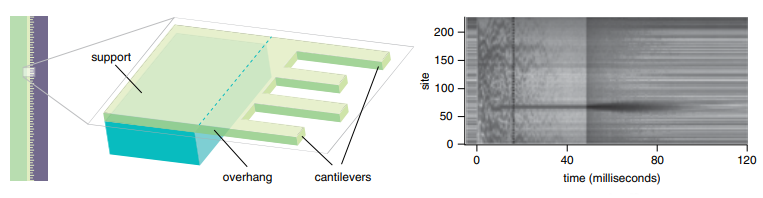
В течение многих лет физики считали, что колебания регулярной решётки, скажем, атомов в идеальном кристалле, должны быть распределены в пространстве. Но в конце 1980-х годов физики и математики поняли, что нелинейные системы могут поддерживать пространственно локализованные колебания. Такие внутренние локализованные моды или дискретные бризеры с тех пор наблюдались экспериментально в ряде физических систем. Одна из таких систем состоит из ряда микромеханических балок (слева). Вибрация луча вызывает уменьшение отражаемого им света, как видно на изображении (справа), где прослеживается эволюция системы. Через несколько десятков миллисекунд вибрация становится локализованной в массиве лучей, что приводит к появлению тёмной горизонтальной линии

Как нелинейность может вызвать локализованный режим колебаний в решётке? Чтобы понять это, рассмотрим два нелинейных осциллятора, которые могут слабо взаимодействовать. Напомним, что поскольку эти осцилляторы нелинейны, частота их колебаний зависит от их энергии. Представьте, что один осциллятор запускается сильным возбуждением, а другой — слабым, так что большая часть энергии системы сначала локализована в первом осцилляторе. В принципе, можно выбрать эти начальные возбуждения так, чтобы их колебания были несоизмеримы (что делает отношение частот их колебаний иррациональным числом).

Следовательно, после запуска обоих осцилляторов на максимальной амплитуде они никогда больше не синхронизируются. Это не позволяет колебаниям первого осциллятора (или любой из его гармоник) резонировать с любой из мод второго осциллятора, что очень затрудняет передачу энергии между двумя осцилляторами.

Теперь рассмотрим цепочку с большим количеством осцилляторов. Установим, что один из них вибрирует с относительно большой амплитудой и с частотой, несоизмеримой с частотой меньших колебаний, которые совершают другие осцилляторы. Этот особый осциллятор теперь с трудом передаёт энергию своим соседям. Таким образом, этот осциллятор и, возможно, небольшое число соседних поддерживают колебания большой амплитуды в течение длительного времени, создавая ВЛМ.

В 1988 году Альберт Сиверс (Корнельский университет) и Шозо Такено (Киотский технический университет) показали, что бризеры могут возникать в решётке ФПУ. Эта идея продолжает активно реализовываться и привела к новым интересным разработкам. В частности, в серии работ, начиная с 2005 года, Сергей Флач из Института физики сложных систем имени Макса Планка и его коллеги использовали эту перспективу, чтобы по-новому взглянуть на рекуррентность ФПУ, которая, по их мнению, является результатом существования объектов, называемых q-бризерами. Одной из наиболее активных исследовательских проблем в нелинейной науке является согласование подхода Флаха к пониманию динамики ФПУ с более ранней солитонной перспективой.

▍ Где-то там, за радугой...

Как мы уже обсуждали в мельчайших подробностях, многие очень умные люди за последние полвека проделали значительный путь в многочисленных исследованиях парадокса ФПУ и связанных с ним систем. В ходе этого процесса такие понятия, как хаос, солитоны и бризеры, были изобретены, разработаны, уточнены и применены к ряду реальных систем.

Задача ФПУ затрагивает удивительно широкий спектр тем в нелинейной динамике, статистической механике и вычислительной физике. Тем не менее, эти широкие категории представляют собой лишь малую часть научной литературы, порождённой оригинальным исследованием. Новые статьи по парадоксу ФПУ публикуются и сегодня, спустя 65 лет после первоначального отчёта из Лос-Аламоса. Мы вполне ожидаем, что работа такого рода будет занимать исследователей еще долго после того, как учёные отпразднуют столетие проблемы Ферми-Паста-Улама в 2055 году.

❒ Приложение

В дополнение к переводу хотелось бы добавить немного теории. Гамильтониан цепочки нелинейных осцилляторов имеет вид:

Сумма потенциальной и кинетической энергий. Пружинки подчиняются закону Гука с небольшими нелинейными поправками. При α = β = 0 будет обычная линейная связь, которую проходят в школе и на младших курсах, случай β = 0 носит название α-ФПУ, и, соответственно, при α = 0 будет β-ФПУ. Для последних двух случаев можно записать уравнения движения:

Дальше обычно осуществляется преобразование к нормальным модам, но и в таком виде эти дифуры вполне решаемы. К слову, α-ФПУ при переходе к непрерывному случаю образует уравнение КдФ, а из β-ФПУ можно получить одномерное нелинейное уравнение Шрёдингера (The Fermi-Pasta-Ulam problem: 50 years of progress 2005, The limit of stochasticity for a one-dimensional chain of interacting oscillators 1984). И нелинейная природа этих уравнений порождает солитоны.

Для решения системы из 64 дифуров (по два на каждый грузик) будем использовать код на Julia:

using Plots, FFTW
cd(s"C:UsersUserDesktopMycopplots")

function rk4(f, x, y, h)
    k1 = h * f(x       , y        )
    k2 = h * f(x + 0.5h, y + 0.5k1)
    k3 = h * f(x + 0.5h, y + 0.5k2)
    k4 = h * f(x +    h, y +    k3)

    return y + (k1 + 2*(k2 + k3) + k4)/6.0
end;

function fpu_problem(;N=32, points = 256, 
    				tmax = 10000, dt = 1, α = 0.25)

    a=1
    tspan = range(0, stop = tmax, step = dt)
    Nt = length(tspan)
    tcut = Nt ÷ points # на графики не все моменты t
    tscaled = tcut:tcut:Nt
    U0 = [ a*sin(π*i/(N+1)) for i = 1:N ]
    U0 = [U0; zeros(N)] # начальные условия
    du = zeros(2N)
    
    function fpu(t,u)
        du[1] = u[N+1]
        du[N] = u[2N]
        du[N+1] = u[2]-2u[1] + α*( (u[2]-u[1])^2-u[1]^2 )
        du[2N] = u[N-1] - 2u[N] + α*( u[N]^2-(u[N]-u[N-1])^2 )
        
        for i = 2:N-1
           du[N+i] = u[i+1] + u[i-1] - 2u[i] + 
      		α*( (u[i+1]-u[i])^2-(u[i]-u[i-1])^2 )
           du[i] = u[N+i]
        end
        return du
    end
    XY = [ U0 = rk4(fpu, t, U0, step(tspan)) for t in tspan ]
    tspan[tscaled], XY[tscaled]
end

@time T, XY = fpu_problem(N=32, points=512, tmax=10000, dt=0.1);

anim = @animate for i ∈ 1:16:length(XY)
    plot( XY[i][1:32], m = (5, :black), ylim = (-1,1), title="$i",
        legend = false, line = (2, :black) )
end
gif(anim, "fpu.gif", fps = 2)

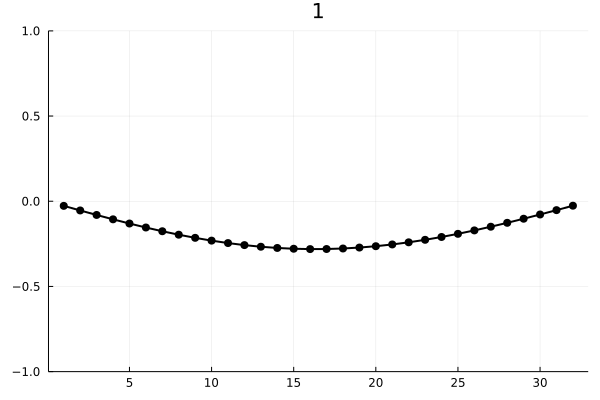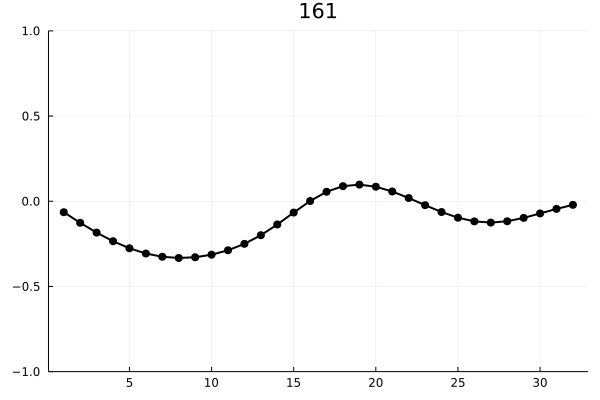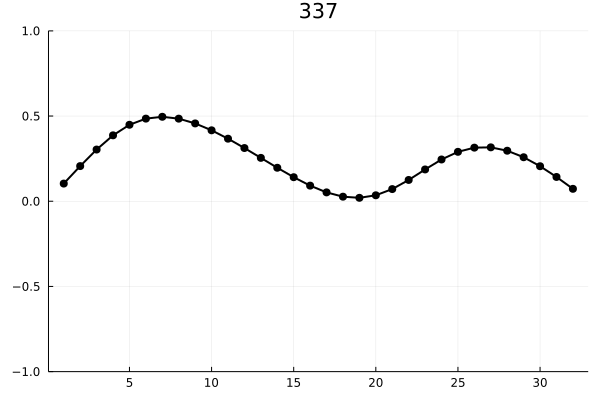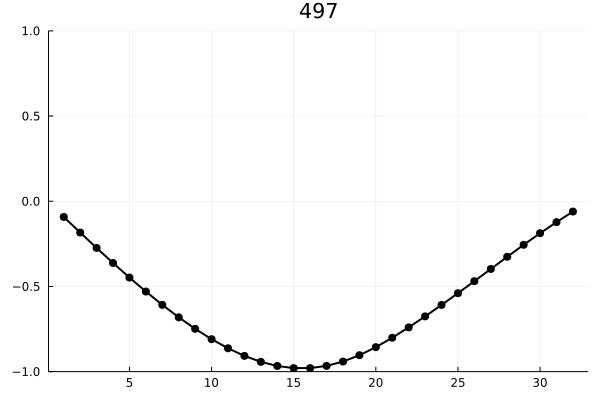
И визуализируем энергию первых пяти мод:

N = 32
omegak2 = [ 4*(sin(0.5π*i/N))^2 for i = 1:N ]# Mode Frequencies
Energ = zeros(length(XY), N);

for i = 1:length(XY)
   YX = [0; XY[i][1:N]]  
   YV = [0; XY[i][N+1:2N ]]
   sXF = imag( fft( [ YX; 0; -YX[N+1:-1:2] ] ) ) / sqrt(2*(N+1)) 
   sVF = imag( fft( [ YV; 0; -YV[N+1:-1:2] ] ) ) / sqrt(2*(N+1))
   Energ[i,:] .= 0.5*( omegak2[1:N].*(sXF[2:N+1].^2)+sVF[2:N+1].^2 ) 
end

 plot(T,Energ[:,1], line = (3, :blue), lab = "n=1")
plot!(T,Energ[:,2], line = (3, :red), lab = "n=2")
plot!(T,Energ[:,3], line = (3, :green), lab = "n=3")
plot!(T,Energ[:,4], line = (3, :orange), lab = "n=4")
plot!(T,Energ[:,5], line = (3, :purple), lab = "n=5")
xaxis!("time")
yaxis!("Energy")

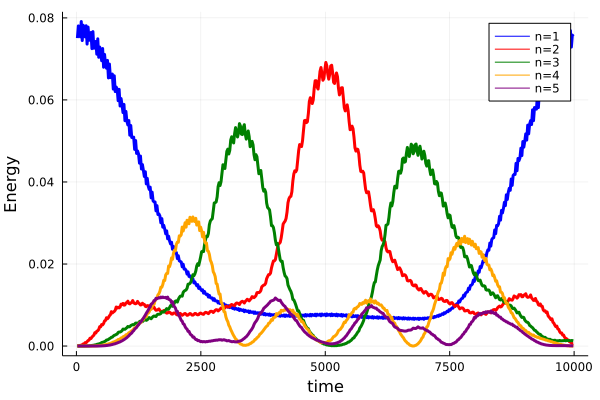
Расчёт занимает меньше секунды, и это я еще не заморочился избавиться от лишних аллокаций и подсчётов. Теперь не то что пообедать — зевнуть не успеть, пока ждёшь результата. Да и использование метода с фиксированным шагом есть расточительство оправдываемое только простотой кода. У себя на компьютере можно ставить количество фреймов и fps побольше, тогда анимации будут красивей, а здесь используются дёрганные, но легковесные файлы.

▍ Материалы для погружения в тему

• Кажется, эта квантовая машина противоречит стремлению Вселенной к беспорядку
• Математики решили проблему Ферми-Паста-Улама
• Russian scientists have discovered a new physical paradox (перевод)
• Как из хаоса рождается порядок? [Veritasium]
• Учёные обнаружили новые экзотические формы синхронизации